卡特兰数
优秀博客
卡特兰数是一种经典的组合数,经常出现在各种计算中,其前几项为 : 1, 2, 5, 14, 42,132, 429, 1430, 4862, 16796,
如果打表or手模找到如上规律可考虑卡特兰数
公式1:
(Catalan(n)=sum_{i=0}^{n-1}{Catalan(i)*Catalan(n-i-1)})

进出栈问题
QUESTION : 一个足够大的栈的进栈序列为1,2,3,⋯,n时有多少个不同的出栈序列?
f[i]表示i个数的全部可能性。
f[0] = 1, f[1] = 1; 设 x 为当前出栈序列的最后一个,则x有n种取值
由于x是最后一个出栈的,所以可以将已经出栈的数分成两部分
- 比x小 2.比x大
比x小的数有x-1个,所以这些数的全部出栈可能为f[x-1]
比x大的数有n-x个,所以这些数的全部出栈可能为f[n-x]
这两部分互相影响,所以一个x的取值能够得到的所有可能性为f[x-1] * f[n-x]
另外,由于x有n个取值,所以
公式2:
(ans = f[0]*f[n-1] + f[1]*f[n-2] + ... + f[n-1]*f[0];)
同理解释公式1 :考虑最后一个出栈的元素,比其先进栈先出栈的元素有i个,则比其后进栈先出栈的元素有n−i−1
球迷购票问题
法1:dp
必须先有 50 元,才能收 100 元(每收一个 100 就得找出一个 50),所以我们枚举手头 50 元的张数就行了。
$ dp[ i ][ j ] $表示考虑到了前 i 个人,手里现有 j 张 50 。(0<=j<=i)
每一个$ dp[ i ][ j ] $可以由上一个拿了 50 或者 100 转移过来。
拿了 100 就是 $ dp[i-1][j-1] $,(拿了 100 自然就得找出一张 50,所以是 j-1)那拿了 50 就自然是 $ dp[i-1][j+1] $了(手头多了一张 50)
#include <cstdio>
#include <iostream>
using namespace std;
long long f[5050][50];
int n;
int main(){
scanf("%d",&n);
f[0][0]=1;
for(int i=1;i<=n*2;i++)
for(int j=0;j<=min(i,n);j++){
if(j-1>=0)f[i][j]+=f[i-1][j-1];
if(j+1<=i+1)f[i][j]+=f[i-1][j+1];
}
printf("%lld
",f[n+n][0]);
return 0;
}
法2:
一个A买票后售票处会积累50元钱,一个B买票需要售票处找零50元钱
说明在一个B买票前至少需要一个A买过票,那么我们就可以将A看作左括号,B看作右括号
问题就是要求合法得括号匹配,即Catalan数
n得范围开long long不会溢出 所以用一个快一些的递推公式
$ h(n)=h(n−1)∗(4∗n−2)/(n+1) $
cat[0]=cat[1]=1;
for(int i=2;i<=n;++i)
cat[i]=cat[i-1]*(4*i-2)/(i+1);
方格问题
在n*n的格子中,只在下三角行走,每次横或竖走一格,有多少中走法?
其实向右走相当于进栈,向左走相当于出栈,本质就是n个数出栈次序的问题,所以答案就是卡特兰数。
二叉搜索树问题
**QUESTION ** 有n个结点,问总共能构成几种不同的二叉树
如果采用中序遍历的话,根结点第k个被访问到,则根结点的左子树有k-1个点、根结点的右指数有n-k个点。k的取值范围为1到n,公式1显然可推
**QUESTION ** 有n+1个叶子的满二叉树的个数?
向左记为+1,向右记为−1,按照向左优先的原则,从根节点开始遍历.例如第一个图记为+1,+1,+1,−1,−1,−1,于是由卡特兰数的含义可得满二叉树的个数为Cn
凸多边形的三角形划分问题
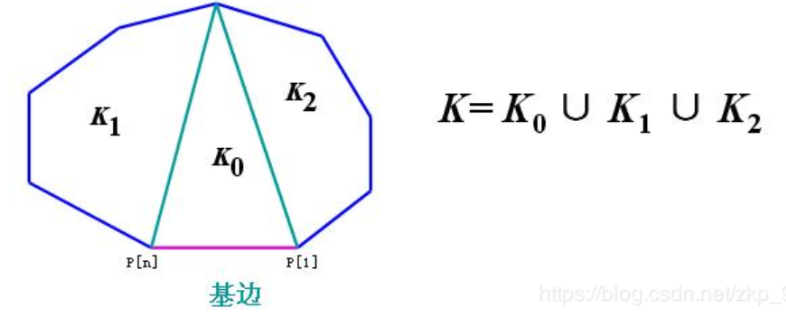
**QUESTION ** 一个凸的n边形,用直线连接他的两个顶点使之分成多个三角形,每条直线不能相交,问一共有多少种划分方案。
选择一个基边,显然这是多边形划分完之后某个三角形的一条边。图中我们假设基边是p1pn,我们就可以用p1、pn和另外一个点假设为pi做一个三角形,并将多边形分成三部分,除了中间的三角形之外,一边是i边形,另一边是n-i+1边形。i的取值范围是2到n-1。所以本题的解c(n)=c(2)c(n-1)+c(3)c(n-2)+…c(n-1)c(2)。令t(i)=c(i+2)。则t(i)=t(0)t(i-1)+t(1)t(i-2)…+t(i-1)t(0)