Weighted Quick Union

Weighted Quick Union即:

在Quick Union的基础上对结点加权(weighted),在parent[i]基础上增加一个size[i].

用来存储该结点(site)的所有子结点数目.(size[i] == number of sites in subtree rooted at i)

具体操作步骤:

仅仅在union() operation改变,在改变parent前,增加一个步骤:

比较两个结点的size,谁更轻谁就在下面,

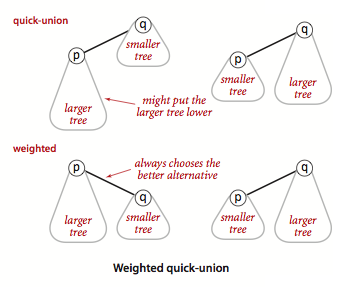
具体看代码:

class WeightedQuickUnion():
    __count = int()     #number of components
    __parent = list()   #__parent[i] parent of i
    __size = list()     #size[i] number of sites in subtree rooted at i
    #Each site is initially in its own component
    def __init__(self,N):
        self.__count = N
        for i in range(0,self.__count):
            self.__parent.append(i)
            self.__size.append(1)
    #Return the component identifier for the component containing site
    def find(self,p):
        self.validate(p)
        while (p != self.__parent[p]):
            p = self.__parent[p]
        return p
    def connected(self,p,q):
        return self.find(p) == self.find(q)
    #Merges the component containig site p with
    #the component containing site q
    def union(self,p,q):
        rootP=self.find(p)
        rootQ=self.find(q)
        if (rootP == rootQ):
            return
        if (self.__size[rootP] < self.__size[rootQ]):
            self.__parent[rootP] = rootQ
            self.__size[rootQ] += self.__size[rootP]
        else:
            self.__parent[rootQ] = rootP
            self.__size[rootP] += self.__size[rootQ]
        self.__count-=1
    def validate(self, p):
        n = len(self.__parent)
        if (p < 0 or p >= n):
            raise ValueError("index", p, "is not between 0 and", (n - 1))
    def traversal(self):
        for i in self.__parent:
            print(i,end=' ')
WQU = WeightedQuickUnion(8)
WQU.union(0,1)
WQU.union(2,1)
WQU.union(2,4)
WQU.union(3,7)
print(WQU.connected(0,4))
WQU.traversal()

实例同上一文Quick Find一样,

连接0-1-2-4 3-7,并调用connected()方法验证0-4是否连接

最后遍历

输出:

True
0 0 0 3 0 5 6 3 

根据输出可以反应出树形图:

　　　　　　0　　　　3　　5　　6

　 　　/　　|　　　　|

　　1　　　2　　4     7

程序中:union()方法里,把size的比较分为两种情况,小于以及大于+等于.

union(0,1)的时候0是p,1是q,他们的size都是1,所以会执行

            self.__parent[rootQ] = rootP
            self.__size[rootP] += self.__size[rootQ]

也就是q(1)会成为p(0)的子节点.

union(3,7)同理.

其它情况由于size不同,会按照程序写的那样,把轻的作重的子节点