【bzoj1951】: [Sdoi2010]古代猪文 数论-中国剩余定理-Lucas定理

【bzoj1951】: [Sdoi2010]古代猪文

因为999911659是个素数

欧拉定理得

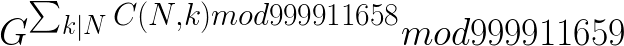
然后指数上中国剩余定理

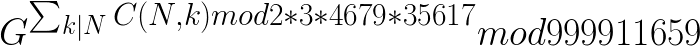
 然后分别lucas定理就好了

注意G==P的时候的特判

/* http://www.cnblogs.com/karl07/ */
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
#define ll long long

const ll P=999911659;
const ll p1[5] = {0, 2, 3, 4679, 35617};
const ll N=40000;
ll g,n,cnt=0;
ll fac[N+5],ifac[N+5];
ll p[N],ans[5];

ll Q_pow(ll a,ll b,ll p){
    ll ans=1;
    while (b){
        if (b&1) ans=ans*a%p;
        a=a*a%p;
        b=(b>>1);
    }
    return ans;
}

void FAC(ll p){
    ifac[0]=fac[0]=1;
    for (int i=1;i<=N;i++) fac[i]=fac[i-1]*i%p,ifac[i]=Q_pow(fac[i],p-2,p);
}

ll C(ll n,ll m,ll p){
    if (m>n) return 0;
    return fac[n]*ifac[m]%p*ifac[n-m]%p;
}

ll lucas(ll n,ll m,ll p){
    if (m==0) return 1;
    return lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;
}

void fj(ll x){
    for (int i=1;i*i<=x;i++){
        if (x%i==0){
            p[++cnt]=i;
            if (i*i!=x) p[++cnt]=n/i;
        }
    }
}

ll gcd(ll a,ll b){return b ? gcd(b,a%b) : a;}

void ex_gcd(ll a,ll b,ll &x,ll &y){
    if (b==0){x=1;y=0;return;}
    ex_gcd(b,a%b,y,x);
    y-=x*(a/b);
}


ll China(){
    ll a0=ans[1],p0=p1[1];
    for (int i=2;i<=4;i++){
        ll x,y,g=gcd(p0,p1[i]);
        ex_gcd(p0,p1[i],x,y);
        x=(x*(ans[i]-a0)%p1[i]+p1[i])%p1[i];
        a0=a0+x*p0;
        p0=p0/g*p1[i];
    }
    return a0;
}

void work(){
    for(int i=1;i<=4;i++){
        FAC(p1[i]);
        for (int j=1;j<=cnt;j++){
            ans[i]=(ans[i]+lucas(n,n/p[j],p1[i]))%p1[i];
        }
    }
    printf("%lld
",Q_pow(g,China(),P));
}

int main(){
    scanf("%lld%lld",&n,&g);
    if (g==P) {puts("0"); return 0;}
    fj(n);
    work();
    return 0;
}
　　

各种zz的错误。。调了一年

而且跑的巨慢无比。。