利用子集构造法实现NFA到DFA的转换

• 概述

NFA非有穷自动机，即当前状态识别某个转换条件后到达的后继状态不唯一，这种自动机不便机械实现，而DFA是确定有限状态的自动机，它的状态转换的条件是确定的，且状态数目往往少于NFA，所以DFA能够比较方便的机械实现且识别能力方面也和NFA相当。本次实验采用子集构造法来实现不带空弧的由NFA到DFA的转换。

 

子集构造法的算法如下：

设NFA为M=(K,Σ,f,S0,Z)，则构造相应的DFA  M′=(Q,Σ,f′,I0,F)
①取I0=S0；
②对于状态集Q中任一尚未标记的状态qi={Si1,Si2,…,Sim},Sik∈K，做：
 (1) 标记qi；
 (2) 对于每个a∈Σ，置
     T=f({Si1,Si2,…,Sim},a)
     qj=εCLOSURE(T)
 (3) 若qj不在Q中，则将qj作为一个未加标记的状态添加到Q中，且把状态转移f′(qi,a)=qj添加到M′。
③重复进行步骤②，直到Q中不再含有未标记的状态为止。对于由此构造的Q，我们把那些至少含有一个Z中的元素的qi作为M′的终态。

 

对于如图所示的NFA其在文件中保存的信息如下

 

转成DFA之后的形式为

 

重命名为

• 程序整体思路

首先将文件中所给的NFA输入读入程序，在读入过程中将其以图的邻接表的形式保存，其中将状态转移条件记为该边的权值，每种状态记为图的结点，该状态识别状态转移条件(权值)之后到达的状态为该结点的邻接点。

 

对于上面的例子，将其读入程序中后该图在程序中的逻辑存储结构（图的邻接表）如图所示，其中邻接点中第一个数字表示权值，第二个数字表示所连的结点。

将图读入程序中后，再使用子集构造算法来完成由NFA到DFA的转化。

 

对于每种状态，其数据结构定义为

typedef struct state
{
    set<int> Set;
    char name;
}state;

其中set里存放该状态识别某个条件后所能到达的状态集合的下标，name里存该状态重命名后的名字。

 

这些状态保存在状态数组States[max]中，状态数组States[max]数据结构定义为

state States[max];

子集构造法的过程就是不断向状态数组States[ ]中，添加识别某个条件后，新的未出现的状态的过程。

 

程序中函数说明

void creatph(algraph &g,FILE *fpr)：将文件内容读入程序，并将其转换为图的邻接表子函数。

int change(algraph g,char p)：将图中结点转化为对应下标子函数。

state move(state s,int n,algraph g)：求当前状态集合的转移集合，即求s状态识别字母n之后的状态集合。

int equalSet(state m,state n)：比较两个状态的set集合内容是否相等，不相等返回0，相等返回1。

void inStates(state &s)：判断当前状态是否在States数组中存在，若存在，进行改名；若不存在，改名后加入States数组。

void changeToD(algraph g,FILE *fpw)：由NFA转到DFA的主控程序子函数。

程序输入如下图所示

 

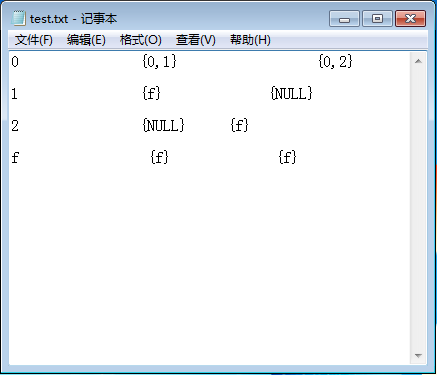
程序输出如下图所示

 

•  代码清单

#include<stdio.h>
#include<malloc.h>
#include <iostream>
#include <fstream>
#include <cstring>
#include<set>

using namespace std;

#define max 50//定义结点最大数量
typedef char vertype;//定义结点值域为字符类型
char buf[1024];//定义读文件内容时，程序缓冲数组
int num;//记录有穷字母表元素的个数
int length;//记录States数组的长度

typedef struct arcnode//图的边信息
{
    int adjvex;
    int weight;//边所对应的权值
    struct arcnode *next;
}arcnode;

typedef struct vnode//图的结点类型定义
{
    vertype data;
    arcnode *next;
}vnode,adjlist[max];

typedef struct//图的定义
{
    adjlist a;
    int vexnum,arcnum;
}algraph;

typedef struct state//状态的定义
{
    set<int> Set;
    char name;
}state;

state States[max];

int change(algraph g,char p)//将图中结点转化为对应下标
{
    int i;
    for(i=0;i<g.vexnum;i++)
    {
        if(p==g.a[i].data)
            return i;
    }
    return -1;
}

void creatph(algraph &g,FILE *fpr)
{
    int line = 0;
    while(!feof(fpr))
    {    
        fgets(buf,1024,fpr);
        if(strlen(buf)>1)//获取文件中图的结点个数
        {    
            int i = 0;
            while(buf[i]==' ')
            {
                i++;
            }
            
            g.a[line].data=buf[i];
            g.a[line].next=NULL;
            line++;
        }
    }
    g.vexnum=line;
    
    rewind(fpr);//将文件指针返回到开头位置
    line = 0;
        arcnode *s;

    while(!feof(fpr))//再次扫描文件将边的信息添上，构造图
    {    
        int weight=0;//边所对应的权值,每一行权值都从0开始
        fgets(buf,1024,fpr);
        if(strlen(buf)>1)
        {
            for(int i=0;i<strlen(buf)-1;i++)
            {
                if(buf[i]=='{')
                {    
                    weight++;    
                    if(num<weight)
                        num=weight;

                    i++;    
                    if(buf[i]=='N')
                            i=i+4;

                    while(buf[i]!='}')
                    {    
                        if(buf[i]!=',')
                        {
                            //cout<<buf[i];////////////////////////////////
                            int x = change(g,buf[i]);

                            s=(arcnode *)malloc(sizeof(arcnode));
                            s->adjvex=x;
                            s->weight=weight;
                            s->next=g.a[line].next;
                            g.a[line].next=s;
                            //cout<<line;////////////////////////////////
                        }
                        i++;
                    }
                }
            }
            line++;
        }    
    }

}

state move(state s,int n,algraph g)//求当前状态集合的转移集合，即求s状态识别字母n之后的状态集合
{
    state temp;
    arcnode *m;
    set<int>::iterator itr;//迭代器
    for(itr = s.Set.begin();itr!=s.Set.end();itr++)//遍历当前s状态中集合元素 
    {
        int i = *itr;
        m = g.a[i].next;
        while(m)
        {
            if(m->weight==n)
            {
                temp.Set.insert(m->adjvex);//cout<<m->adjvex<<" ";
            //    temp.name=s.name+1;//cout<<temp.name<<endl;
            }
            m=m->next;
        }
    }
    return temp;    
}

int equalSet(state m,state n)//比较两个状态的set集合内容是否相等
{
    int flag = 1;
    if(m.Set.size()!=n.Set.size())
    {
        flag = 0;
        return flag;
    }

    set<int>::iterator itrm;
    set<int>::iterator itrn;
    for(itrm = m.Set.begin(),itrn = n.Set.begin();itrm!=m.Set.end();itrm++,itrn++)
    {
        int m = *itrm;
        int n = *itrn;

        if(m!=n)
        {
            flag = 0;
            break;
        }
    }
    return flag;
}

void inStates(state &s)//判断当前状态是否在States数组中存在，若存在，进行改名；若不存在，改名后加入States数组
{
    int flag = 0;
    if(length==0)
    {
        States[0]=s;
        States[0].name='A';
        length++;
    }
    else
    {
        for(int i=0;i<length;i++)
        {
            //cout<<equalSet(States[i],s);
            if(equalSet(States[i],s)==1)//若存在，进行改名
            {
                s.name=States[i].name;
                flag = 1;
                break;
            }
        }

        if(flag == 0)//若不存在，改名后加入States数组
        {
            s.name=States[length-1].name+1;
            States[length]=s;
            length++;
        }
    }
}

void changeToD(algraph g,FILE *fpw)
{
    state s,temp;
    s.Set.insert(0);
    s.name='A';

    inStates(s);

    for(int i=0;i<length;i++)
    {    
        cout<<"{";
        fprintf(fpw,"{");

        set<int>::iterator itr;//迭代器
        for(itr = States[i].Set.begin();itr!=States[i].Set.end();itr++)//遍历当前s状态中集合元素 
        {
            int i = *itr;
            cout<<g.a[i].data<<",";
            fprintf(fpw,"%c,",g.a[i].data);
        }

        cout<<"}";
        fprintf(fpw,"}");

        cout<<States[i].name;
        fprintf(fpw,"%c",States[i].name);

        for(int j=1;j<=num;j++)
        {
            temp = move(States[i],j,g);
            inStates(temp);    
            //查看temp状态的set集合
            /*    
            set<int>::iterator itr;//迭代器
            for(itr = temp.Set.begin();itr!=temp.Set.end();itr++)//遍历当前s状态中集合元素 
            {
                int i = *itr;
                cout<<i<<" ";
            }*/    
            cout<<temp.name;
            fprintf(fpw,"%c",temp.name);    
        }
        cout<<endl;    
        fprintf(fpw,"
");
    }
}


int main()
{
    algraph g;

    FILE *fpr = fopen("F:\test.txt","r");
    FILE *fpw = fopen("F:\testOutput.txt","w");
    

/*    FILE *fpr = fopen("test.txt","r");
    FILE *fpw = fopen("output.txt","w");*/

    creatph(g,fpr);

    //create测试
    /*
    for(int i=0;i<g.vexnum;i++)
    {
        cout<<g.a[i].data<<endl;//////////////////

    }
    */

    changeToD(g,fpw);
    //move测试
    /*
    state s;
    s.Set.insert(0);
    s.Set.insert(2);
    s.Set.insert(3);
    s.mark=1;
    s.name='B';

    move(s,2,g);
    */
    return 0;
}