二项逻辑回归模型是如下的条件概率分布:
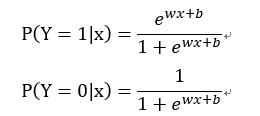
其中x∈是输入,y∈{0,1}是输出。
为了方便,将权值向量和输入向量进行扩充,此时w =  ,x =
,x = 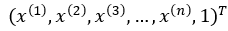 ,回归模型表示如下:
,回归模型表示如下:

参数w未知,采用统计学中的极大似然估计来由样本估计参数w。对于0-1分布x ~ B(1 , p),x的概率密度函数可以表示为:
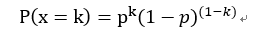
其中k = 0或1。
构造极大似然函数:
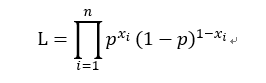
取对数得:

同理对于二项逻辑回归,我们令:

则其似然函数为:

其中yi取值为0或1。
取对数得:
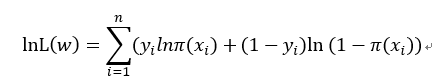
求上式的最大值等价于对上式取负号后的最小值问题,得:

问题就转换成了以对数似然函数为目标函数的最优化问题,对于该最优化问题常使用梯度下降法或拟牛顿法。
通常把逻辑回归问题的代价函数定义成以上形式,对数似然函数在y=0或是y=1其图像如下如所示
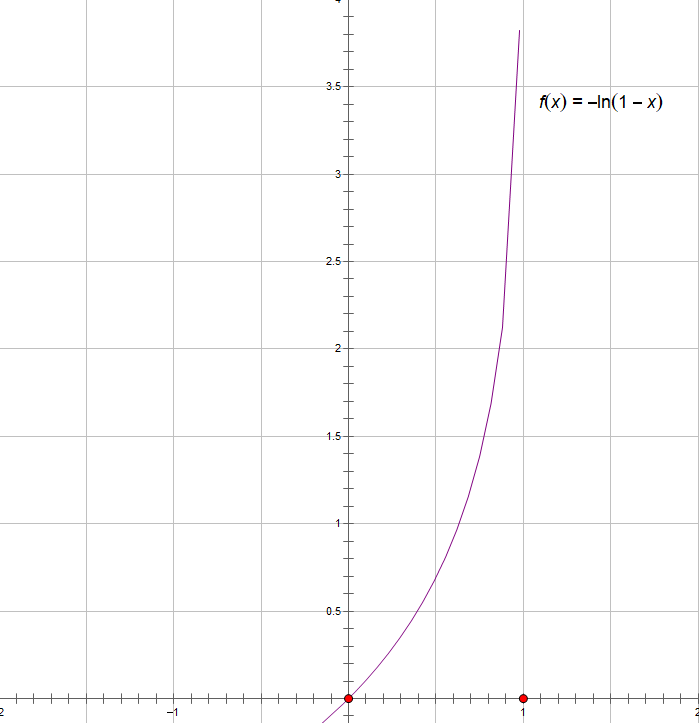

这样可以保证代价函数是一个凸函数,使用梯度下降算法时,可以得到全局最优解。