二进制是计算技术中广泛采用的一种数制。 二进制数据是用0和1两个数码来表示的数。
二进制的表现形式
计算机中的符号数有三种表示方法,即原码、反码和补码。三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,而数值位,三种表示方法各不相同。
正数在计算机中以原码的形式存在,而负数以补码的形式存在。
| 原码 | 反码 | 补码 | |
|---|---|---|---|
| 正数(5) | 0000 0101 | 0000 0101 | 0000 0101 |
| 负数(-5) | 1000 0101 | 1111 1010 | 1111 1011 |
| 小数(5.125) | 0101.001 | 0101.001 | 0101.001 |
-
原码:符号位+数据位,正数符号位位0,负数符号位为1;
-
正数的原码和补码相同;负数的反码等于其原码符号位不变,其余各位取反;
-
正数的原码和补码相同;负数的补码等于其原码取反加一;负数的原码等于其补码符号位不变,减一取反。
原码
负数:-5
原码:1000 0101
反码
负数:-5
原码:1000 0101
反码:1111 1010
补码
负数:-5
原码:1000 0101(符号位+数据位)
反码:1111 1010 (符号位不变,各位取反)
补码:1111 1011 (反码+1)
二进制的转换
二进制转十进制
正整数
二进制:0000 0101
十进制:1 + 0*2 + 1*2*2 = 5
负整数
二进制:1111 1011(负数以补码形式存在)
十进制:
- 二进制反码:1111 1010
- 二进制原码:1000 0101
- 二进制原码转十进制:- 1+0*2+1*2*2 = -5
小数
二进制:0101.001
十进制:
- 整数部分:0101 = 5
- 小数部分:1000 = 0*1/2 + 0*1/4+ 0*1/8=0.125
- 合并:5+0.125 = 5.125

十进制转二级制
正整数
十进制:5
二进制:0000 0101
负整数
十进制:-5
二进制:
- -5的原码:1000 0101
- -5的反码:1111 1010
- -5的补码:1111 1011
小数
十进制:5.125
二进制:0101.001

二进制的运算
运算符号
运算逻辑
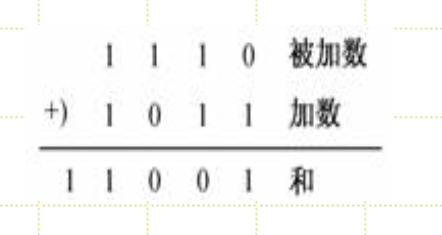
(1)二进制数的加法
根据“逢二进一”规则,二进制数加法的法则为:
0+0=0
0+1=1+0=1
1+1=0 (进位为1)
1+1+1=1 (进位为1)
例如:1110和1011相加过程如下:
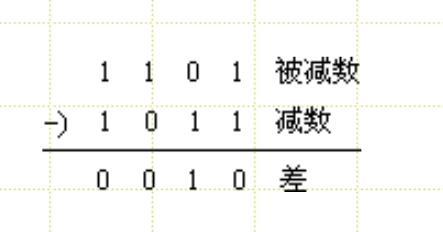
(2)二进制数的减法
根据“借一有二”的规则,二进制数减法的法则为:
0-0=0
1-1=0
1-0=1
0-1=1 (借位为1)
例如:1101减去1011的过程如下[1]:
(3)二进制数的乘法
二进制数乘法过程可仿照十进制数乘法进行。但由于二进制数只有0或1两种可能的乘数位,导致二进制乘法更为简单。二进制数乘法的法则为:
0×0=0
0×1=1×0=0
1×1=1
例如:1001和1010相乘的过程如下:
由低位到高位,用乘数的每一位去乘被乘数,若乘数的某一位为1,则该次部分积为被乘数;若乘数的某一位为0,则该次部分积为0。某次部分积的最低位必须和本位乘数对齐,所有部分积相加的结果则为相乘得到的乘积。
(4)二进制数的除法
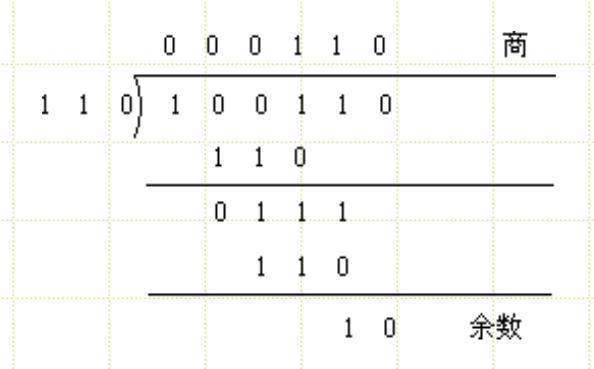
二进制数除法与十进制数除法很类似。可先从被除数的最高位开始,将被除数(或中间余数)与除数相比较,若被除数(或中间余数)大于除数,则用被除数(或中间余数)减去除数,商为1,并得相减之后的中间余数,否则商为0。再将被除数的下一位移下补充到中间余数的末位,重复以上过程,就可得到所要求的各位商数和最终的余数。
例如:100110÷110的过程如下:
所以,100110÷110=110余10。
说明:乘除法分原码乘法和补码乘法。
(5)逻辑“或”运算
又称为逻辑加,可用符号“+”或“∨”来表示。逻辑“或”运算的规则如下:
0+0=0或0∨0=0
0+1=1或0∨1=1
1+0=1或1∨0=1
1+1=1或1∨1=1
可见,两个相“或”的逻辑变量中,只要有一个为1,“或”运算的结果就为1。仅当两个变量都为0时,或运算的结果才为0。计算时,要特别注意和算术运算的加法加以区别。
(6)逻辑“与”运算
又称为逻辑乘,常用符号“×”或“· ”或“∧”表示。“与”运算遵循如下运算规则:
0×1=0或0·1=0或0∧1=0
1×0=0或1·0=0或1∧0=0
1×1=1或1·1=1或1∧1=1
可见,两个相“与”的逻辑变量中,只要有一个为0,“与”运算的结果就为0。仅当两个变量都为1时,“与”运算的结果才为1。
(7)逻辑“非”运算
又称为逻辑否定,实际上就是将原逻辑变量的状态求反,其运算规则如下:
可见,在变量的上方加一横线表示“非”。逻辑变量为0时,“非”运算的结果为1。逻辑变量为1时,“非”运算的结果为0。
(8)逻辑“异或”运算
“异或”运算,常用符号“”或“”来表示,其运算规则为:
00=0 或 00=0
01=1 或 01=1
10=1 或 10=1
11=0 或 11=0
可见:两个相“异或”的逻辑运算变量取值相同时,“异或”的结果为0。取值相异时,“异或”的结果为1