一、特征选择基本问题
我们将属性称为“特征”(feature),对当前学习任务有用的属性称为“相关特征”(relevant feature)、没什么用的属性称为“无关特征”(irrelevant feature)。
从给定的特征集合中选择出相关特征子集的过程,称为“特征选择”(feature select)。
1-1、为什么要进行特征选择
第一,为了处理维数灾难(减轻维数灾难的另一种方法是降维);
第二,去除不相关特征往往会降低学习任务的难度。
对于同样的数据集,若学习任务不同,则相关特征很有可能不同,因此,特征选择中所谓的“无关特征”是指与当前学习任务无关。
冗余特征(redundant feature):该类特征所包含的信息能从其他特征中推演出来。例如,考虑立方体对象,若已有特征“底面长”、“底面宽”,则“底面积”是冗余特征。
冗余特征在很多时候不起作用,去除它们会减轻学习过程的负担。但有时冗余特征会降低学习任务难度,例如学习目标是估算立方体的体积,则“底面积”这个冗余特征的存在
使得体积的估算更容易;更确切地说,若某个冗余特征恰好对应了完成学习任务所需的“中间概念”,则该冗余特征是有益的。
1-2、子集搜索与评价
子集搜索(subset search):给定特征集合{a1,a2,...,ad}。
前向搜索:将每个特征看做一个候选子集,对这d个候选单特征自己进行评价。
从单特征子集开始逐渐增加特征,每次增加一个特征,使得每次增加特征后的子集优于之前的子集,直到最优的候选子集不如前一轮的子集时,停止增加子集。
后向搜索:从完整的特征集开始,每次尝试去掉一个无关特征。
子集评价(subset evaluation):
判断两个不同子集哪个较优可以通过信息增益(两次信息熵的差值)来判断。信息增益越大,意味着特征子集包含的有助于分类的信息越多。
将前向搜索与信息熵的子集评价结合,即与决策树算法十分相似。
事实上,决策树(基于树的分类器)可以用于特征选择,树结点的划分属性所组成的集合就是选择出的特征子集。
二、特征选择的主要方法
2-1、过滤式(Filter)
过滤式方法先对数据集进行特征选择,然后再训练学习器,特征选择过程与后续学习器无关。
其主要思想是为每一个特征计算一个权重,这样的权重就代表着该维特征的重要性,然后依据权重排序。
主要的方法有:Relief(Relevant Features)。
2-2、包裹式(Wrapper)
与过滤式特征选择不考虑后续学习器不同,包裹式特征选择直接把最终将要使用的学习器的性能作为特征子集的评价准则。
从最终学习器性能来看,包裹式特征选择比过滤式特征选择更好,但是计算开销也大的多。
其主要思想是将子集的选择看作是一个搜索寻优问题,生成不同的组合,对组合进行评价,再与其他的组合进行比较。
这样就将子集的选择看作一个优化问题,这里有很多的优化算法可以解决,尤其是一些启发式的优化算法。
主要方法有:LVW(Las Vegas Wrapper)。
2-3、嵌入式(Embedding)
在过滤式和包裹式特征选择方法中,特征选择过程与学习器训练过程有明显区别;
而嵌入式特征选择是将特征选择过程与学习器训练过程融为一体,两者在同一个优化过程中完成,即在学习器训练过程中自动地进行了特征选择。
其主要思想是:在模型既定的情况下学习出对提高模型准确性最好的属性。即在确定模型的过程中,挑选出那些对模型的训练有重要意义的属性。
主要方法有:岭回归(ridge regression),岭回归就是在基本线性回归的过程中加入了L2正则项。
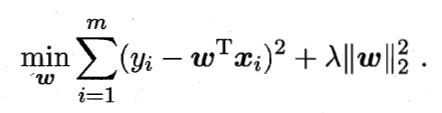
将L2正则项换成L1正则项时,称为LASSO。

L1范数(模)和L2范数(模)正则化都有助于降低过拟合风险,但前者还会带来“稀疏解”,即它求得的w会有更少的非零分量。
直观的例子如下:假定数据集仅有两个属性,因此求解得到的w也只有两个分量,即w1,w2,我们将其作为两个坐标轴,然后绘制上面两个式子的“等值线”,
即在(w1,w2)空间中平方误差项取值相同的点的连线,再分别绘制L1范数和L2范数的等值线。
从图可知,使用L1范数时平方误差项等值线与正则化等值线的交点常出现在坐标轴上,即w1或w2为0;而采用L2范数时,两者的交点常出现在某个象限中,即w1和w2均非0.
因此,L1范数比L2范数更易于得到系数解。

参考文献
[1]. 周志华. 机器学习[M]. Qing hua da xue chu ban she, 2016.
[2]. 机器学习之特征选择
[3].几种常用的特征选择方法