决策树算法

信息熵

在之前的博文里，推到了KL散度、熵和极大似然的关系，理解了这个其实信息熵也很好理解。

对于随机变量\(X\) 有：

\[P(X=x_i) = p_i \]

因此\(X\) 这个随机分布的熵就是：

\[H(X) = -\sum_{i=1}^n p_i \log p_i \]

但我们谈变量的熵的时候，实际上谈的是分布。熵代表的物理意义就是我们需要用多少bit来表达这个分布 。

很显然，当分布越复杂，随机变量\(X\)分布的熵也就越大。可以说熵代表了随机变量的不确定性。

条件熵

条件熵\(H(Y|X)\) 表示随机变量\(Y\)在随机变量\(X\)确定的情况下的熵。

\[H(Y|X) = \sum_{i=1}^n p_i H(Y|X=x_i) \]

这里的\(x_i\)就是分类的决定特征条件。比如西瓜颜色有绿和浅绿，那么这个条件熵就是按这种特征划分后得到的新的样本集，再计算熵。

注意，这里的熵中的概率分布，是由极大似然得到的经验概率，也就是说这里的熵实际上是经验熵，条件熵也是经验条件熵。

信息增益

\(g(D, A) = H(D) - H(D|A)\)

一般来说，熵 \(H(Y)\) 与条件熵\(H(Y|X)\) 之差称为互信息。

决策树做的就是最大化信息增益。

信息增益算法

input: 训练数据集D 和特征 A

output: 特征对训练数据集的信息增益。

1. 计算数据集D的经验熵\(H(D)\)

\[H(D)=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log _{2} \frac{\left|C_{k}\right|}{|D|} \]

2. 计算按照特征A进行切分的条件经验熵\(H(D|A)\)

\[H(D \mid A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right)=-\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} \sum_{k=1}^{K} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \log _{2} \frac{\left|D_{i k}\right|}{\left|D_{i}\right|} \]

3. 计算信息增益
   \[g(D, A)=H(D)-H(D \mid A) \]

通过计算得到每个特征对训练集的划分的信息增益，挑选出能使信息增益最大的特征进行切分。

信息增益比

这个没啥好说的，就是变成了比值。

\[g_{R}(D, A)=\frac{g(D, A)}{H_{A}(D)} \]

决策树的生成算法

ID3算法

就是是特征增益最大化这一思想反复进行划分。注意，叶子结点可以是pure节点，也可以是信息熵低于阈值的节点。

C4.5算法

这玩意就是用信息增益比来划分的，换汤不换药。

决策树剪枝

\[C_{\alpha}(T)=\sum_{t=1}^{|T|} N_{t} H_{t}(T)+\alpha|T| \]

\[H_{t}(T)=-\sum_{k} \frac{N_{t k}}{N_{t}} \log \frac{N_{t k}}{N_{t}} \]

\[C(T)=\sum_{t=1}^{|T|} N_{t} H_{t}(T)=-\sum_{t=1}^{|T|} \sum_{k=1}^{K} N_{t k} \log \frac{N_{t k}}{N_{t}} \]

\[C_{\alpha}(T)=C(T)+\alpha|T| \]

说白了，就是加了一个\(|T|\) ，也就是叶节点的个数，这个有点像岭回归里的正则项，作用应该就是一样的，就是降低模型的复杂度。

剪枝算法

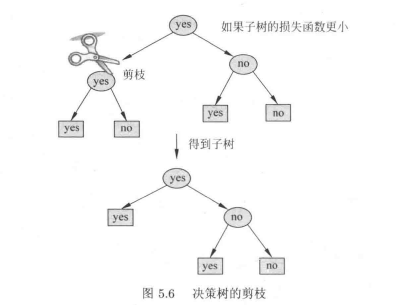
因为剪枝后，叶节点的个数下降，所以剪枝后，可能\(C_{\alpha}(T_{后}) \leq C_{\alpha}(T_{前})\)

CART算法

回归树生成

就是一个优化问题，不断去试划分点和划分变量。

\[\min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right] \]

这里用的还是最小二乘法实现，所以这个树就是二叉树。

分类树实现

因为CART树是二叉树，所以对于离散变量的划分就是是和否的关系。

这里用的是基尼系数作为划分的依据，而不是信息增益。

可以看到基尼指数定义就很简单：\(1-\sum_{k=1}^K p_k^2\)

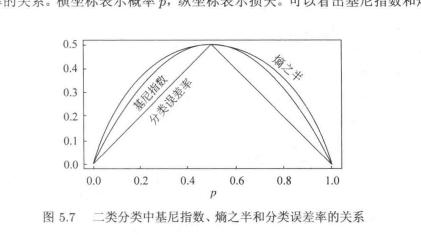
这里这张图可以看到，分布越随机，即p=0.5，基尼系数也就达到了越大。

对于分类树，很简单就是去计算每个特征的基尼指数，挑选出基尼指数最小的那个特征用做划分特征。

就是把信息增益换成了基尼指数，换汤不换药。

CART剪枝算法

CART的剪枝会剪出多个子树的，所以需要进一步去验证，找到最佳子树。