权重衰减
使用均方范数作为硬性限制

但我们最小化 loss 的时候,需要限制权重 w 的大小,越小的( heta) 意味着更强的正则项。
但实际上,我们不会这么做的,我们只是在做损失函数时候,加入了 (parallel w parallel ^2) ,就像下面做的那样。
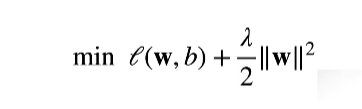
其中(lambda) = 0时候,就没有作用,而(lambda ightarrow infty) ,w就会趋于0。
这个(lambda) 是一个超参数,需要自己定义。
形象的显示:
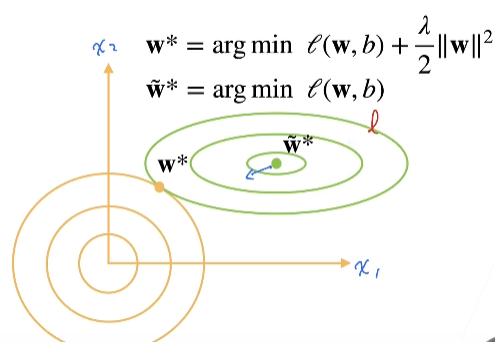
加入了 权重衰减后,w 会被拉到 (w^*)
参数更新:

Dropout
dropout和正则化的作用差不多,也是降低模型的过拟合性。

dropout 相当于在层之间加入噪音。但是加入噪音也不要改变其期望。

手写一个二层感知机代码:
import torch
import torch.nn as nn
import torch.nn.functional as F
class MLP(nn.Module):
def __init__(self, indim, hiddim, outdim, dropout):
super(MLP, self).__init__()
self.Lay1 = nn.Linear(indim, hiddim)
self.Lay2 = nn.Linear(hiddim, outdim)
self.dropout = dropout
def forward(self, x):
x = F.ReLU(self.Lay1(x))
x = F.dropout(x, self.dropout, training = self.training)
return self.Lay2(x)
net = MLP(indim, hiddim, outdim, dropout)
需要注意的是,当我需要训练时候,dropout才会发挥作用,而我预测时应该关掉dropout, dropout本质是作用在权重参数上的正则项。
net.train()# 开启训练
train(net)
net.eval()# 关掉训练
test(net)

注意dropout一般用在MLP上,CNN很少用,而且它只作用在隐藏层上。
数值稳定性
如果神经网络很深的话,就会有一系列问题,包括梯度爆炸和梯度消失。
梯度爆炸

可以看到,梯度反向传播会计算很多次矩阵乘法。

关于下面这个公式的推导:
它实际上来源于:
但是因为引入了激活函数,所以需要做一个对角矩阵。
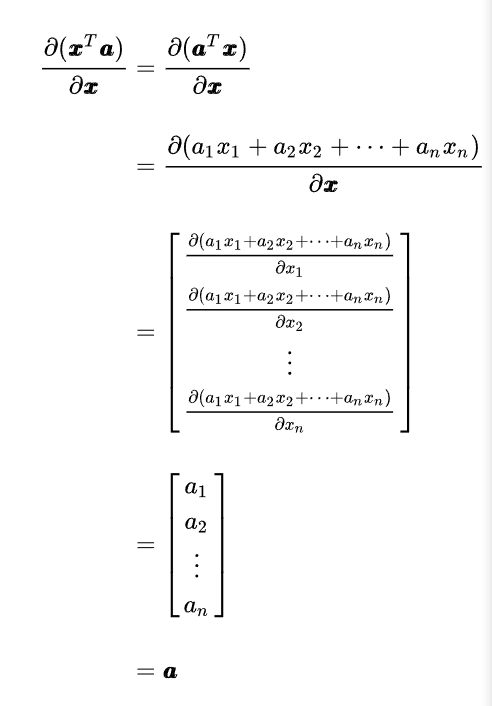
可以看到就是多了一个激活函数,基本求导思路没有变。
重新来看梯度爆炸:

梯度爆炸产生的原因就是我们累乘了多个W。
- 学习率太大了,可能导致大参数,大梯度
- 学习率低,训练也没有进展。
- 这就需要在学习中动态调整学习率。
梯度消失
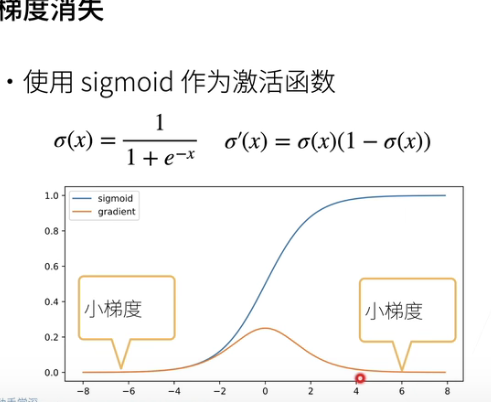
可以看到当数值大的时候,SIGMOD函数对应的导数就很小,还记得先前的那个公式吗?
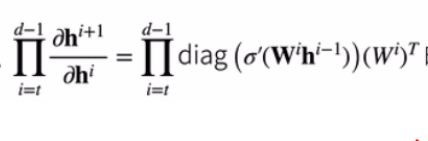
可以看到(prod_{i=t}^{d-1}diag(sigmaprime(W^ih^(i-1)))),这玩意就会快速接近0,最终导致梯度消失。
可以看到,梯度爆炸和梯度消失,实际上都和激活函数有点关系,但产生的原因还是不一样的。
当数值太大或者太小都会导致数值问题。
模型初始化和激活函数
因为数值太大或者太小都会导致数值问题,所有需要让梯度值在合理的范围内。

梯度归一化
基本思路:
-
将每层的输出和梯度都看做随机变量。
-
让每一层的均值和方差都保持一致。

权重初始化
权重初始化和随机数种子实际上也可以视为是一种超参数。

因为训练刚开始越容易数值不稳定,所以需要找到一个好的权重初始化方式,刚才提到了我们要让梯度每一层的方差和期望都一致。
以 MLP 为例:
正向输出

这个思路有点像数学归纳法,(E(h^{t-1}) =0 ightarrow E(h^t) = 0),再来看方差,证明思路还是一样。

反向梯度
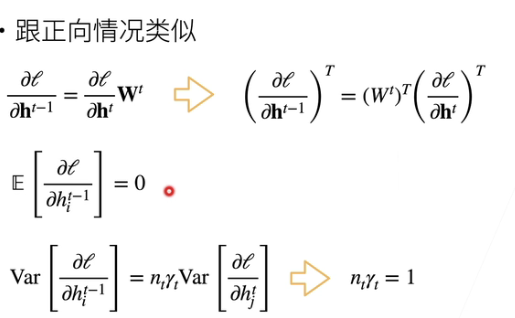
Xavier初始化

Xavier之前在GCN里见到过,当时还奇怪为什么用这种Xavier初始化方式,原来理由是为了数值稳定性。
各种激活函数
线性激活函数
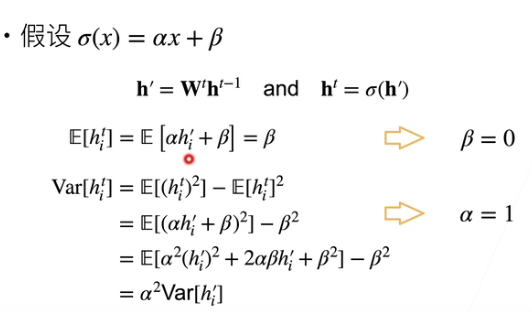
这意味着激活函数需要是(f(x) = x)
其他常用激活函数

在零点是,可以认为是(f(x) = x),对sigmoid需要进行调整。
总结
权重衰减和dropout实现的都是正则化的效果,使用它们的目的就是降低模型的复杂性,防止过拟合。
在数值稳定性一节里,讲到了为什么会出现梯度爆炸和梯度消失两个问题,维持数值稳定性的两个很重要的点——初始化和激活函数。