MATLAB常微分方程数值解——欧拉法、改进的欧拉法与四阶龙格库塔方法

MATLAB常微分方程数值解

作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/

1.一阶常微分方程初值问题

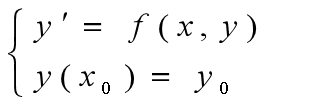
2.欧拉法

 

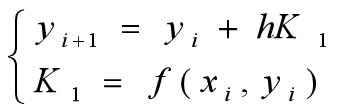
3.改进的欧拉法

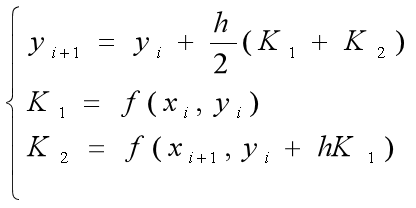
4.四阶龙格库塔方法

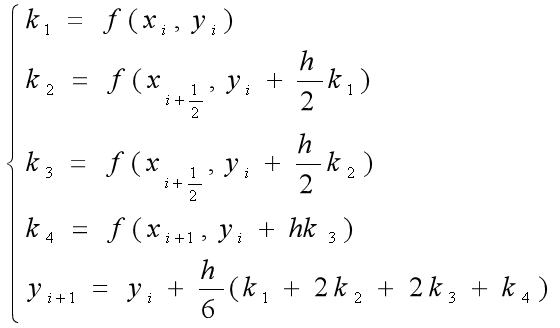
5.例题

用欧拉法，改进的欧拉法及4阶经典Runge-Kutta方法在不同步长下计算初值问题。步长分别为0.2,0.4,1.0.

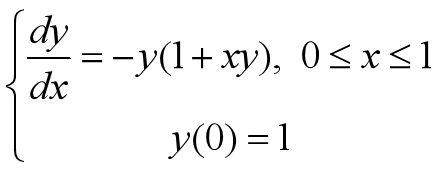
matlab程序：

function z=f(x,y)
z=-y*(1+x*y);

function R_K(h)
%欧拉法
y=1;
fprintf('欧拉法：x=%f, y=%f
',0,1);
for i=1:1/h
    x=(i-1)*h;
    K=f(x,y);
    y=y+h*K;
    fprintf('欧拉法：x=%f, y=%f
',x+h,y);
end
fprintf('
');
%改进的欧拉法
y=1;
fprintf('改进的欧拉法：x=%f, y=%f
',0,1);
for i=1:1/h
    x=(i-1)*h;
    K1=f(x,y);
    K2=f(x+h,y+h*K1);
    y=y+(h/2)*(K1+K2);
    fprintf('改进的欧拉法：x=%f, y=%f
',x+h,y);
end
fprintf('
');
 %龙格库塔方法
 y=1;
fprintf('龙格库塔法：x=%f, y=%f
',0,1);
for i=1:1/h
    x=(i-1)*h;
    K1=f(x,y);
    K2=f(x+h/2,y+(h/2)*K1);
    K3=f(x+h/2,y+(h/2)*K2);
    K4=f(x+h,y+h*K3);
    y=y+(h/6)*(K1+2*K2+2*K3+K4);
    fprintf('龙格库塔法：x=%f, y=%f
',x+h,y);
end

结果：

>> R_K(0.2)
欧拉法：x=0.000000, y=1.000000
欧拉法：x=0.200000, y=0.800000
欧拉法：x=0.400000, y=0.614400
欧拉法：x=0.600000, y=0.461321
欧拉法：x=0.800000, y=0.343519
欧拉法：x=1.000000, y=0.255934

改进的欧拉法：x=0.000000, y=1.000000
改进的欧拉法：x=0.200000, y=0.807200
改进的欧拉法：x=0.400000, y=0.636118
改进的欧拉法：x=0.600000, y=0.495044
改进的欧拉法：x=0.800000, y=0.383419
改进的欧拉法：x=1.000000, y=0.296974

龙格库塔法：x=0.000000, y=1.000000
龙格库塔法：x=0.200000, y=0.804636
龙格库塔法：x=0.400000, y=0.631465
龙格库塔法：x=0.600000, y=0.489198
龙格库塔法：x=0.800000, y=0.377225
龙格库塔法：x=1.000000, y=0.291009
>> R_K(0.4)
欧拉法：x=0.000000, y=1.000000
欧拉法：x=0.400000, y=0.600000
欧拉法：x=0.800000, y=0.302400

改进的欧拉法：x=0.000000, y=1.000000
改进的欧拉法：x=0.400000, y=0.651200
改进的欧拉法：x=0.800000, y=0.405782

龙格库塔法：x=0.000000, y=1.000000
龙格库塔法：x=0.400000, y=0.631625
龙格库塔法：x=0.800000, y=0.377556
>> R_K(1)
欧拉法：x=0.000000, y=1.000000
欧拉法：x=1.000000, y=0.000000

改进的欧拉法：x=0.000000, y=1.000000
改进的欧拉法：x=1.000000, y=0.500000

龙格库塔法：x=0.000000, y=1.000000
龙格库塔法：x=1.000000, y=0.303395

注意：在步长h为0.4时，要将for i=1:1/h改为for i=1:0.8/h。