P3515 [POI2011]Lightning Conductor（决策单调性分治）

P3515 [POI2011]Lightning Conductor

式子可转化为：$p>=a_j-a_i+sqrt(i-j) (j<i)$

$j>i$的情况，把上式翻转即可得到

下面给一张图证明这是满足决策单调性的

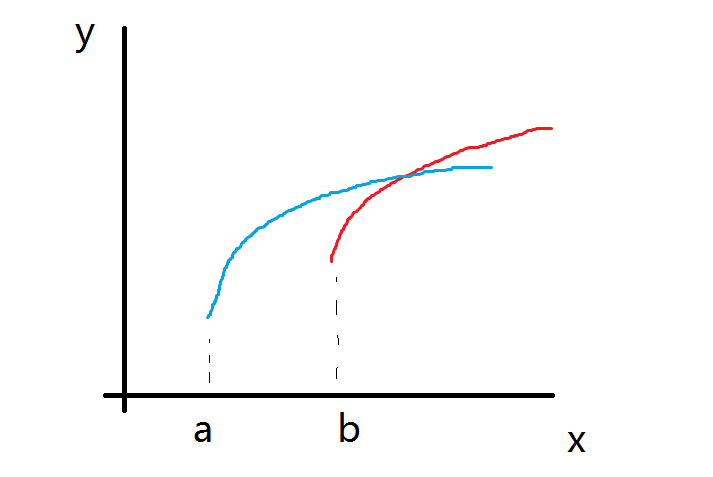
把$a_j+sqrt(i-j)$表示在坐标系上

显然$sqrt(i-j)$的增长速度趋缓

曲线$a$被曲线$b$超过后是无法翻身的

对两个方向进行决策单调性分治，取$max$即可

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int read(){
    char c=getchar(); int x=0,f=1;
    while(c<'0'||c>'9') f=f&&(c!='-'),c=getchar();
    while('0'<=c&&c<='9') x=x*10+c-48,c=getchar();
    return f?x:-x;
}
#define N 500005
int n,a[N]; double p1[N],p2[N],w;
void solve1(int l,int r,int dl,int dr){
    int m=(l+r)/2,dm=dl;
    for(int i=dl;i<=m&&i<=dr;++i)
        if(p1[m]<(w=a[i]-a[m]+sqrt(m-i)))
            p1[m]=w,dm=i;
    if(l<m) solve1(l,m-1,dl,dm);
    if(m<r) solve1(m+1,r,dm,dr);
}
void solve2(int l,int r,int dl,int dr){
    int m=(l+r)/2,dm=dr;
    for(int i=dr;i>=m&&i>=dl;--i)
        if(p2[m]<(w=a[i]-a[m]+sqrt(i-m)))
            p2[m]=w,dm=i;
    if(l<m) solve2(l,m-1,dl,dm);
    if(m<r) solve2(m+1,r,dm,dr);
}
int main(){
    n=read();
    for(int i=1;i<=n;++i) a[i]=read();
    solve1(1,n,1,n);
    solve2(1,n,1,n);
    for(int i=1;i<=n;++i)
        printf("%d
",(int)ceil(max(p1[i],p2[i])));
}