设前缀和为$s[i]$
那么显然可以得出方程
$f[i]=f[j]+(s[i]-s[j]+i-j-L-1)^{2}$
换下顺序
$f[i]=f[j]+(s[i]+i-(s[j]+j+L+1))^{2}$
为了处理方便,我们套路地设
$a[i]=s[i]+i$
$b[i]=s[i]+i+L+1$
于是得出
$f[i]=f[j]+(a[i]-b[j])^{2}$
拆开:$f[i]=f[j]+a[i]^{2}-2*a[i]*b[j]+b[j]^{2}$
移项:$f[j]+b[j]^{2}=2*a[i]*b[j]+f[i]-a[i]^2$
于是我们就把不变量和变量分开了($i$固定)
仔细观察
$f[j]+b[j]^{2}=2*a[i]*b[j]+f[i]-a[i]^2$
$y=k*x+b$
一次函数!
$y=f[j]+b[j]^{2}$
$k=2*a[i]$($i$递增时,显然它是单调递增的)
$x=b[j]$
$b=f[i]-a[i]^{2}$
如果我们要让$f[i]$最小,就是让$b$最小
而对于每个$i$,$k$是不变的
那么问题就转化成:找到一个最优的$(x,y)$使$b$最小
考虑到$k$是单调递增的
于是我们就可以快乐地用单调队列维护下凸包辣
while(L<R&&K(h[L],h[L+1])<=2*a(i)) ++L;//显然h[L]不比h[L+1]优,可以删去 f[i]=f[h[L]]+(a(i)-b(h[L]))*(a(i)-b(h[L]));//计算出最优的f[i] while(L<R&&K(h[R-1],h[R])>K(h[R],i)) --R;//加入点(x[i],y[i])后,h[R]在凸包内部,可以删去① h[++R]=i;//入队
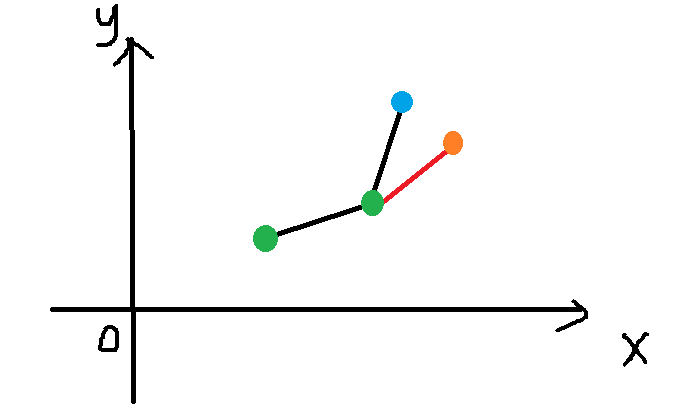
①:显然在加入橙点后,蓝点在凸包内部,可以被删除
#include<iostream> #include<cstdio> #include<cstring> using namespace std; typedef double db; #define N 50005 db f[N],s[N]; int n,l,L,R,h[N]; inline db a(int x){return s[x]+x;} inline db b(int x){return s[x]+x+l+1;} inline db X(int x){return b(x);} inline db Y(int x){return f[x]+b(x)*b(x);} inline db K(int x,int y){return (Y(x)-Y(y))/(X(x)-X(y));} int main(){ scanf("%d%d",&n,&l); for(int i=1;i<=n;++i) scanf("%lf",&s[i]),s[i]+=s[i-1]; L=R=1; for(int i=1;i<=n;++i){ while(L<R&&K(h[L],h[L+1])<=2*a(i)) ++L; f[i]=f[h[L]]+(a(i)-b(h[L]))*(a(i)-b(h[L])); while(L<R&&K(h[R-1],h[R])>K(h[R],i)) --R; h[++R]=i; }printf("%.0lf",f[n]); return 0; }