true beginning
高级程序设计语言的语法描述
文法:描述语言的语法结构的形式规则
比如在自然语言中
<句子> → <主语><谓语><直接宾语><间接宾语>
<主语> → <代词>
<谓语> → <动词>
<间接宾语> → <代词>
<直接宾语> → <冠词> <名词>
这样就定义了一个句子的组成形式
语法描述的基本概念
字母表:一个有穷字符集,记为Σ
字母表中的每个元素称为字符
Σ上的字(字符串):由Σ中的字符构成的一个有穷序列
不包含任何字符的序列称为空字,记为ε
Σ*表示Σ上所有字的全体(Σ上所有字符所能产生的字),包含空字ε
例:设Σ={ a,b },则
Σ* = { ε,a,b,aa,ab,bb,ba,aaa,…}
若U、V为Σ*的两个子集,则U和V的连接(积)定义为
UV = { αβ | α∈U & β∈V },顺序不可颠倒
例:设U = { a,aa }、V = { b,bb }
则UV = { ab,abb,aab,aabb }
V自身的n次积记为Vn
V0 = { ε }
V*是V的闭包:V*=V0∪V1∪V2∪V3∪…
V+是V的正规闭包:V+ = VV*
例:设U={ a,aa }
U* = { ε,a,aa,aaa,……}
U+ = { a,aa,aaa,aaaa,……}
可以看出正规闭包是不包含 ε 的闭包
上下文无关文法
高级程序设计语言使用上下文无关文法进行描述
至于文法的分类,请往后看
上下文无关文法G是一个四元组
G =(VT,VN,S,P)其中
VT:终结符(Terminal)集合(非空)
终结符:不可以再进行翻译的原子单位
VN:非终结符(Nonterminal)集合(非空),且 VT ∩ VN=∅
(一个非终结符往往是一个类/集合,比如算术表达式,代表一定算术表达式组成的类;
也可以说,一个非终结符表示一定符号串的集合)
S:文法的开始符号,(一个句子,从S开始翻译)S∈VN
P:产生式集合(有限),每个产生式形式为P→α,其中P∈VN,α∈(VT∪VN)*
开始符号S必须至少在某个产生式的左部出现一次,否则文法没有意义
例:定义只含+,*的算术表达式的文法 G = < { i,+,*,(,) },{E},E,P>,其中,P 由下列产生式组成:
E → i
E → E + E
E → E * E
E → (E)
通常
P → α1
P → α2
……
P → αn
简写为 P →α1|α2|…|αn
其中,| 读作 或,αi称为P的一个候选式
文法G简写为 G(E) : E → i | E+E | E*E | (E)
上面这种语法的描述形式称为巴克斯范式
巴克斯范式(BNF)是一种严谨描述文法的表达形式
由文法到语言
- 直接推出:当 A → γ 是一个产生式时,称αAβ直接推出αγβ,即 αAβ ⇒ αγβ,且 α,β ∈ ( VT ∪ VN )*
- 若α1 ⇒ α2 ⇒ … ⇒ αn,则我们称这个序列是 从α1到αn的一个推导。
若存在一个从α1到αn的推导,则称α1可以推导出αn

句型、句子和语言的概念

α 若可由 S 推导出,则称 α 是一个句型
仅含终结符号的句型是一个句子
文法G产生的句子的全体是一个语言
例:
请证明(i*i+i)是文法
G(E):E →i| E+E | E*E | (E)
的一个句子
证明: E ⇒ (E) ⇒ (E+E) ⇒ (E*E+E) ⇒ (i*E+E) ⇒ (i*i+E) ⇒ (i*i+i)
(i*i+i)是文法G的句子 E,(E),(E*E+E),…,(i*i+i)均是句型。
推导与语法树
从一个句型到另一个句型的推导往往不唯一
E + E ⇒ i + E ⇒ i + I
E + E ⇒ E + i ⇒ i + i
最左推导:任何一步 α ⇒ β 都是对 α 中的最左非终结符进行替换
最右推导:任何一步 α ⇒ β 都是对 α 中的最右非终结符进行替换
语法树:用一张图表示一个句型的推导,称为语法树
一棵语法树可以是不同推导过程的共性抽象
比如下面这棵树
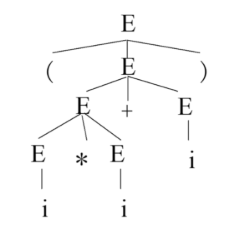
既可以表示最左推导,也可以表示最右推导的过程
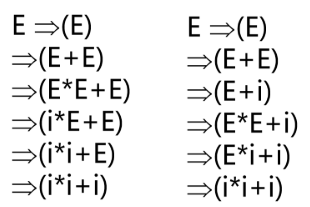
只是最左推导时,语法树由上至下,从左到右生长;最右推导时,语法树从上到下,由右至左生长
语法树与二义性(ambiguity)
一个句子对应的语法树是否唯一?
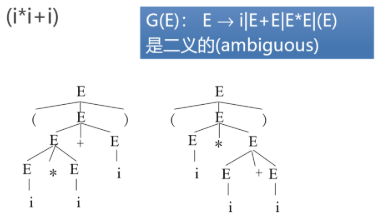
文法的二义性:若一个文法存在某个句子对应两棵不同的语法树,则称这个文法是二义的
上图说明 G(E):E →i|E+E|E*E|(E) 是二义文法
语言的二义性:一个语言是二义的,当它不存在无二义的文法
( 对于语言L,可能文法存在文法G,G’,使得L(G) = L(G’) = L,然而文法G无二义,G’是二义的 )

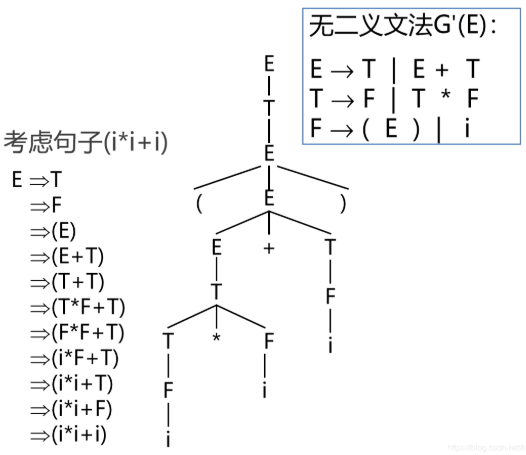
如上图,限制了 * 运算在 + 运算基础上产生,消除了原文法的二义性
二义性问题是不可判定问题,即不存在一个算法,能在有限步骤内,确切地判定一个文法是否是二义的,但可以找到一组无二义文法的充分条件
2019/1/26