状态转换图
状态转换图是一张有限有向图
- 结点表示状态,结点用圆圈表示
- 状态之间存在有向弧,弧上标记有字符或字符集,
表示某一状态接受箭弧上的字符/字符集输入后到达另一状态 - 一张状态转换图中的状态个数是有限的,其中有一个初态,至少有一个终态
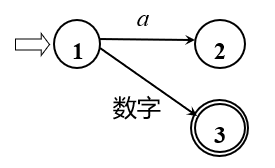
如上图表示状态1为初态,状态3为终态,状态1接受字符a到达状态2,接受数字到达状态3
终态用双圈表示
状态转换图可用于识别 / 接受一定的字符串
若存在一条从初态到某一终态的道路,记这条路上所有弧上的标记符连接成的字(即字符串 )为α,则称α被该状态转换图识别 / 接受
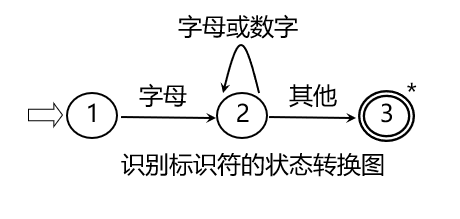
比如上面的状态转换图,可以用来识别以字母开头,可以存在数字的标识符(状态3的*号表示,不包含到状态3的弧上的字符)
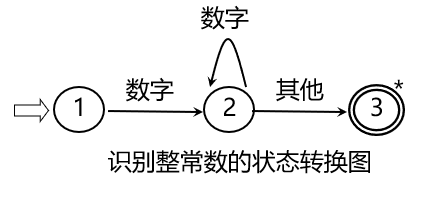
可以识别整常数的状态图
状态转换图在词法分析中的应用
有某种简单的程序设计语言,单词表如下
该语言所有合法的字都在该单词表内描述
| 单词符号 | 种别编码 | 助记符 | 内码值 |
|---|---|---|---|
| DIM | 1 | $DIM | — |
| IF | 2 | $IF | — |
| DO | 3 | $DO | — |
| STOP | 4 | $STOP | — |
| END | 5 | $END | — |
| 标识符 | 6 | $ID | 内部字符串 |
| 常数 | 7 | $INT | 标准二进制形式 |
| = | 8 | $ASSIGN | — |
| + | 9 | $PLUS | — |
| * | 10 | $STAR | — |
| ** | 11 | $POWER | — |
| , | 12 | $COMMA | — |
| ( | 13 | $LPAR | — |
| ) | 14 | $RPAR | — |
可为单词表设计如下状态转移图
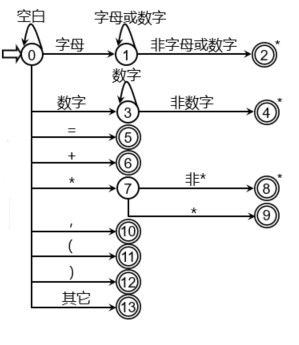
状态2识别关键字和标识符
状态4识别常数
状态5~12识别操作符和括号
状态13为出错状态
那么,可以由此图对该语言的所有代码进行词法分析
词法分析器的实现:状态转换图→程序
使用循环和swith或if,我们很容易把上面的状态转移图实现为词法分析程序
或者使用更巧妙的表驱动方式
| 当前状态 字符 | space | letter | digit | = | + | * | , | ( | ) | 其他 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 3 | 5 | 6 | 7 | 10 | 11 | 12 | 13 |
| 1 | 0 | 1 | 3 | 5 | 6 | 7 | 10 | 11 | 12 | 13 |
| 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 7 | 8 | 8 | 8 | 8 | 8 | 9 | 8 | 8 | 8 | 8 |
设该数组为state
由当前状态cur_state和读取的字符ch
我们可以查表得到下一个状态state[cur_state][ch]
状态转换图与有限自动机
可以用状态转换图等价表示确定有限自动机(DFA) 或者 非确定有限自动机(NFA)
2019/7/20