LeetCode 309. Best Time to Buy and Sell Stock with Cooldown

题目意思大概是给出连续n天的股价，作出如下限制：

1. 只能一次性买入卖出，不能分批交易。分多次买入再卖出或者买入一次然后分多次卖出都是不允许的。
2. 卖出以后有一天的时间不能交易 (one day cooldown time)。

交易次数不限。求可以获得的最大利润。

根据题意，画出DFA如下

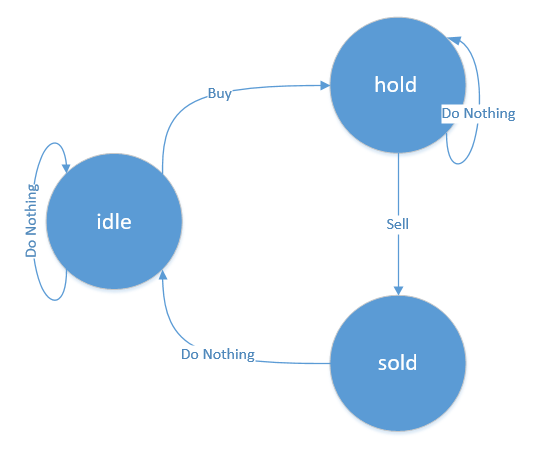
每天可以采取的动作有3种：

1. 什么也不干
2. 买入
3. 卖出

初始状态为idle，手头没有任何股票，且可以进行买入交易。

如果当天或之前有买入动作，则状态为hold，持有股票。

如果当天有卖出动作，则状态变为sold。手头不再持有股票，但也不能买入。

至此，我们可以分别计算3种状态下，采取不同的行动以后各个状态的最大利润。

hold:

前一天为idle，当天买入，或者之前有买入动作，当天什么也不做:

hold = max(idle - prices[i], hold);

idle:

idle可以由之前的idle或sold状态变化而来:

idle = max(idle, sold);

sold:

当天卖出，由hold状态变化而来，注意，当天买入当天卖出是允许的。

sold = hold + prices[i];

最终代码如下：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.empty() || prices.size() <= 1){
            return 0;
        }
        
        int idle = 0, hold = -prices[0], sold = 0;
        for(int i = 1; i < prices.size(); i++){
            hold = max(idle - prices[i], hold);
            idle = max(idle, sold);
            sold = hold + prices[i];
        }
        
        return max(sold, idle);
    }
};