摘要: 本节书摘来华章计算机《算法技术手册》一书中的第2章 ,第2.4.4节, George T.Heineman Gary Pollice Stanley Selkow 著 杨晨 曹如进 译 译更多章节内容可以访问云栖社区“华章计算机”公众号查看。
2.4.4 线性算法的性能
要得到某些问题的解明显需要更多的努力。一个孩子能够计算7 + 5等于12,那么要计算37 + 45会有多难呢?
更具体一点来讲,相加两个n位的数an-1...a0 + bn-1...b0得到一个(n + 1)位的数cn...c0有多难?相加算法使用了如下的原生操作: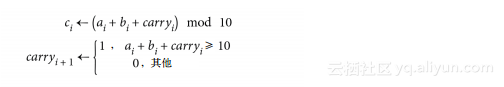
例2-2是相加算法的一个Java实现,其中n位数字使用了一个int数组表示,最高位(即最左边)的数字存放在位置为0的索引上。在本节的例子中,数组中的元素表示一个十进制数d(0≤d≤9) 。
例2-2:相加算法add的Java实现
public static void add (int[] n1, int[] n2, int[] sum) {
int position = n1.length-1;
int carry = 0;
while (position >= 0) {
int total = n1[position] + n2[position] + carry;
sum[position+1] = total % 10;
if (total > 9) { carry = 1; } else { carry = 0; }
position--;
}
sum[0] = carry;
}
只要输入数据能够存储在内存中,add就能够使用两个int数组n1和n2来计算,并将结果保存到sum数组中。例2-3给出了另外一种实现plus,它和add的计算结果完全一样,只是计算过程不同,但是新的实现是否更加高效呢?
例2-3:相加算法plus的Java实现
public static void plus(int[] n1, int[] n2, int[] sum) {
int position = n1.length;
int carry = 0;
while (--position >= 0) {
int total = n1[position] + n2[position] + carry;
if (total > 9) {
sum[position+1] = total-10;
carry = 1;
} else {
sum[position+1] = total;
carry = 0;
}
}
sum[0] = carry;
}
这个小改动会影响算法的性能吗?让我们考虑其他两个影响算法性能的潜在因素:
add和plus都能够很容易地转换成C程序。那么,编程语言的选择是如何影响算法性能的?
程序可以在不同的计算机上执行。那么,计算机硬件的选择是如何影响算法性能的?
上述Java实现总共执行了10 000次相加实验,其中相加数字的位数从256位到32 768位不等。对于每个数位长度,都会有对应长度的随机数生成。之后,对于每次实验,这两个数都会循环移位(一个向左,另一个向右),以产生两个不同的数进行相加。我们使用了两种不同的编程语言(C和Java)实现算法。我们一开始假设的是随着数据规模的加倍,算法执行时间也会加倍,正好借此实验来确认算法的总体行为是否与计算机、编程语言以及实现无关。每一种算法实现均采用了一系列的编译选项,包括:
g
使用附带调试信息的C语言版本编译。
O1,O2,O3
C程序会按照不同的优化等级进行编译。数字越高意味着性能越好。
Java
算法的Java 版实现。
表2-3给出了add与plus的实验结果。第8列和最后一列对比了plus在问题规模为2n和规模为n时的性能比率。t(n)为加法算法在给定规模n下的实际执行时间。表中的增长模式显示了plus算法在计算两个n位的整数时所需要的时间。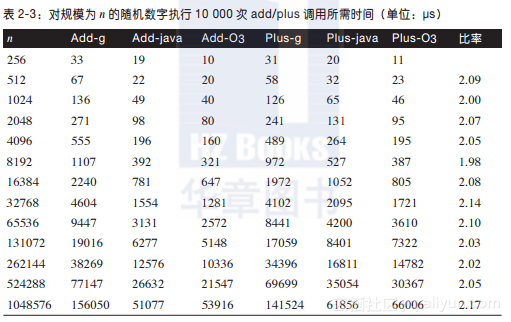
加法算法是与输入规模呈线性关系的。也就是说,对于“足够大”的n,即n > n0时,存在一个常数c > 0,满足t(n)≥c*n。我们并不需要计算c或者n0的值,而只要知道它们是真实存在的并且可以计算出来即可。一个争论的焦点是,在做加法时,每一位都必须被检查(考虑漏掉一位的后果),这样的复杂程度是否需要一个线性时间下界。
对于所有的plus操作(不管采用什么编程语言或者编译配置),c为1/7,n0为256。其他的加法实现应该会有不同的常数,但是它们的总体表现仍然呈线性。这个结果让那些认为整数算术是常数操作的程序员大吃一惊。不过,当整数的位数固定(例如16 位或者64 位)时,我们可以认为加法是常数时间。
在考虑算法之间的差异时,了解算法的增长率比常数c更为重要。看似无关紧要的差异可能就会导致不同的性能。加法算法的plus实现试图通过消除取模计算(%)来提升算法效率。尽管如此,在plus和add都采用-O3优化时,add还是要比plus实现快30%。当然,这并不是说可以忽略掉常数c的值。如果做大量的加法,那么c的一点点小变动都会对程序的性能产生很大的影响。