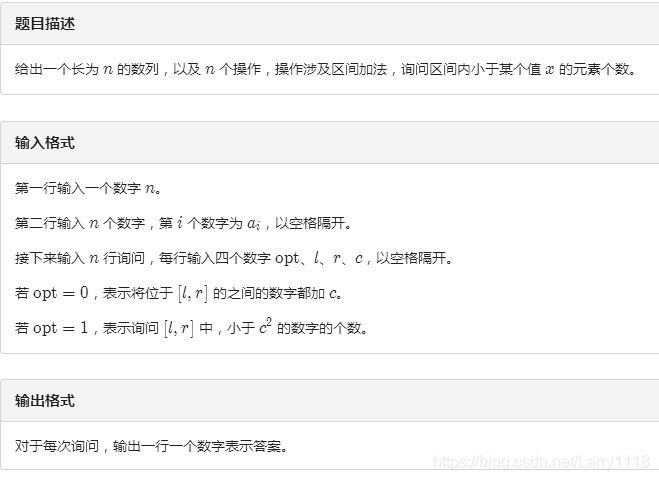
这题,呜呜呜。。。。
我™改了™的好几天啊啊啊啊啊!!!!!
这题依旧分块。原序列设为a[]
对于每个块,我们可以用另一个数组排序(在此设为d[])。
另一个!!!
(我不知道为什么,将原序列记录了位置在排序™还是错了。。。)
然后,还是分类讨论。
opt==0
分成三块。
1:l所在的凸出来的那一部分,暴力搞,然后将a[]中l的块暴力赋给d[],并排序。
2:r所在的凸出来的那一部分,方法同上。
3:中间的整个的一些块,由于不影响其单调性,所以我们可以设个b[]来加。
当然,如果l和r在同一个块中的话要特判!
opt==1
分成三块。
1:l所在的凸出来的那一部分,暴力搞。
2:r所在的凸出来的那一部分,方法同上。
3:中间的整个的一些块,由于单调,可以二分来求每一块中符合的个数。
当然,如果l和r在同一个块中的话要特判!
嗯嗯,大概就这些了。
上标:
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
int a[50010],d[50010],n,b[231];
int opt,l,r,c,st;
int bl[50010],le[231],ri[231];
inline int read()
{
int x=0,f=0; char c=getchar();
while (c<'0' || c>'9') f=(c=='-') ? 1:f,c=getchar();
while (c>='0' && c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
return f ? -x:x;
}
void update(int x)
{
for (int i=le[x];i<=ri[x];i++) d[i]=a[i];
sort(d+le[x],d+ri[x]+1);
}
void add(int l,int r,int c)
{
for (int i=l;i<=min(ri[bl[l]],r);i++) a[i]+=c;
update(bl[l]);
if (bl[l]!=bl[r])
{
for (int i=le[bl[r]];i<=r;i++) a[i]+=c;
update(bl[r]);
}
for (int i=bl[l]+1;i<=bl[r]-1;i++) b[i]+=c;
}
int query(int l,int r,int c)
{
int ans=0;
for (int i=l;i<=min(ri[bl[l]],r);i++)
if (a[i]+b[bl[l]]<c) ans++;
if (bl[l]!=bl[r])
{
for (int i=le[bl[r]];i<=r;i++)
if (a[i]+b[bl[r]]<c) ans++;
}
for (int i=bl[l]+1;i<=bl[r]-1;i++)
{
int L=le[i],R=ri[i],mid,s=0;
while (L<=R)
{
mid=L+R>>1;
if (d[mid]+b[i]<c) s=mid,L=mid+1;
else R=mid-1;
}
if (s) ans+=s-le[i]+1;
}
return ans;
}
int main()
{
freopen("6278.in","r",stdin);
freopen("6278.out","w",stdout);
n=read();st=sqrt(n);
for (int i=1;i<=n;i++) a[i]=d[i]=read();
for (int i=1;i<=n;i++)
{
bl[i]=(i-1)/st+1;
if (!le[bl[i]]) le[bl[i]]=i;
ri[bl[i]]=i;
}
for (int i=1;i<=bl[n];i++)
sort(d+le[i],d+ri[i]+1);
for (int i=1;i<=n;i++)
{
opt=read(),l=read(),r=read(),c=read();
if (opt==0) add(l,r,c);
else printf("%d
",query(l,r,c*c));
}
return 0;
}