sklearn中的回归器性能评估方法(转)

• explained_variance_score()
• mean_absolute_error()
• mean_squared_error()
• r2_score() 

以上四个函数的相同点：

• 这些函数都有一个参数“multioutput”，用来指定在多目标回归问题中，若干单个目标变量的损失或得分以什么样的方式被平均起来
• 它的默认值是“uniform_average”，他就是将所有预测目标值的损失以等权重的方式平均起来
• 如果你传入了一个shape为（n_oupputs,）的ndarray，那么数组内的数将被视为是对每个输出预测损失（或得分）的加权值，所以最终的损失就是按照你锁指定的加权方式来计算的
• 如果multioutput是“raw_values”,那么所有的回归目标的预测损失或预测得分都会被单独返回一个shape是（n_output）的数组中

explained_variance_score

#explained_variance_score
from sklearn.metrics import explained_variance_score
y_true=[3,-0.5,2,7]
y_pred=[2.5,0.0,2,8]
print(explained_variance_score(y_true,y_pred))
y_true=[[0.5,1],[-1,1],[7,-6]]
y_pred=[[0,2],[-1,2],[8,-5]]
print(explained_variance_score(y_true,y_pred,multioutput="raw_values"))
print(explained_variance_score(y_true,y_pred,multioutput=[0.3,0.7]))

#结果
#0.957173447537
#[ 0.96774194  1.        ]
#0.990322580645

mean_absolute_error

#mean_absolute_error
from sklearn.metrics import mean_absolute_error
y_true=[3,0.5,2,7]
y_pred=[2.5,0.0,2,8]
print(mean_absolute_error(y_true,y_pred))

y_true=[[0.5,1],[-1,1],[7,-6]]
y_pred=[[0,2],[-1,2],[8,-5]]
print(mean_absolute_error(y_true,y_pred))
print(mean_absolute_error(y_true,y_pred,multioutput="raw_values"))
print(mean_absolute_error(y_true,y_pred,multioutput=[0.3,0.7]))

#结果
#0.5
#0.75
#[ 0.5  1. ]
#0.85

mean_squared_error

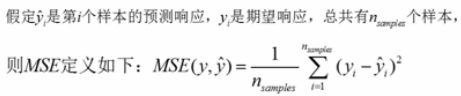
#mean_squared_error
from sklearn.metrics import mean_squared_error
y_true=[3,-0.5,2,7]
y_pred=[2.5,0.0,2,8]
print(mean_squared_error(y_true,y_pred))
y_true=[[0.5,1],[-1,1],[7,-6]]
y_pred=[[0,2],[-1,2],[8,-5]]
print(mean_squared_error(y_true,y_pred))

#结果
#0.375
#0.708333333333

median_absolute_error

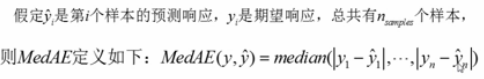
#median_absolute_error
from sklearn.metrics import median_absolute_error
y_true=[3,-0.5,2,7]
y_pred=[2.5,0.0,2,8]
print(median_absolute_error(y_true,y_pred))

#结果
#0.5

r2_score

 

#r2_score
from sklearn.metrics import r2_score
y_true=[3,-0.5,2,7]
y_pred=[2.5,0.0,2,8]
print(r2_score(y_true,y_pred))

y_true=[[0.5,1],[-1,1],[7,-6]]
y_pred=[[0,2],[-1,2],[8,-5]]
print(r2_score(y_true,y_pred,multioutput="variance_weighted"))

y_true=[[0.5,1],[-1,1],[7,-6]]
y_pred=[[0,2],[-1,2],[8,-5]]
print(r2_score(y_true,y_pred,multioutput="uniform_average"))
print(r2_score(y_true,y_pred,multioutput="raw_values"))
print(r2_score(y_true,y_pred,multioutput=[0.3,0.7]))

#结果
#0.948608137045
#0.938256658596
#0.936800526662
#[ 0.96543779  0.90816327]
#0.92534562212