排序算法----堆排序

堆排序算法使用二叉堆实现排序，树上的每一个节点对应数组中的一个元素。

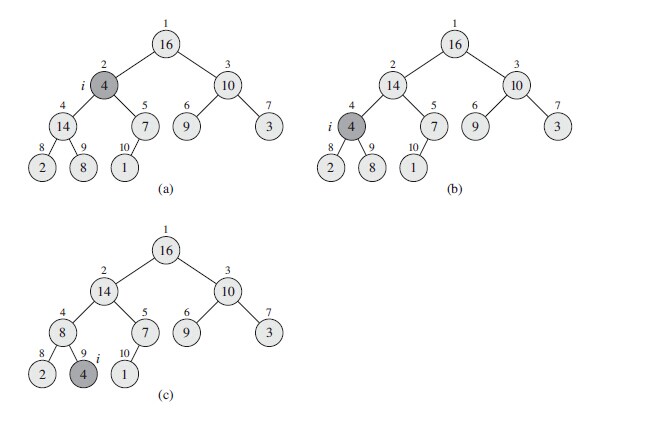
第一步：使用MAX_HEAPIFY维护一个最大堆（所有孩子节点都必须小于或等于其父节点）。它的输入为一个数组A和一下标i,调用MAX_HEAPIFY时，假设节点i的左右子树都是最大堆。

伪码：

LEFT(i)
  return 2i

RIGHT(i)
  return 2i+1

MAX_HEAPIFY(A,i)
  
l = LEFT(i)

r = RIGHT(i)

if l <=A.heap-size and A[l] > A[i]

    largest = l

else

    largest = i

if r<= A.heap-size and A[r] > A[largest]

   largest = r

if largest != i

    exchange A[i] with A[largest]

   MAX_HEAPIF(A,largest)

 假设节点i的左子数和右子数都是最大堆。程序首先找出节点i，它的左孩子节点和右孩子节点中最大的一个，如节点i是最大，那么以i为根节点二叉堆就是最大堆了程序结束；否则，交换节点i和最大那个节点largest，于是以largest为根节点的二叉树就有可能违反了最大堆的性质，因此以largest为下标递归调用MAX_HEAPIFY。

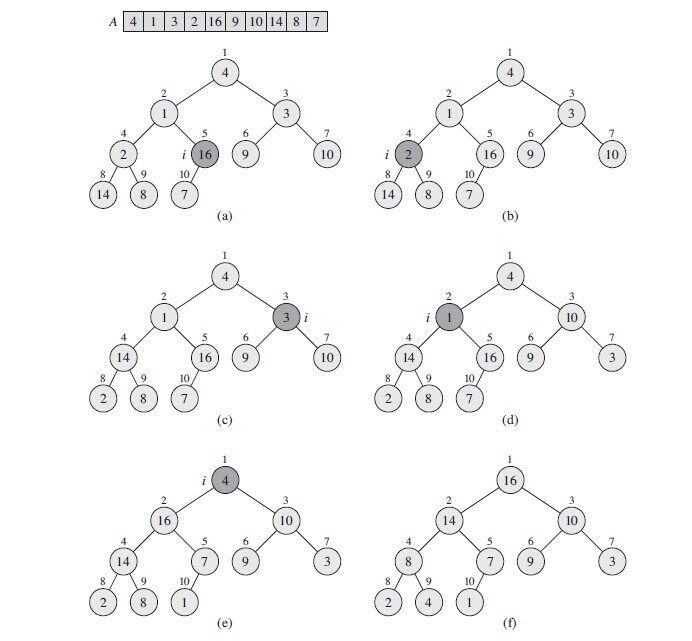
第二步：使用BUILD_MAX_HEAP(A)建立一个最大堆。

伪码：

BUILD-MAX_HEAP(A)

A.heap-size = A.length

for i = ⌊A.length / 2⌋   downto 1

   MAX_HEAPIFY(A,i) 

从底向上的方法利用MAX_HEAPIFY把长度为n的数组A转换为一个最大堆。这里我们不用从数组A的最后一个元素开始调用MAX_HEAPIFY，可以证明：从⌊n/2⌋ + 1 到n中的元素都是数的叶节点（没有孩子节点），所以我们从⌊n/2⌋到1调用MAX_HEAPIFY，转换A成为一个最大堆.

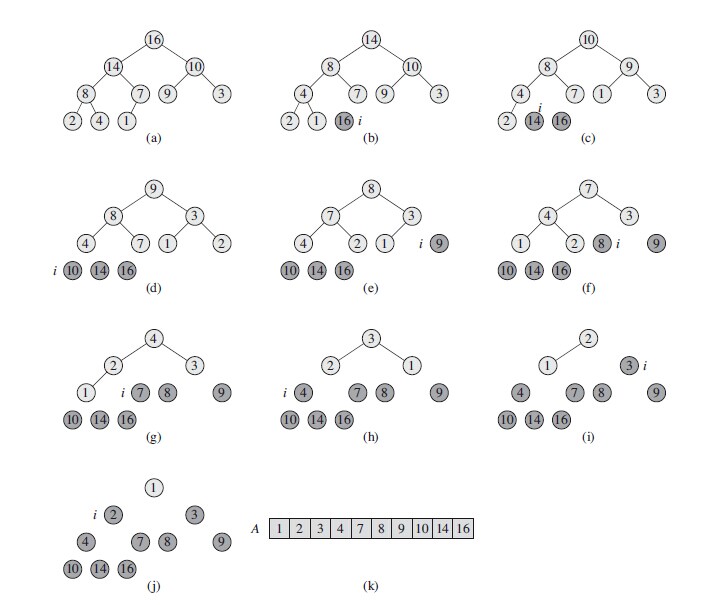
第三步：使用BUILD_MAX_HEAP 和 MAX_HEAPIFY完成堆排序算法HEAPSORT

伪码：

HEAPSORT(A)

BUILD-MAX-HEAP(A)

for i = A.length downto 2

    exchange A[1]  with A[i]

    A.heap-size = A.heap-size - 1

   MAX-HEAPIFY(A,1)

 首先：利用BUILD_MAX_HEAP 把传入的数组A转换为一个最大堆，在最大堆中，根节点为所有节点中最大的；

 然后：交换二叉堆根节点A[1]和最后一个节点A[n]，这时数组中的最大的值被交换到数组的最后；把最后一个节点从堆中去掉，利用MAX_HEAPIFY从新维护数组A[1],A[n -1]为一个最大堆

  最后：循环上面步骤,把依次最大的值放到数组末尾，直到堆的大小降到2

时间复杂度：HEAPSORT过程的时间复杂度是O(nlgn),每次调用BUILD_MAX_HEAP的时间复杂度是O(n),n-1次调用MAX_HEAPIFY，每次时间为O(lgn)；

C++代码：

#define   LEFT(i)   (2 * (i + 1) - 1)
#define   RIGHT(i)  (2 * (i + 1))

#define   EXCHANGE(a,b) (a) = (a) + (b);
                                        (b) = (a) - (b);
                                        (a) = (a) - (b)

void MAX_HEAPIFY(int A[],int i,int heap_size)
{
    int l = LEFT(i);
    int r = RIGHT(i);
    int largest = -1;

    if(l <= heap_size && A[l] > A[i])
    {
        largest = l;
    }
    else
    {
        largest = i;
    }

    if(r <= heap_size && A[r] > A[largest])
    {
        largest = r;
    }

    if(largest != i)
    {
        EXCHANGE(A[i],A[largest]);
        MAX_HEAPIFY(A,largest,heap_size);
    }
}

void BUILD_MAX_HEAP(int A[],int heap_size)
{
    for(int i = heap_size / 2;i >=0;--i)
    {
        MAX_HEAPIFY(A,i,heap_size);
    }
}

//堆排序，T(n) = O(nlgn) 
void HEAPSORT(int A[],int heap_size)
{
    BUILD_MAX_HEAP(A,heap_size);
    for(int i = heap_size;i > 0;--i)
    {
        EXCHANGE(A[heap_size],A[0]);
        heap_size -= 1;
        MAX_HEAPIFY(A,0,heap_size);
    }
}