这是啥?
先上链接
exe附源码一份
链接: https://pan.baidu.com/s/1VQ6zlxCDqsGMtEuMc7bynA 提取码: fx6z
C版本

Python版,GUI界面
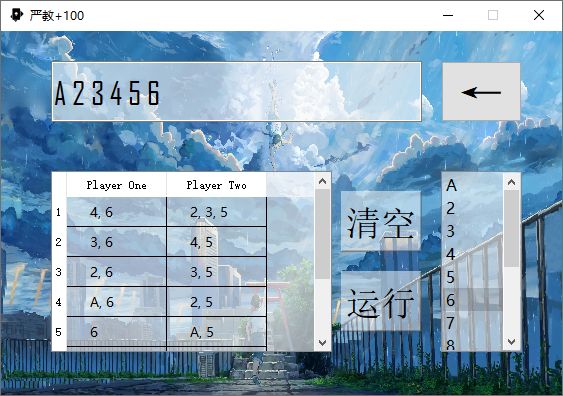
问题来了,标题是什么意思
(以下皆C语言版本,python版本源码在github,上面已给出)

严教:简单的说就是 拿n张牌,从这n张牌里分出两组任意数量的牌,加起来总和相等的话就能给玩家
前几天玩三国杀,朋友抽了个张菖蒲出来,一开始还好,就拿4张牌让我算,差不多看一眼就出答案了
直到有一次他掏出8张牌,1分钟的技能持续时间,我硬是一种都没算出来。一气之下写了个程序来算
把这个技能转换成算法题就是这个意思:

在游戏里追求牌多,所以同样的点数和就只输出了一种
算法分析
因为是写来在游戏里用的,以轻量级为主,我这里使用C语言编写
- 不多说,上来就是导入stdio
#include<stdio.h>
-
这题第一眼看过去就能想到是一种排列组合。不过先别急,分析一下先。要在n张牌里分出两组牌,令第一组牌为A,第二组为B
首先要搞清楚,并不是所有的牌都参与到分组中,也就是说可以有多余的牌,那么A与B的关系就不是简单的A+B=n了,所以A和B两组牌是分别进行的排列组合。
解决排列组合最方便的算法应该就是深搜了,如果对深搜不熟悉或者没听过的话可以去CSDN搜索(dfs、深度优先搜索)。CSDN上有很多关于深搜的讲解
-
既然清楚了是两个排列组合,那么就决定使用两个深搜。先定义几个全局变量
#define MAXLENTH 16 // 全局变量 int a[MAXLENTH] = { 0 }; // 输入数组 int b[MAXLENTH] = { 0 }; // 0-未出现 1-第一组 2-第二组 int c[10000] = { 0 }; // 记录sum int sum1 = 0; int sum2 = 0; int n; int k = 0; // c数组下标 int t = 1; // 深度1 int t2 = 1; // 深度2 // 函数声明 void dfs(int i, int x); // 深搜-第一组 void dfs2(int i, int x); // 深搜-第二组 void pt(); // 输出- MAXLENTH -> 自定义的输入最大长度
- a数组 -> 输入数据
- b数组 -> a数组中各个数据的状态
- c数组 -> 已出现过的牌堆和
- sum1 -> 牌堆1的点数和
- sum2 -> 牌堆2的点数和
- n -> 输入数据个数
- k -> 当前c数组长度
- t / t2 -> 两个深搜函数的最大到达深度
这里先不解释这些变量的作用,能看懂当我没说,我也觉得我写的好乱,应该是那时候太急了。
-
先来看输入函数pt
void pt() { int x = 1; for (int i = 0; i < 2; i++) { for (int j = 0; j < n; j++) if (b[j] == x) printf("%d ", a[j]); printf(" "); x++; } printf(" "); }为什么
i是0到1? (*`д´*) 这都看不出来是输出两组数吗那
j呢?j不就是遍历数组吗x是什么,x是状态,定义变量的时候注释了b数组的3中状态,x就是特定的一种状态,当x等于1的时候, 也就是i等于0的那次循环,输出b[j]等于1的a[j],也就是第一组数据然后
x++,在输出第二组数应该不难理解,这里提一下就是先知道
b[j]的3种状态分别表示什么 -
接下来看看深搜部分。理解题目之后应该清楚,在例子
1 2 3 4 5 6中,3与1 2是一对,4 6和2 3 5也是一对,所以两组数各自的长度是未知的,可以是一个数、两个数、三个数……那么我们每次排列组合当然需要一个深度咯
int t = 1; // 深度1 int t2 = 1; // 深度2开头定义的两个全局变量
tt2分别就是两个深搜的深度假设有n个数,那么开始
tt2都是1,也就是只有一层深度,两组数都是只有一个数,分别都是遍历了整个a数组,而且不能重复还是看图直观吧
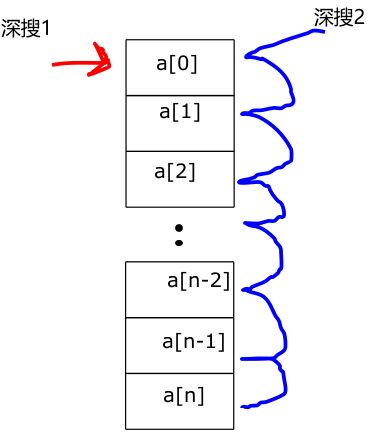
第一个深搜一个一个慢慢遍历,深搜1每次指向一个数的时候深搜2都要跑一遍整个数组,每一次都判断总和是否相等,当然如果某个数已经被选中了就不选了(也就是b数组对应的下标不是0了)。
否则的话就选中(更改b数组中的这个位置的数为1或者2,1就是第一组,2就是第二组)
当然图里红线蓝线都经过了a[0],不是画错了,因为遍历可不管你这个位置b是多少,只有判断才管
像这样蓝线走完一次之后,红色箭头像下走一格,然后蓝线继续老操作。
是不是很简单,但是这才第一层
如果我第二组要两个数呢
还是画个图
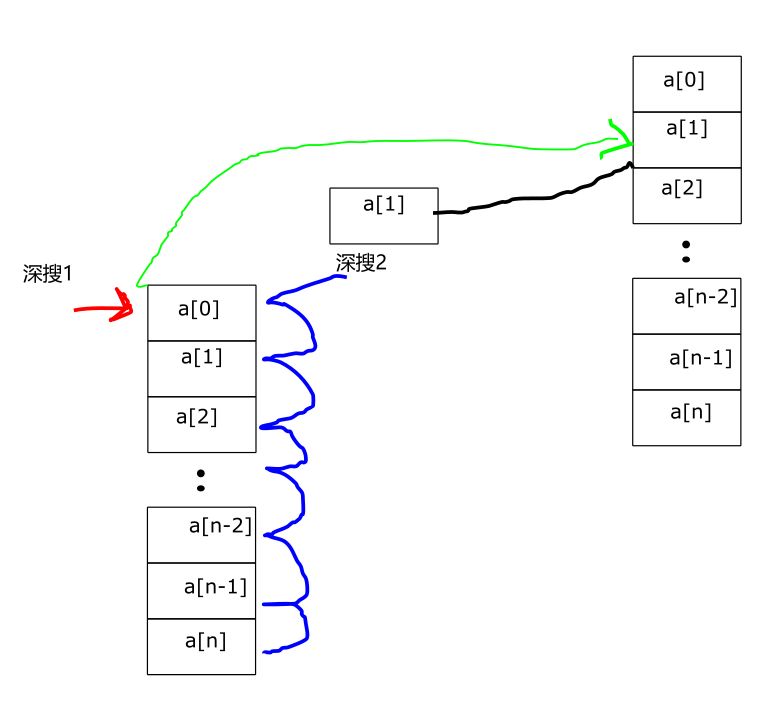
第一组还是一个数,所以还是老的做法,红色箭头每指向一个新的数,绿色箭头要依次遍历a数组,并取出这个数来作为第二组的其中一个数,然后进行第二次深搜,也就是蓝线
这么说可能有点难理解,换个形式就是
for(){
for(){
}
}
这样的嵌套遍历,第一个for取一个数,第二for也取一个数
这两个不同的数共同作为第二组数
如果你不懂深搜可能要问了,那为什么不直接用for?深搜是什么?
别急,这里还只是1-2(下面都这样表示两组数分别的数量,左边表示第一组的数,右边表示第二组)
首先我们要明确一点,for循环是定死的,获取可以用break来减少循环,但你总不能增加循环吧。
写了4个for运行能来5个for?
其次,基数小的时候确实写for方便,但数量一大呢,例如我开头说的给我了8张牌,4-4甚至1-7的时候呢,写7个循环?不现实吧。
所以我们要用深搜
直接上代码
void dfs(int i, int x) {
if(x == t){
return;
}
while (i < n) {
if (b[i] == 0) {
b[i] = 1;
sum1 += a[i];
dfs(i + 1, x + 1);
b[i] = 0;
sum1 -= a[i];
}
i++;
}
};
这是一个最典型的深搜,当然我还没加一些别的条件
仅仅是对一组数排列组合
第一个if不用说了,就是深度(也就是递归跳出条件)
i就是当前遍历的下标
while中如果当前下标没被选择那么就选中它并且表明是1(第一组),同时使这一组数的和sum1加上这个数,然后继续调用自身进行搜索,出来之后也就是要换目标了,于是让这个位置的b重置为0,表示未选中,再让sum1减去这个数
这就是个简单的排列组合,所以第二组的深搜也同样可以调用这个模块
void dfs(int i, int x) {
if (x == t) {
for (int j = 1; j <= n - t; j++) {
sum2 = 0;
t2 = j;
dfs2(0, 0);
}
return;
}
// 模块
while (i < n) {
if (b[i] == 0) {
b[i] = 1;
sum1 += a[i];
dfs(i + 1, x + 1);
b[i] = 0;
sum1 -= a[i];
}
i++;
}
};
void dfs2(int i, int x) {
if (x == t2) {
if (sum1 == sum2) {
int m;
for (m = 0; m <= k; m++)
if (c[m] == sum1) break;
if (m >= k) {
c[k] = sum1;
k++;
printf("第%d种
", k);
pt();
}
}
return;
}
// 模块
while (i < n) {
if (b[i] == 0) {
b[i] = 2;
sum2 += a[i];
dfs2(i + 1, x + 1);
b[i] = 0;
sum2 -= a[i];
}
i++;
}
}
上面我已经把相同的模块标注出来了,要注意的是里面的部分变量要修改成对应的变量
下面来看他们不同的部分
dfs ( 第一组 ) 中:
if (x == t) {
for (int j = 1; j <= n - t; j++) {
sum2 = 0;
t2 = j;
dfs2(0, 0);
}
return;
}
x 等于t时也就是到达当前最大深度时执行这些代码
for循环从1到n-t,n-t就是剩下几个数,所以第二个深搜的深度可以从1到n-t,每一次循环重置sum2并且改变t2,调用第二组的深搜。
应该不难理解,就是以第一组为主,第一组每找到一种排列组合,就要让第二组找出他的所有排列组合情况
dfs2 ( 第二组 ) 中:
if (x == t2) {
if (sum1 == sum2) {
int m;
for (m = 0; m <= k; m++)
if (c[m] == sum1) break;
if (m >= k) {
c[k] = sum1;
k++;
printf("第%d种
", k);
pt();
}
}
return;
}
x等于t2,第二组的深搜到达当前最大深度,要知道我们前置条件就是第一组已经到达最大深度,所以这时候就可以开始比较了。
如果两个sum相等的话,首先当然要遍历c数组看看有没有这个和,如果有就直接跳过了,没有的话继续执行下面的代码。
注意k是全局变量,我们不动他的时候他就是个定值,用来表示c数组的长度在合适不过了
话题回来,如果还没有过这个和,那么就向c数组中添加这个值,并且输出。
-
两个函数部分就到这里结束了,细心的话能发现目前为止我们的第一组始终只有一个数,因为我们的
t没变过这个实现方法很多,我是写在主函数中,所以放到了最后
int main() { while(1){ printf("输入n ( 0结束 ): "); scanf("%d", &n); if (!n) break; printf("输入数字序列:"); for (int i = 0; i < n; i++) { scanf("%d", &a[i]); } /************************/ for (int i = 1; i <= n; i++) { sum1 = 0; t = i; dfs(0, 0); } /************************/ // 初始化 for (int i = 0; i <= k; i++) { c[i] = 0; k = 0; } for (int i = 0; i <= n; i++) { a[i] = 0; b[i] = 0; } } }*号包围起来的部分就是不断的改变
t的值来使第一组数的数量发生变化,不多讲了其他部分的代码应该也不难懂。
讲解就到这了,下面附上完整代码
完整代码
#include<stdio.h>
int a[16] = { 0 }; // 输入数组
int b[16] = { 0 }; // 0-未出现 1-第一组 2-第二组
int c[10000] = { 0 }; // 记录sum
int sum1 = 0;
int sum2 = 0;
int n;
int k = 0; // c数组下标
int t = 1; // 深度1
int t2 = 1; // 深度2
void dfs(int i, int x); // 深搜-第一组
void dfs2(int i, int x); // 深搜-第二组
void pt(); // 输出
int main() {
while(1){
printf("输入n ( 0结束 ): ");
scanf("%d", &n);
if (!n) break;
printf("输入数字序列:");
for (int i = 0; i < n; i++) {
scanf("%d", &a[i]);
}
for (int i = 1; i <= n; i++) {
sum1 = 0;
t = i;
dfs(0, 0);
}
// 初始化
for (int i = 0; i <= k; i++) {
c[i] = 0;
k = 0;
}
for (int i = 0; i <= n; i++) {
a[i] = 0;
b[i] = 0;
}
}
}
void dfs(int i, int x) {
if (x == t) {
for (int j = 1; j <= n - t; j++) {
sum2 = 0;
t2 = j;
dfs2(0, 0);
}
return;
}
while (i < n) {
if (b[i] == 0) {
b[i] = 1;
sum1 += a[i];
dfs(i + 1, x + 1);
b[i] = 0;
sum1 -= a[i];
}
i++;
}
};
void dfs2(int i, int x) {
if (x == t2) {
if (sum1 == sum2) {
int m;
for (m = 0; m <= k; m++)
if (c[m] == sum1) break;
if (m >= k) {
c[k] = sum1;
k++;
printf("第%d种
", k);
pt();
}
}
return;
}
while (i < n) {
if (b[i] == 0) {
b[i] = 2;
sum2 += a[i];
dfs2(i + 1, x + 1);
b[i] = 0;
sum2 -= a[i];
}
i++;
}
}
void pt() {
int x = 1;
for (int i = 0; i < 2; i++) {
for (int j = 0; j < n; j++)
if (b[j] == x) printf("%d ", a[j]);
printf("
");
x++;
}
printf("
");
}