17.1 聚合分析
用来确定一个n个操作的序列的总代价的上界T(n).
- 由n个push,pop,multi-pop组成的操作序列。依赖于push
- 二进制计数器递增
A[0]每次都翻转,A[1]每两次翻转一次,A[2]每两次翻转一次...
17.2 核算法
较早操作的余额(overcharge)作为预付信用(prepaid credit)储存起来,与数据结构中的特定对象相关联。对应后续操作中摊还代价小于实际代价的情况,信用可以用来支付差额。
17.3 势能法
势能法摊还分析并不将预付代价表示为数据结构中特定对象的信用,而是表示为“势能”,或简称“势”,将势能释放即可用来支付未来操作的代价。我们将势能与整个数据结构而不是特定对象相关联。
工作方式如下:
我们将对一个初始数据结构D0执行n个操作。对每个i=1,2,。。。,n,令ci为第i个操作的实际代价,令Di为在数据结构Di-1上执行第i个操作得到的的结果数据结构。势函数Φ将每个数据结构Di映射到一个实数Φ(Di),此值即为关联到数据结构Di的势。第i个操作的摊还代价c‘i用势函数Φ定义为
c‘i=ci+Φ(Di)-Φ(Di-1)
总摊还代价为
![]()
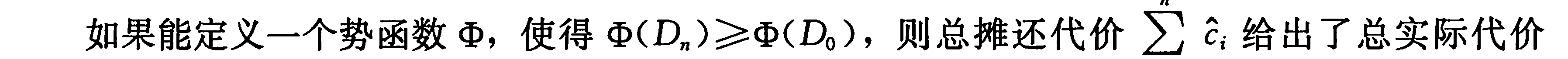
![]()
栈操作:可定义栈的势为栈中的对象数量。
二进制计数器:可定义计数器的势为其中1的位数。
17.4 动态表
17.4.1 表扩张
17.4.2 表扩张和收缩
总之,由于每个操作的摊还代价的上界是一个常数,在一个动态表上执行任意n个操作的实际运行时间是O(n)。