PAT（甲级）2021年春季考试

7-1 Arithmetic Progression of Primes (20 分)

时间限制：1000 ms 内存限制：64 MB

In mathematics, an arithmetic progression (AP，等差数列) is a sequence of numbers such that the difference between the consecutive terms is constant. In 2004, Terence Tao (陶哲轩) and Ben Green proved that for any positive n, there exists at least one arithmetic progression consists of n consecutive prime numbers. For example, { 7，37，67，97，127，157 } is one solution for n=6. Now it is your job to find a maximum solution for a given n within a given range.

Input Specification:

Each input file contains one test case, which gives two positive integers in a line: n (≤10), the number of consecutive prime terms in an arithmetic progression, and MAXP (2≤MAXP<10⁵), the upper bound of the largest prime in the solution.

Output Specification:

For each test case, if there exists a solution, print in ascending order the prime numbers in a line. If the solution is not unique, output the one with the maximum common difference. If there is still a tie, print the one with the maximum first number. If there is no solution bounded by MAXP, output the largest prime in the given range instead.

All the numbers in a line must be separated by a space, and there must be no extra space at the beginning or the end of the line.

Sample Input 1:

5 1000

Sample Output 1:

23 263 503 743 983

Sample Input 2:

10 200

Sample Output 2:

199

解析：

看到这1秒的限时就知道这题不简单……

题目大意：找出一个全为质数的等差数列（公差为正），使得项数为给定的n，且末项不超过给定的MAXP。如果有多个解，输出公差最大（第一判断条件）且首项最大（第二判断条件）的。如果无解，输出小于等于MAXP的最大质数。

1、由于MAXP<10⁵，可以直接用埃氏筛法打表；

2、既然求公差最大且首项最大的解，那么末项一定最大。进行搜索的时候，用两层循环，外循环从大到小遍历公差，内循环从大到小遍历末项，找到的第一个满足条件的等差数列就是解。先找到小于等于MAXP的最大质数last作为最大末项，再求公差的搜索范围：最大公差为(last - 2) / (n - 1)，例如样例1给出n=5, MAXP=1000，求出last为997，那就是把[2, 997]的范围分成4份并去尾，得最大公差为248。显然，最小公差为1。有了公差，末项的搜索范围就得到了：(last - 当前公差, last]。这样得到的第一个满足条件的解即为答案。

3、特判n为1的情形。

#include <iostream>
using namespace std;

const int maxn = 100002;

int isPrime[maxn], N;  // isPrime中0表示为质数，1表示不为质数

// 埃氏筛法
void getPrimes () {
    int i, j;
    for (i = 2; i < maxn; i++) {
        if (isPrime[i] == 0) {
            for (j = i + i; j < maxn; j += i) isPrime[j] = 1;
        }
    }
}

// 检查对应末项和公差的数列是否满足要求
bool check (int last, int diff) {
    int number = last;
    for (int i = 0; i < N; i++) {
        if (number < 2 || isPrime[number] == 1) return false;
        number -= diff;
    }
    return true;
}

void test () {
    int MAXP, i, j, k;
    scanf("%d %d", &N, &MAXP);
    getPrimes();
    isPrime[0] = isPrime[1] = 1;
    // 找到最大质数
    for (i = MAXP; i >= 2; i--) if (isPrime[i] == 0) break;
    if (N == 1) {
        printf("%d", i);
        return;
    }
    int last = i;  // 存最大质数
    int diff = (last - 2) / (N - 1);  // 最大公差
    for (j = diff; j >= 1; j--) {  // 公差
        for (i = last; i > last - j; i--) {  // 末项
            if (check(i, j)) {
                // 输出解
                for (k = 0; k < N; k++) {
                    printf("%d", i - j * (N - k - 1));
                    if (k < N - 1) printf(" ");
                }
                return;
            }
        }
    }
    printf("%d", last);
}

int main () {
    test();
    return 0;
}

7-2 Lab Access Scheduling (25 分)

时间限制：200 ms 内存限制：64 MB

Nowadays, we have to keep a safe social distance to stop the spread of virus due to the COVID-19 outbreak. Consequently, the access to a national lab is highly restricted. Everyone has to submit a request for lab use in advance and is only allowed to enter after the request has been approved. Now given all the personal requests for the next day, you are supposed to make a feasible plan with the maximum possible number of requests approved. It is required that at most one person can stay in the lab at any particular time.

Input Specification:

Each input file contains one test case. Each case starts with a positive integer N (≤2×103), the number of lab access requests. Then N lines follow, each gives a request in the format:

hh:mm:ss hh:mm:ss

where hh:mm:ss represents the time point in a day by hour:minute:second, with the earliest time being 00:00:00 and the latest 23:59:59. For each request, the two time points are the requested entrance and exit time, respectively. It is guaranteed that the exit time is after the entrance time.

Note that all times will be within a single day. Times are recorded using a 24-hour clock.

Output Specification:

The output is supposed to give the total number of requests approved in your plan.

Sample Input:

7
18:00:01 23:07:01
04:09:59 11:30:08
11:35:50 13:00:00
23:45:00 23:55:50
13:00:00 17:11:22
06:30:50 11:42:01
17:30:00 23:50:00

Sample Output:

5

Hint:

All the requests can be approved except the last two.

解析：

区间贪心。将各组时间转成秒，按离开时间从小到大排序，第一个请求（最早离开的）予以批准，之后每一个请求，如果与上一次批准的区间有重叠就不予批准，直到出现一个不重叠的，批准，以此类推。

#include <vector>
#include <algorithm>
#include <iostream>

using namespace std;

int time2int (string& s) {
    int ans1 = 0;
    ans1 = (stoi(s.substr(0, 2)) * 3600 + stoi(s.substr(3, 2)) * 60 + stoi(s.substr(6, 2)));
    return ans1;
}

typedef struct Node {
    int a, b;
    Node (int a, int b) : a(a), b(b) {}
} Node;

bool cmp (Node a, Node b) {
    return a.b < b.b;
}

vector<Node> nodes;

void test () {
    int n, i, j;
    string s1, s2;

    scanf("%d", &n);
    for (i = 0; i < n; i++) {
        cin >> s1 >> s2;
        nodes.push_back(Node(time2int(s1), time2int(s2)));
    }
    sort(nodes.begin(), nodes.end(), cmp);
    int count = 1, last = 0;
    for (i = 1; i < n; i++) {
        if (nodes[i].a >= nodes[last].b) {
            count++;
            last = i;
        }
    }
    printf("%d", count);
}

int main () {
    test();
    return 0;
}

7-3 Structure of Max-Heap (25 分)

时间限制：400 ms 内存限制：64 MB

In computer science, a max-heap is a specialized tree-based data structure that satisfies the heap property: if P is a parent node of C, then the key (the value) of P is greater than or equal to the key of C. A common implementation of a heap is the binary heap, in which the tree is a complete binary tree.

Your job is to first insert a given sequence of integers into an initially empty max-heap, then to judge if a given description of the resulting heap structure is correct or not. There are 5 different kinds of description statements:

• x is the root
• x and y are siblings
• x is the parent of y
• x is the left child of y
• x is the right child of y

Input Specification:

Each input file contains one test case. For each case, the first line gives 2 positive integers: N (≤1,000), the number of keys to be inserted, and M (≤20), the number of statements to be judged. Then the next line contains N distinct integer keys in [−10⁴,10⁴] which are supposed to be inserted into an initially empty max-heap. Finally there are M lines of statements, each occupies a line.

Output Specification:

For each statement, print 1 if it is true, or 0 if not. All the answers must be print in one line, without any space.

Sample Input:

5 6
23 46 26 35 88
35 is the root
46 and 26 are siblings
88 is the parent of 46
35 is the left child of 26
35 is the right child of 46
-1 is the root

Sample Output:

011010

解析：

从空树开始一个一个添加结点，每添加一个就将整棵树调整至大根堆（而不能对整个序列进行建堆的操作）。然后用sscanf判断是哪种情形。由于大根堆本来就是完全二叉树，因此根、父亲、左右孩子的下标都很容易求，剩下的就是体力活了。

#include <vector>
#include <unordered_map>
#include <iostream>

using namespace std;

int n, m;
vector<int> tree;

// 调整
void adjust (int index) {
    int i = index / 2;
    while (i >= 1 && tree[i] < tree[index]) {
        swap(tree[i], tree[index]);
        index = i; i /= 2;
    }
}

void test () {
    int i;
    scanf("%d %d", &n, &m);
    tree.resize(n + 1);
    for (i = 1; i <= n; i++) {
        scanf("%d", &tree[i]);
        adjust(i);
    }
    unordered_map<int, int> map;  // 建立从结点数值到下标的映射
    for (i = 1; i <= n; i++) {
        map[tree[i]] = i;
    }
    string s;
    getchar();
    for (i = 0; i < m; i++) {
        getline(cin, s);
        int t1, t2;
        if (s.back() == 't') {
            t1 = stoi(s.substr(0, s.find('i') - 1));
            if (t1 == tree[1]) printf("1"); else printf("0");
        } else if (s.back() == 's') {
            sscanf(s.c_str(), "%d and %d are siblings", &t1, &t2);
            if (map[t1] / 2 == map[t2] / 2 ) printf("1"); else printf("0");
        } else if (s.find("parent") < s.length()) {
            sscanf(s.c_str(), "%d is the parent of %d", &t1, &t2);
            if (map[t1] == map[t2] / 2) printf("1"); else printf("0");
        } else if (s.find("left") < s.length()) {
            sscanf(s.c_str(), "%d is the left child of %d", &t1, &t2);
            if (map[t2] * 2 == map[t1]) printf("1"); else printf("0");
        } else {
            sscanf(s.c_str(), "%d is the right child of %d", &t1, &t2);
            if (map[t2] * 2 + 1 == map[t1]) printf("1"); else printf("0");
        }
    }
}

int main () {
    test();
    return 0;
}

7-4 Recycling of Shared Bicycles (30 分)

时间限制：200 ms 内存限制：64 MB

There are many spots for parking the shared bicycles in Hangzhou. When some of the bicycles are broken, the management center will receive a message for sending a truck to collect them. Now given the map of city, you are supposed to program the collecting route for the truck. The strategy is a simple greedy method: the truck will always move to the nearest spot to collect the broken bicycles. If there are more than one nearest spot, take the one with the smallest index.

Input Specification:

Each input file contains one test case. For each case, the first line contains two positive integers: N (≤ 200), the number of spots (hence the spots are numbered from 1 to N, and the management center is always numbered 0), and M, the number of streets connecting those spots. Then M lines follow, describing the streets in the format:

S1 S2 Dist

where S1 and S2 are the spots at the two ends of a street, and Dist is the distance between them, which is a positive integer no more than 1000. It is guaranteed that each street is given once and S1 is never the same as S2.

Output Specification:

For each case, first print in a line the sequence of spots in the visiting order, starting from 0. If it is impossible to collect all the broken bicycles, output in the second line those spots that cannot be visited, in ascending order of their indices. Or if the job can be done perfectly, print in the second line the total moving distance of the truck.

All the numbers in a line must be separated by 1 space, and there must be no extra space at the beginning or the end of the line.

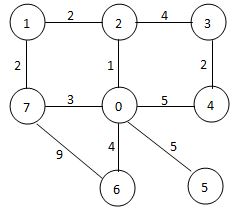
Sample Input 1 (shown by the figure below):

7 10
0 2 1
0 4 5
0 7 3
0 6 4
0 5 5
1 2 2
1 7 2
2 3 4
3 4 2
6 7 9

Sample Output 1:

0 2 1 7 6 3 4 5
33

Sample Input 2:

7 8
0 2 1
0 4 5
0 7 3
1 2 2
1 7 2
2 3 4
3 4 2
6 5 1

Sample Output 2:

0 2 1 7 3 4
5 6

解析：

题目大意：给定一张无向图和一个起点0，从起点开始，每次前往下一个最近的且没有访问过的点（允许中途路过曾经访问的点），求这些距离之和。如果按照这样的策略无法到达每个点，就把那些到不了的点打印出来。

样例1：从0开始，最近的点为2。从2开始，最近的未访问点为1。……这样顺序为0→2→1→7→6，从6开始，最近的未访问点有3、4、5，前往最小的3。以此类推，最后总路程为35。

样例2：

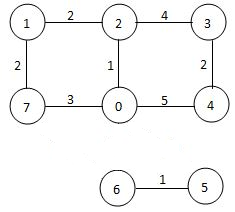
如图所示，显然6和5到不了。

方法一：多次使用迪杰斯特拉算法。可以用一个set维护所有还未访问的点。

#include <vector>
#include <algorithm>
#include <set>
#include <iostream>

using namespace std;

const int INF = 0x3fffffff, maxn = 202;

typedef struct Node {
    int to, dis;
    Node (int t, int d) : to(t), dis(d) {}
} Node;

int N, M;
int dist[maxn], visited[maxn];
vector<Node> G[maxn];

void dij (int start) {
    int i, j;
    fill(visited, visited + maxn, 0);
    fill(dist, dist + maxn, INF);
    dist[start] = 0;
    for (i = 0; i <= N; i++) {
        int cur = -1, min_dist = INF;
        for (j = 0; j <= N; j++)
            if (!visited[j] && dist[j] < min_dist) cur = j, min_dist = dist[j];
        if (cur == -1) return;
        visited[cur] = 1;
        for (auto& item : G[cur]) {
            if (visited[item.to]) continue;
            if (dist[cur] + item.dis < dist[item.to]) {
                dist[item.to] = dist[cur] + item.dis;
            }
        }
    }
}

void test () {
    int i, t1, t2, t3;
    scanf("%d %d", &N, &M);
    for (i = 0; i < M; i++) {
        scanf("%d %d %d", &t1, &t2, &t3);
        G[t1].push_back(Node(t2, t3));
        G[t2].push_back(Node(t1, t3));
    }
    set<int> to_visit;  // 所有待访问的点
    for (i = 1; i <= N; i++) to_visit.insert(i);
    int sum = 0, start = 0;
    printf("0");
    while (!to_visit.empty()) {
        dij(start);
        int min_d = INF, index = -1;
        // 在未访问点中找到最近的点
        for (auto item : to_visit) {
            if (dist[item] < min_d) min_d = dist[item], index = item;
        }
        if (index == -1) break;
        printf(" %d", index);
        sum += min_d;
        to_visit.erase(index);
        start = index;
    }
    printf("
");
    if (to_visit.empty()) {
        printf("%d", sum);
    } else {
        i = 0;
        for (auto item : to_visit) {
            printf("%d", item);
            if (i < to_visit.size() - 1) printf(" ");
            i++;
        }
    }
}

int main () {
    test();
    return 0;
}

方法二：要求所有点之间的最短距离，用弗洛伊德算法。

#include <vector>
#include <algorithm>
#include <iostream>

using namespace std;

const int INF = 0x3fffffff, maxn = 202;

int N, M, G[maxn][maxn];
int visited[maxn];

void floyd () {
    for (int k = 0; k <= N; k++) {
        for (int i = 0; i <= N; i++) {
            for (int j = 0; j <= N; j++) {
                G[i][j] = min(G[i][j], G[i][k] + G[k][j]);
            }
        }
    }
}

void test () {
    int i, j, t1, t2, t3;
    scanf("%d %d", &N, &M);
    fill(G[0], G[0] + maxn * maxn, INF);
    for (i = 0; i < M; i++) {
        scanf("%d %d %d", &t1, &t2, &t3);
        G[t1][t2] = G[t2][t1] = t3;
    }
    floyd();
    printf("0");
    int sum = 0, start = 0;
    visited[0] = 1;
    for (i = 0; i < N; i++) {
        // 每次前往下一个最近的且没有访问过的点
        int min_index = -1, min_dist = INF;
        for (j = 0; j <= N; j++) {
            if (visited[j] == 0 && G[start][j] < min_dist) {
                min_dist = G[start][j];
                min_index = j;
            }
        }
        if (min_index == -1) {
            break;
        }
        printf(" %d", min_index);
        sum += min_dist;
        visited[min_index] = 1;
        start = min_index;
    }
    printf("
");
    if (i == N) printf("%d", sum);
    else {
        for (i = 0, j = 0; j <= N; j++) {
            if (visited[j] == 0) {
                if (i > 0) printf(" ");
                printf("%d", j);
                i++;
            }
        }
    }
}

int main () {
    test();
    return 0;
}

总结

编号	标题	分数	类型
7-1	Arithmetic Progression of Primes	20	5.4 素数
7-2	Lab Access Scheduling	25	4.4 贪心
7-3	Structure of Max-Heap	25	9.7 堆
7-4	Recycling of Shared Bicycles	30	10.4 最短路径

20和19年的甲级春在当年的三次考试中是比较简单的，21年甲级春似乎要继续沿袭这个风格了（？）。就考点而言，数学问题、算法思想、树、图都有涉及，考察得还是蛮广泛的。就考察频率而言，值得注意的是，如果我没有记错，区间贪心应该是甲级第一次考察。第四题也是，至少对我而言，看到最短路径下意识就是迪杰斯特拉算法，但这题用弗洛伊德的的确确更简洁一点。总地来说学习还是得全面，不能光做老题。也许下一次负权图或者关键路径就出现了呢。。。