上午篇
一、高精度计算;
【以下内容先只考虑非负数情况】
•高精度加法:
思路:【模拟竖式运算】
注意:【进位】
•高精度减法:
思路:【同加法类似,模拟竖式运算,进位变退位】
注意: 【结果为负数的情况(一会儿讲到)】
•高精度乘法:
思路:【类似,模拟竖式运算,考虑进位】
注意:【结果为0的情况】
附总代码:
#include<iostream> #include<algorithm> #include<cstdio> #include<cmath> #include<cstring> #include<cstdlib> using namespace std; char str[1000]; int a[1000],b[1000],c[1000]; int main(){ scanf("%s", str); int len=strlen(str); // '36' for(int i=len-1;i>=0;i--)a[len-i]=str[i]-'0'; // scanf("%s", str); int n=len; /*len=strlen(str); // '36' for(int i=len-1;i>=0;i--)b[len-i]=str[i]-'0'; int m=len;//将数字转成字符串输入 n=max(n,m);*/ //for(int i=1;i<=n;i++)c[i]=a[i]...b[i];//...处为运算符号 /*for(int i=1;i<=n;i++){ c[i+1]+=c[i]/10; c[i]%=10;//模拟进位,以下被注释掉的大多也一样; }*/-----高精加法部分 /*for(int i=1;i<=n;i++) if(c[i]<0){ c[i]+=10; c[i+1]-=1; } while(c[n]==0)n-=1;*/-----高精减法部分 /*for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) c[i+j-1] += a[i]*b[j]; for(int i=1;i<=n+m-1;i++){ c[i+1]+=c[i]/10; c[i]%=10; } n=n+m-1; while(c[n+1]>0)n+=1;*/-----高精乘法部分 /*int B; cin>>B; cout<<B<<endl; for(int i=n;i>0;i--){ c[i]=a[i]/B; a[i-1]+=(a[i]%B)*10; } while(c[n]==0 && n>0)n--;*/-----高精除以低精部分 for(int i=n;i>0;i--)printf("%d",c[i]); }
•那么,负数怎么办呢?
其实可以分三种
(1)加法:
一个数是负数:变为减法;
两个数是负数:全部变成正数算加法,最后取负;
(2)减法:
被减数是负数:全部变为正整数算加法,最后取负
减数是负数:减数取负,变为加法
都是负数:都取负,变为减法,即(-减数)-(-被减数)
(3)乘除法:
统计负数个数s
都变为非负数计算,若s为奇数,最后取负
二、模意义下运算
•以七为例,模7意义下的运算:
(1)加法: 4 + 5 = 2 (4 + 5 = 9 = 7 * 1 + 2)
(2)减法: 4 - 5 = 6 (4 - 5 = - 1 = 7 * 1 - 6)
(3)乘法: 3 * 3 = 2 (3 * 3 = 9 = 1 * 7 + 2)
(4)除法: 3 / 3 = 1 (3 / 3 = 1 = 0 * 7 + 1)
(5)良心发现: 模意义下没有除法 ---蛤蛤蛤---
•模意义下运算的性质:
(1)满足基本的交换律、分配律、结合律
(2)对中间结果取模不影响最终答案
例:5 * 5 * 5 mod 7
=(5 * 5 mod 7)* 5 mod 7
= 4 * 5 mod 7
= 20 mod 7
= 6
• 快速幂:
题目描述:计算a ^ b % p = ?
三种思路:
(1)暴力(不说了,太难)
(2)分治

(3)神奇的快速幂(当做模板来记得了)
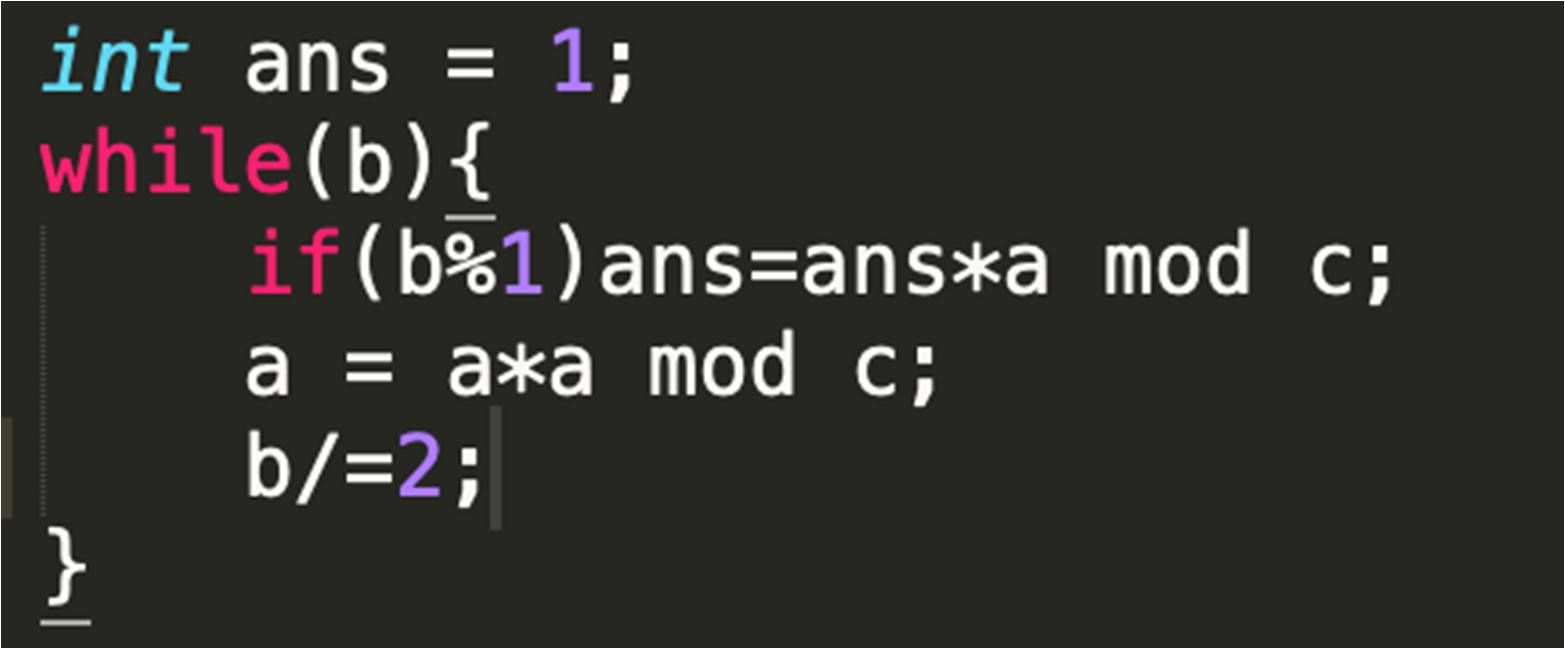
•费马小定理:
(1)定义:
对于素数p和任意正整数a(0~p-1),有a ^ (p-1) ≡ 1(mod p)
(2)应用:
计算C(n,m) % 10^ + 7
解:
C ( n , m ) = n ! / ( ( n - m ) ! * m ! )
= n ! * ( ( n - m ) ! * m ! ) ^ ( p - 2 )
= n ! * ( ( n - m ) ! ) ^ ( p - 2 ) * ( m ! ) ^ ( p - 2 )
•最大公约数
(1)一个叫gcd的东西
(2)gcd ( a , b ) = gcd ( b , a mod b )
(3)

•最小公倍数
(1)一个叫李春梅lcm的东西
(2)lcm ( a , b ) = a * b / gcd ( a, b )
(3)

•质数判别
(1)sqrt判别

(2)诶式筛
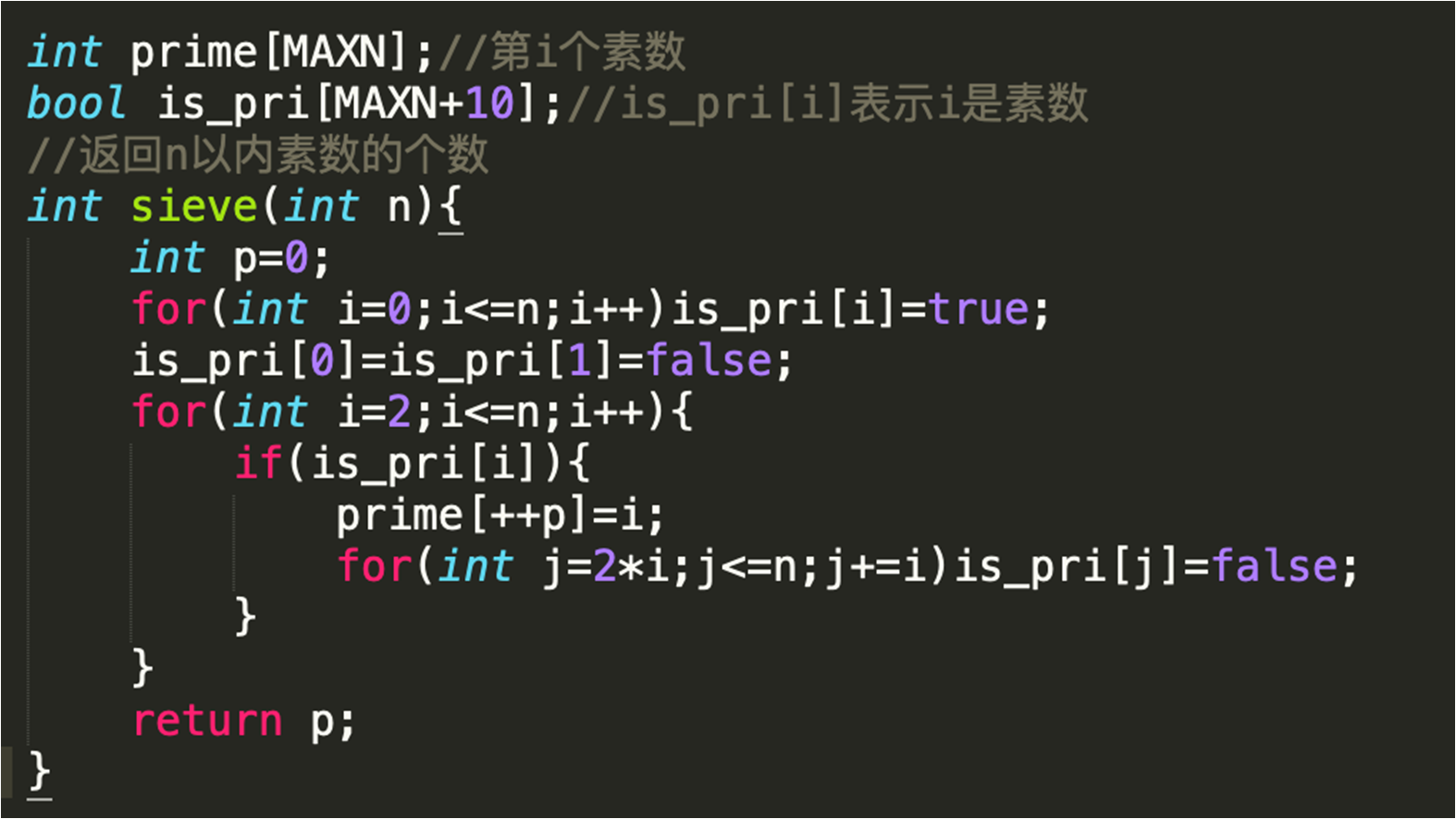
(3)线性筛

•欧拉函数
见选修4-6
下午篇
•蒟矩阵乘法
(1)一个m * n的矩阵就是m * n个数排列成m行n列的一个【数阵】
(2)一个m * p的矩阵A乘以一个p * n的矩阵B得到一个m * n的矩阵
(3)其中
(AB)ij=∑(k=1,p)aikbkj;
(4)图片描述
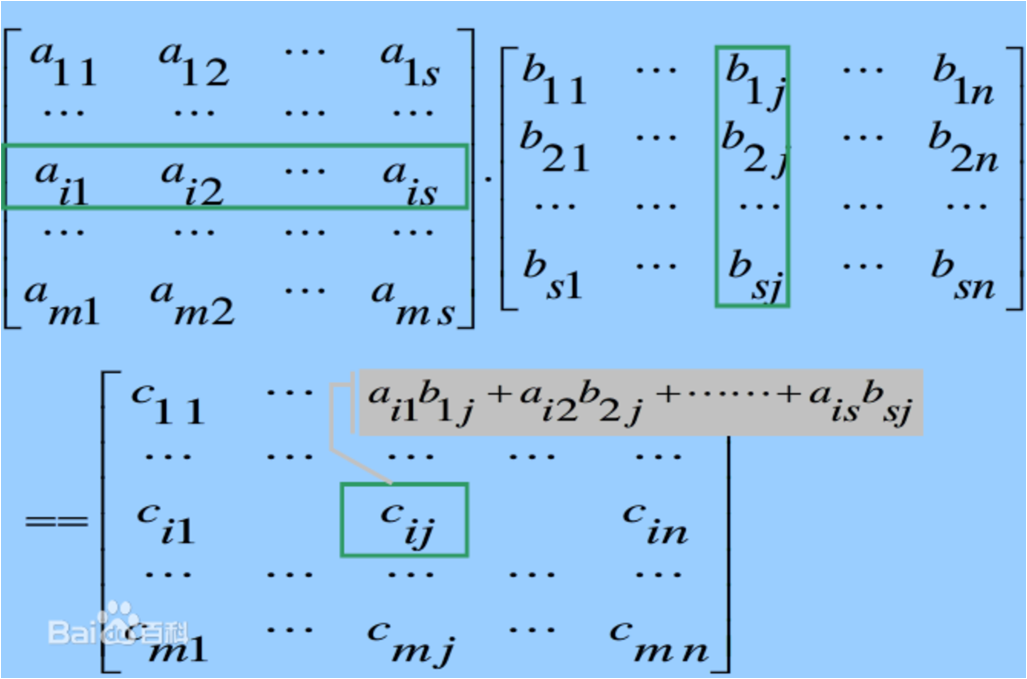
(5)例题
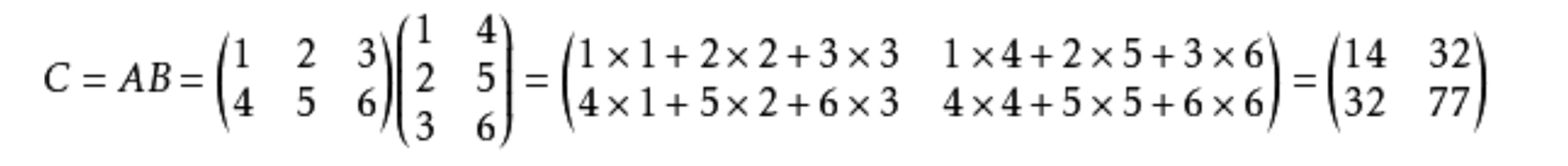
(6)注意: 矩阵乘法满足结合律、分配律,不满足交换律
(7)特殊矩阵的矩阵乘法:
上三角矩阵
分块矩阵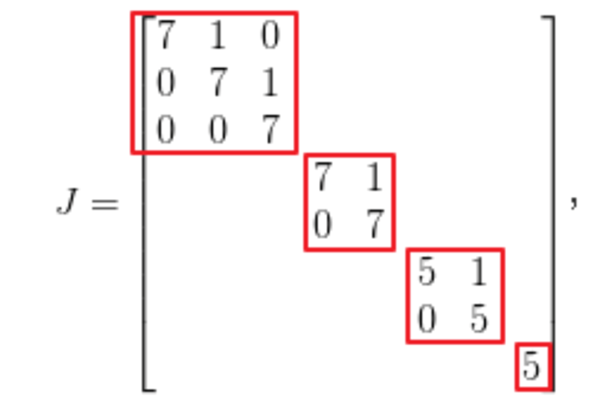
对角矩阵
对称矩阵
•行列式
(1)定义
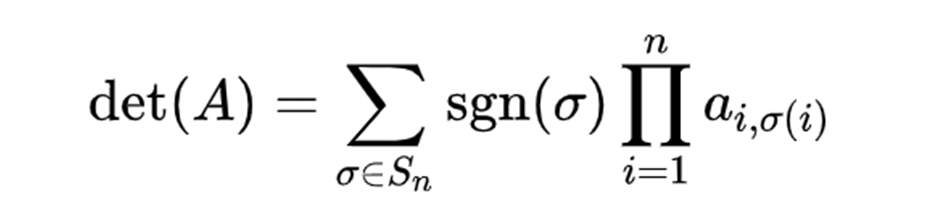
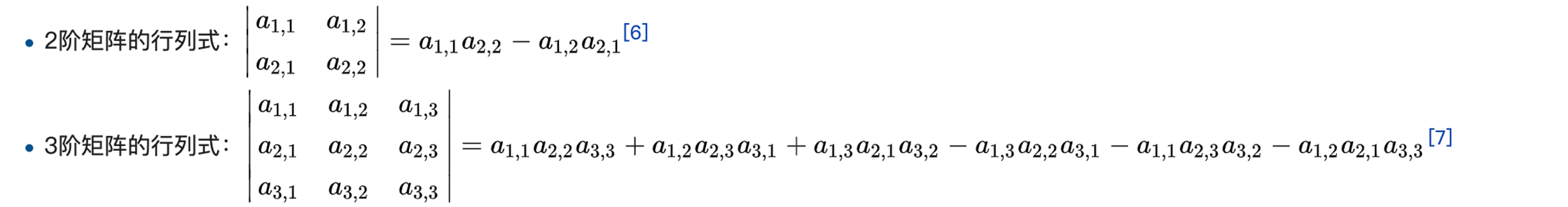
哈哈其实是计算啦
(2)计算

•矩阵树定理
•有向图—矩阵树定理

***谢谢大家***