[整理]NOIP 2020题解

前言

NOIP 爆零的作者直到现在才想起应该写点东西。
洛谷题目编号 P7113-P7116 。

T1 排水系统

0.Description

有一个(n)个点构成的 DAG ，前(m)个点有(1)的流量，每个点会将接收到的所有流量平分给所连接的出点。问最终所有没有出点的点的流量。

1.Solution

在拓扑排序的过程中计算就行了。
注意分母可能达到(60^{11})，需要高精度。
代码比较简单就不放了。

2.Summary

考试时一定要心思缜密，仔细读题，注意数据范围。

T2 字符串匹配

0.Description

定义(F(S))为字符串(S)中出现奇数次的字符数量，求将给定字符串(S)划分成((AB)^iC)（其中(F(A)le F(C))）形式的方案数。

1.Solution

把题目转化一下，变成枚举一个字符串(AB)，判断((AB)^i)是不是(S)的前缀。
那么首先我们需要解决的问题是如何判断一个字符串是否为((AB)^i)的形式。相信大家都学过 Hash 求最小周期，但是经实测直接把板子套上会出问题，那么我们来考虑另一种方式： KMP 。
KMP 的一个应用就是求最小周期，关于式子(T=|S|-next[|S|])的证明网上有不少，这里不再赘述。此时要注意特判循环次数防止原串不循环。
关于题目中的(F(S))，它非常烦人，考虑预处理出来。由于用到(F)函数的(A)和(C)分别是前缀和后缀，所以我们可以(mathcal{O(n)})预处理出每个前/后缀中出现次数为奇数的字符数量。
然后观察题目中(F(A)le F(C))的条件，我们可以想到，当(C)固定时，求出现奇数次的字符(le F(C))的(A)的数量，这个可以在计算答案时一并求出。
具体地说，设pre,suf为前/后缀出现次数为奇数的字符数量，res为出现奇数次的字符(le F(C))的(A)的数量，那么对于一个(A)和(C)，它们对答案的贡献就是res[suf[i+1]]（其中i是字符串(AB)的结尾）。

2.Code

这个复杂度常数较大，很容易被卡，需要注意一下。

const int N=1048600;
int T,n,pre[N],suf[N],res[27];
LL ans;
char s[N];
int nxt[N];
il void KMP(){
  memset(nxt,0,sizeof(nxt));
  int j;
  for(rg int i=2;i<=n;i++){
    j=nxt[i-1];
    while(s[i]!=s[j+1]&&j)j=nxt[j];
    if(s[i]==s[j+1])nxt[i]=j+1;
  }
}
il void InitPreSuf(){
  memset(pre,0,sizeof(pre));
  memset(suf,0,sizeof(suf));
  int cnt[27];
  for(rg int i=1;i<=26;i++)cnt[i]=0;
  for(rg int i=1;i<=n;i++){
    cnt[s[i]-96]++;
    if(cnt[s[i]-96]&1)pre[i]=pre[i-1]+1;
    else pre[i]=pre[i-1]-1;
  }
  for(rg int i=1;i<=26;i++)cnt[i]=0;
  for(rg int i=n;i>=1;i--){
    cnt[s[i]-96]++;
    if(cnt[s[i]-96]&1)suf[i]=suf[i+1]+1;
    else suf[i]=suf[i+1]-1;
  }
}
il void Init(){
  ans=0;
  scanf("%s",s+1),n=strlen(s+1);
  InitPreSuf(),KMP();
  memset(res,0,sizeof(res));
}
signed main(){
  Read(T);
  while(T--){
    Init();
    for(rg int i=1;i<n;i++){
      if(i>1){
        ans+=res[suf[i+1]];
        for(rg int j=i+i;j<n;j+=i){
          int len=j-nxt[j];
          if((i%len==0)&&(j/len>1))ans+=res[suf[j+1]];
          else break;
        }
      }
      for(rg int j=pre[i];j<=26;j++)res[j]++;
    }
    cout<<ans<<endl;
  }
  return 0;
}

3.Summary

不要被奇怪的题面吓到，尝试一步步分析；及时复习不熟的算法，你永远不知道(mathfrak{CCF})下次会考什么。

T3 移球游戏

0.Description

有(n+1)根柱子和(m)种颜色的球，一开始所有球被平均分到前(n)根柱子上。现在你可以移动这些球，每次移动只能从一根柱子的顶端将一个球放到另一根柱子顶端。请你构造一种方案，使得移动结束后前(n)根柱子每一根只有一种颜色（也就是(m)个同色的球），且移动次数不超过(820000)。

1.Solution

对于这样的构造题，正解一般不唯一，所以建议先自己思考方案，我的题解也仅供参考。

如果你实在没有头绪，那么请往下翻。
先考虑一个简单的情况：如果只有两种颜色，怎么办？

如图所示，
1.统计出柱1有s个1，从柱2取s个到柱n+1；
2.将柱1中的0和1分配到柱2和柱n+1（此时柱2有s个连续1，柱n+1有m-s个连续0）；
3.柱2取s个到柱1，柱n+1取m-s个到柱1，柱2取m-s个到柱n+1，柱1取m-s个到柱2；（此时柱1只有s个1，柱2只有m-s个0）
4.将柱n+1中的0和1分配到柱1和柱2（此时柱1全为1，柱2全为0）。
这样，我们就利用一根空柱，完成了对两根柱子的“整理”（建议停下来几分钟，模拟一下这个过程就会发现它的妙处）。
现在，考虑如何将原问题转化为简化问题。
而我们的做法就是：二分，(le mid)的为0，(>mid)的为1。这里有一道题可以帮助理解这种策略：洛谷P2824 [HEOI2016/TJOI2016]排序。
二分后，对于(mid)两边的任意两根未整理的柱子，我们可以用相同的策略将其整理出一根全0或一根全1。以下以构造全0列为例：

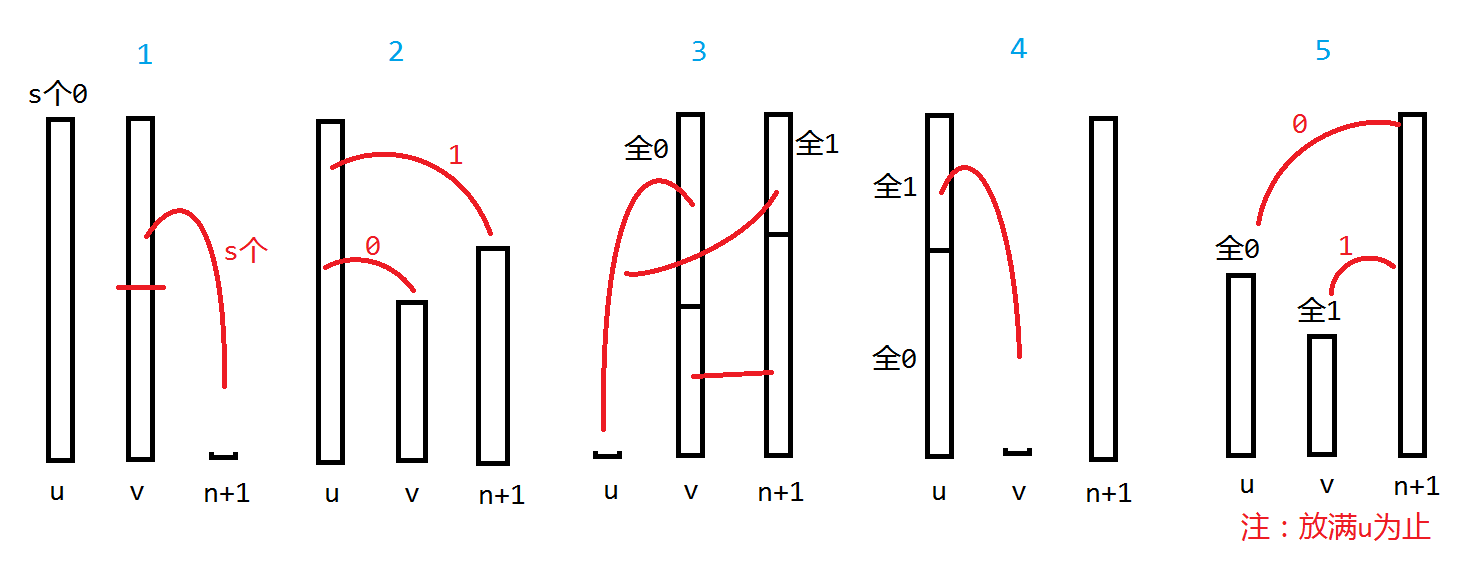
这样，这道题就做完了（步数懒得写了你们自己算去吧）。

2.Code

#define N 55
#define M 410
int n,m,tot,ans[2][820010],ok[N];
int st[N][M],tp[N];
il void Move(int x,int y){
  ans[0][++tot]=x,ans[1][tot]=y;
  st[y][++tp[y]]=st[x][tp[x]--];
}
void Solve(int l,int r){
  if(l==r)return;
  int mid=nmid;
  memset(ok,0,sizeof(ok));
  for(rg int u=l;u<=mid;u++){
    for(rg int v=mid+1;v<=r;v++){//选择两个乱序的 
      if(ok[u]||ok[v])continue;
      int s=0;//统计1的数量 
      for(rg int i=1;i<=m;i++)s+=(st[u][i]>mid);
      for(rg int i=1;i<=m;i++)s+=(st[v][i]>mid);
      if(s<m){//把u变成全0 
        s=0;
        for(rg int i=1;i<=m;i++)s+=(st[u][i]<=mid);
        for(rg int i=1;i<=s;i++)Move(v,n+1);
        while(tp[u]){
          if(st[u][tp[u]]<=mid)Move(u,v);
          else Move(u,n+1);
        }
        for(rg int i=1;i<=s;i++)Move(v,u);
        for(rg int i=1;i<=m-s;i++)Move(n+1,u);
        for(rg int i=1;i<=m-s;i++)Move(v,n+1);
        for(rg int i=1;i<=m-s;i++)Move(u,v);
        while(tp[n+1]){
          if(tp[u]<m&&st[n+1][tp[n+1]]<=mid)Move(n+1,u);
          else Move(n+1,v);
        }
        ok[u]=1;
      }else {//把v变成全1 
        s=0;
        for(rg int i=1;i<=m;i++)s+=(st[v][i]>mid);
        for(rg int i=1;i<=s;i++)Move(u,n+1);
        while(tp[v]){
          if(st[v][tp[v]]>mid)Move(v,u);
          else Move(v,n+1);
        }
        for(rg int i=1;i<=s;i++)Move(u,v);
        for(rg int i=1;i<=m-s;i++)Move(n+1,v);
        for(rg int i=1;i<=m-s;i++)Move(u,n+1);
        for(rg int i=1;i<=m-s;i++)Move(v,u);
        while(tp[n+1]){
          if(tp[v]<m&&st[n+1][tp[n+1]]>mid)Move(n+1,v);
          else Move(n+1,u);
        }
        ok[v]=1;
      }
    }
  }
  Solve(l,mid),Solve(mid+1,r);
}
int main(){
  Read(n),Read(m);
  for(rg int i=1;i<=n;i++){
    for(rg int j=1,x;j<=m;j++){
      Read(x),st[i][++tp[i]]=x;
    }
  }
  Solve(1,n),cout<<tot<<endl;
  for(rg int i=1;i<=tot;i++)cout<<ans[0][i]<<" "<<ans[1][i]<<endl;
  return 0;
}

3.Summary

对于构造题要加强练习，否则会无从下手；考试时一定要多抠抠样例（虽然这个程序跑出来不是样例），说不定就能抠出来。

T4 微信步数

0.Description

题面太恶心去洛谷看原题吧orz

1.Solution

以下的推导过程参照了其他人的题解并且省略了部分证明，如有疏忽还请指出。
这道题十分难以下手，很多人可能看到高维空间就炸了（比如我）。那么我们不妨换一种角度，从一个一个点看变为计算每一步的贡献。
如果我们能求出每一步有多少个点走出场地，不就可以很容易地求出答案了吗？
发现每次出局的点一定是边上一圈，于是我们设(l_i,r_i)表示维度(i)上存活点坐标的最值。
接下来我们会得出一些奇奇怪怪的结论，如果不好理解就放到三维空间里模拟一下。
结论一：走了一圈后的位移向量(vec{v}=vec{0})且有一点存活(Leftrightarrow)无解。
结论二：若第(i)步产生贡献，则贡献值为(iprod_{j e c_i}(r_j-l_j+1))。
接下来，我们会利用步数的周期性瞎猜得出一些性质。
设([k,i])表示第(k)轮第(i)步对答案做出贡献，则：
结论三：([1,i] Rightarrow[2,i],[1,i]&[2,i]Rightarrow [k,i](k>2))
此结论易证，故略去证明。不知道怎么证就扔给读者的屑
我们还有一个结论，就是如果一个第(i)步的点存活到了第(i+n)步，我们发现它正好走过了一个位移向量（我们用(v_j)表示位移向量的第(j)维），相应的(l_j)和(r_j)也会发生变化：
结论四：(i ightarrow i+n, r_j-l_j+1 ightarrow r_j-l_j+1-|v_j|)
对此，我们可以推出另一个结论：
结论五：若([2,i])且([x,i](x>2))，则第(x)轮第(i)步造成的贡献为((nx+i)prod_{j e c_i}[r_j-l_j+1-|v_j|(x-1)])
所以我们发现此时已经可以求出答案。具体地说，先特殊计算出第一轮的，再计算第二轮的，计算第二轮的同时枚举(x)。
时间复杂度大概是一个非常宽松的(mathcal{O(nkw)})，可以水过80分。

这个算法的瓶颈在于(w)，我们考虑优化掉它。
观察上面的式子，对于每个(i)我们用(f(x))来表示((nx+i)prod_{j e c_i}[r_j-l_j+1-|v_j|(x-1)])，接下来探讨一下关于(f)的性质。
容易发现，(f)是一个(k)次多项式，我们可以暴力把后面的乘出来，假设乘积(f(x)=sum_{i=0}^k a_ix^i)。
假设我们需要算(cnt)轮，那么所有(i+nx)的贡献就是(sum_{x=1}^{cnt}f(x)=sum_{x=1}^{cnt}sum_{i=0}^k a_ix^i)。（废话）
易知其中(cnt=min_{1le jle k,v_j e0}left{dfrac{r_j-l_j}{v_j}+1 ight})。
我们交换一下枚举顺序，原式变为(sum_{i=0}^k(a_isum_{x=1}^{cnt}x^i))。通过观察不难得出，我们需要解决的是里面(sum_{x=1}^{cnt}x^i)这一部分，
而这一部分的求法可以参照CF622F The Sum of the k-th Powers。
于是，我们解决了这道题，时间复杂度为(mathcal{O(nk^2)})。代码里细节比较多，需要注意一下。

2.Code

const int N=500010,K=15,mod=1000000007;
int n,k,w[K],c[N],d[N],v[K],u[K],l[K],r[K],ans;
struct Poly {
  int sz,num[K];
  Poly(){
    sz=0,memset(num,0,sizeof(num));
  }
  Poly(int _sz,int _C,int _X){
    sz=_sz,num[0]=_C,num[1]=_X;
  }
};
il Poly operator + (Poly a,Poly b){
  Poly c;c.sz=max(a.sz,b.sz);
  for(rg int i=0;i<=c.sz;i++){
    c.num[i]=(a.num[i]+b.num[i])%mod;
  }
  return c;
}
il Poly operator * (Poly a,Poly b){
  Poly c;c.sz=a.sz+b.sz;
  for(rg int i=0;i<=a.sz;i++){
    for(rg int j=0;j<=b.sz;j++){
      c.num[i+j]=(c.num[i+j]+a.num[i]*b.num[j]%mod)%mod;
    }
  }
  return c;
}
il int Pow(int a,int b,int p){
  int res=1;
  while(b){
    if(b&1)res=res*a%p;
    a=a*a%p,b>>=1;
  }
  return res;
}
int fac[N];
il int Calc(int n,int m){//sum_{k=1}^n k^m
  int res=0;
  if(n<=m+2){
    for(rg int i=1;i<=n;i++){
      res=(res+Pow(i,m,mod))%mod;
    }
    return res;
  }
  fac[0]=1;
  for(rg int i=1;i<=m+1;i++)fac[i]=fac[i-1]*i%mod;
  int all=1,sk=0,ff=(m+2)&1?1:-1;
  for(rg int i=1;i<=m+2;i++)all=all*(n-i)%mod;
  for(rg int i=1;i<=m+2;i++,ff=-ff){
    sk=(sk+Pow(i,m,mod))%mod;
    int p=all*Pow(n-i,mod-2,mod)%mod;
    int q=fac[i-1]*fac[m+2-i]%mod*ff;
    res=(res+sk*p%mod*Pow(q,mod-2,mod)%mod)%mod;
  }
  return (res+mod)%mod;
}
signed main(){
  Read(n),Read(k);
  for(rg int i=1;i<=k;i++)Read(w[i]),l[i]=1,r[i]=w[i];
  for(rg int i=1;i<=n;i++)Read(c[i]),Read(d[i]);
  for(rg int i=1;i<=n;i++){
    int cc=c[i];
    v[cc]+=d[i];
    if(v[cc]>0){
      int dlt=v[cc];
      if(w[cc]-dlt<r[cc])r[cc]=w[cc]-dlt;
    }else if(v[cc]<0){
      int dlt=-v[cc];
      if(dlt+1>l[cc])l[cc]=dlt+1;
    }
  }
  for(rg int i=1;i<=k;i++){//判定是否满足无解的两个条件 
    if(l[i]>r[i]||v[i])goto OK;
  }
  puts("-1");
  return 0;
  OK:
  for(rg int i=1;i<=k;i++)l[i]=1,r[i]=w[i];
  for(rg int i=1;i<=n;i++){//模拟第一轮 
    int cc=c[i];
    u[cc]+=d[i];
    bool mv=0;
    if(u[cc]>0){
      int dlt=u[cc];
      if(w[cc]-dlt<r[cc])r[cc]=w[cc]-dlt,mv=1;
    }else if(u[cc]<0){
      int dlt=-u[cc];
      if(dlt+1>l[cc])l[cc]=dlt+1,mv=1;
    }
    if(mv){
      int prod=1;
      for(rg int j=1;j<=k;j++){
        if(j==cc)continue;
        prod=prod*(r[j]-l[j]+1)%mod;
      }
      ans=(ans+prod*i%mod)%mod;
      if(l[cc]>r[cc]){
        cout<<ans<<endl;
        return 0;
      }
    }
  }
  for(rg int i=n+1;i<=n+n;i++){//模拟第二轮及以后 
    int cc=c[i-n];
    u[cc]+=d[i-n];
    bool mv=0;
    if(u[cc]>0){
      int dlt=u[cc];
      if(w[cc]-dlt<r[cc])mv=1;
    }else if(u[cc]<0){
      int dlt=-u[cc];
      if(dlt+1>l[cc])mv=1;
    }
    if(mv){
      int cnt=INF;
      for(rg int j=1;j<=k;j++){
        if(!v[j])continue;
        cnt=min(cnt,(r[j]-l[j])/abs(v[j])+1);
      }
      Poly f=Poly(1,i-n,n);
      for(rg int j=1;j<=k;j++){
        if(j==cc)continue;
        f=f*Poly(1,r[j]-l[j]+1+abs(v[j]),mod-abs(v[j]));
      }
      for(rg int j=0;j<=k;j++){
        ans=(ans+f.num[j]*Calc(cnt,j)%mod)%mod;
      }
    }
    if(u[cc]>0){
      int dlt=u[cc];
      if(w[cc]-dlt<r[cc])r[cc]=w[cc]-dlt;
    }else if(u[cc]<0){
      int dlt=-u[cc];
      if(dlt+1>l[cc])l[cc]=dlt+1;
    }
    if(l[cc]>r[cc]){
      cout<<ans<<endl;
      return 0;
    }
  }
  cout<<ans<<endl;
  return 0;
}

（需要开long long）

3.Summary

遇到不会的题要耐心推式子，尽量多得分；知识面一定要拓宽（话说(mathfrak{CCF})在一场比赛里考了两个奇奇怪怪的知识点了）。

完结撒花！！！