[整理]qbxt周末刷题班 Day1总结

A

Description:把一个(n imes m)的字母矩阵里的每一行每一列拿出来，有(q)次单点修改操作，问每次操作后和初始情况下本质不同的字符串个数。
Solution:一个朴素的想法是暴力加入(set)或(map)，期望得分60分。考场实测60
正解是(hash)，但是毒瘤出题人卡了单哈希所以要双哈希。
Code:有亿些复杂先咕一会

B

Description:有一棵(n)个点的树，求从任意一个点出发，只能走(a)步或(b)步且不能走之前走过的边时能到达的点数。多组数据。
几个部分分：(a)、(b)互质；(a=b)；一条链。
Solution:由于树上两点之间路径唯一，我们不难想到一个点能够走到的条件是以起点为根时的深度能被(a)和(b)表出（即(dist=ax+by)）。
但是正解不是很好想，我们先来看几个部分分。
(a=b)：可以用(f[i][j])表示(i)子树里膜(a)余(j)的点数，然后进行换根dp。
(a)、(b)互质：运用(NOIP2017 D1T1)的结论，只需要考虑深度小于(ab-a-b)的点即可。
考虑一般情况：
发现一个点能走到的必要条件是深度为(gcd(a,b))的倍数。
我们考虑统计一个(gcd(a,b))倍数的(f1)数组，求出可能走到的点的个数，然后类比(a)、(b)互质的情况，再统计一个(f2)数组，这样一减便能求出最终答案。
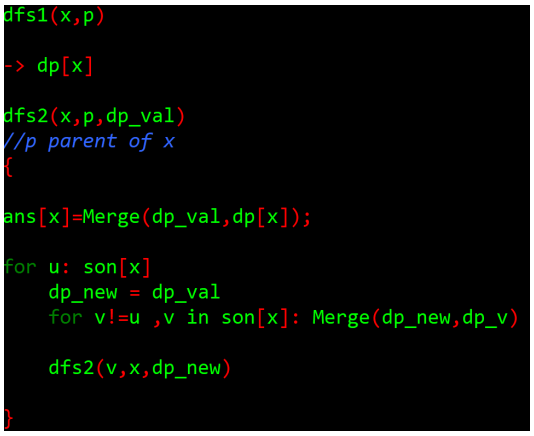
Implementation:在换根的第二个DFS里传入两个vector分别代表两组dp值，然后换根。
需要求出一个vis数组表示每个点是否可达，然后在统计时减掉。
顺便放一张老师讲的换根dp常见套路：

Code:

#define N 100010
int T,n,a,b,g,mn;
int f1[N][80],f2[N][11],ans1[N][80],ans2[N][80],vis[80];
vector<int>e[N];
inline void ade(int u,int v){
	e[u].pub(v),e[v].pub(u);
}
void DFS(int now,int ff){
	f1[now][0]=f2[now][0]=1;
	for(rg int i=0;i<e[now].size();i++){
		int v=e[now][i];
		if(v!=ff){
			DFS(v,now);
			for(rg int j=1;j<=mn;j++)f1[now][j]+=f1[v][j-1];
			for(rg int j=0;j<g;j++)f2[now][(j+1)%g]+=f2[v][j];
		}
	}
}
void DFS2(int now,int ff,vector<int>v1,vector<int>v2){
	for(rg int i=0;i<=mn;i++){
		ans1[now][i]=f1[now][i]+v1[i];
		v1[i]+=f1[now][i];
	}
	for(rg int i=0;i<g;i++){
		ans2[now][i]=f2[now][i]+v2[i];
		v2[i]+=f2[now][i];
	}
	for(rg int i=0;i<e[now].size();i++){
		int v=e[now][i];
		if(v!=ff){
			for(rg int j=0;j<mn;j++)v1[j+1]-=f1[v][j];
			for(rg int j=0;j<g;j++)v2[(j+1)%g]-=f2[v][j];
			vector<int>n1,n2;n1.resize(mn+1,0),n2.resize(g,0);
			for(rg int j=1;j<=mn;j++)n1[j]=v1[j-1];
			for(rg int j=0;j<g;j++)n2[(j+1)%g]=v2[j];
			DFS2(v,now,n1,n2);
			for(rg int j=0;j<mn;j++)v1[j+1]+=f1[v][j];
			for(rg int j=0;j<g;j++)v2[(j+1)%g]+=f2[v][j];
		}
	}
}
int main(){
	Read(T);
	while(T--){
		for(rg int i=0;i<N;i++)e[i].clear();
		memset(f1,0,sizeof(f1)),memset(f2,0,sizeof(f2)),memset(vis,0,sizeof(vis));
		Read(n),Read(a),Read(b);
		g=__gcd(a,b),mn=max(0,a/g*b/g-a/g-b/g)*g;
		for(rg int i=1;i<n;i++){
			int u,v;Read(u),Read(v),ade(u,v);
		}
		DFS(1,-1);
		vector<int>v1,v2;v1.resize(mn+1,0),v2.resize(g,0);
		DFS2(1,-1,v1,v2);
		vis[0]=1;
		for(rg int i=1;i<=mn;i++){
			if(i>=a)vis[i]|=vis[i-a];
			if(i>=b)vis[i]|=vis[i-b];
		}
		for(rg int i=1;i<=n;i++){
			int res=ans2[i][0];
			for(rg int j=0;j<=mn;j+=g){
				if(!vis[j])res-=ans1[i][j];
			}
			cout<<res<<" ";
		}
		cout<<endl;
	}
	return 0;
}

C

Description:有一个高(h)的游戏机，第(i)行有(i)个格子，每轮从第一个格子放入一个小球，小球等概率地落到下方两个格子的任意一个中。如果小球最终落到的格子中已经有球，那么游戏结束，得0分；如果小球落到空格子里，那么可以选择结束游戏得(acnt^2+bcnt)分（其中(cnt)为当前轮数），也可以选择开始新一轮游戏。问在最优策略下期望能得多少分（保留四位小数）。
Solution:对于前几种(h)较小的情况我们可以暴力枚举方案，但是最大的(h)可以达到26，这启发我们采用状压(dp)来做。
Implementation:首先用类似杨辉三角的方式算出概率，然后我们设(f[st])为最后一行状态为(st)情况下的期望得分，这时采用记搜来实现这个(dp)。
具体的搜索过程是通过枚举下一个球落进的格子来计算出继续游戏的期望得分，然后与当前得分比较后存入(f)数组。
Optimization:直接状压会爆炸，考虑如何优化状态压缩方式。
注意到概率是对称的，于是我们可以只用一半的状态来存（例如用00、01、11表示四种状态）。这样就可以完美(AC)了。
Code:

#define N 30
int T,n,a,b;
double C[N][N];
inline void Init(){
	C[1][1]=1;
	for(rg int i=2;i<N;i++){
		for(rg int j=1;j<=i;j++){
			C[i][j]=(C[i-1][j]+C[i-1][j-1])/2;
		}
	}
}
double f[70000000];
double DP(int st){
	if(f[st]>=0)return f[st];
	int cnt=__builtin_popcount(st);
	double bonus_now=a*cnt*cnt+b*cnt,bonus_con=0.0;
//	stop now / continue
	for(rg int i=1;i<=n;i++){
		if(st>>(i-1)&1)continue;//you lose the game
		int st_new=st;
		if(n-i<i&&!(st>>(n-i)&1))st_new^=1<<(n-i);
		else st_new^=1<<(i-1);
		bonus_con+=C[n][i]*DP(st_new);
	}
//	cout<<bonus_now<<" "<<bonus_con<<endl;
	return f[st]=max(bonus_now,bonus_con);
}
int main(){
	Read(T);Init();
	while(T--){
		Read(n),Read(a),Read(b);
		for(rg int i=0;i<1<<n;i++)f[i]=-1;
		printf("%.4lf
",DP(0));
	}
	return 0;
}

D

Description:

Solution:设(f[i][j])为当前在第(i)列，要从第(j)行出去的方案数。
我们可以枚举当前一行从哪一行转移来，有障碍物的不能转移。
对于(Qle 10^5)的数据，我们可以把状态转移写成矩阵，然后加一个线段树进行单点修改即可。
对于(Mle 10^9)的数据，我们可以离散化一下。
状态转移（无障碍物）：

[egin{bmatrix} 0&1&0&0\1&0&1&0\0&1&0&1\0&0&1&0 end{bmatrix} egin{bmatrix} f[i][1]\f[i][2]\f[i][3]\f[i][4] end{bmatrix} = egin{bmatrix} f[i+1][1]\f[i+1][2]\f[i+1][3]\f[i+1][4] end{bmatrix} ]

Notice:此题严重（？）卡常，我的代码需添加#pragma GCC optimize(2)才可过。
Code:

#define mod 998244353
#define Q 200010
int n,m,q,x[Q],y[Q],st[Q];
vector<int>pos;
struct Matrix {
	int r,c;
	int a[4][4];
	Matrix(int _r=0,int _c=0){
		r=_r,c=_c;
		memset(a,0,sizeof(a));
	}
};
inline Matrix Mul(Matrix A,Matrix B){
	Matrix C(A.r,B.c);
	for(rg int i=0;i<A.r;i++){
		for(rg int j=0;j<B.c;j++){
			LL tmp=0;
			for(rg int k=0;k<A.c;k++){
				tmp+=1ll*A.a[i][k]*B.a[k][j];
			}
			C.a[i][j]=tmp%mod;
		}
	}
	return C;
}
inline Matrix Pow(Matrix A,int b){
	Matrix ans(A.r,A.r);
	for(rg int i=0;i<A.r;i++)ans.a[i][i]=1;
	while(b){
		if(b&1){
			ans=Mul(ans,A);
		}
		A=Mul(A,A);
		b>>=1;
	}
	return ans;
}
Matrix tran[16],mat[Q];
struct Node {
	int l,r;
	Matrix wei;
}tr[Q<<2];
inline void Pushup(int k){
	tr[k].wei=Mul(tr[ls].wei,tr[rs].wei);
}
void Build(int k,int l,int r){
	tr[k].l=l,tr[k].r=r;
	if(l==r){
		tr[k].wei=mat[l];
		return;
	}
	int mid=nmid;
	Build(ls,l,mid);Build(rs,mid+1,r);
	Pushup(k);
}
void ModifyPoint(int k,int pos,Matrix num){
	if(Thispoint){
		tr[k].wei=num;
		return;
	}
	int mid=tmid;
	if(pos<=mid)ModifyPoint(ls,pos,num);
	else ModifyPoint(rs,pos,num);
	Pushup(k);
}
int main(){
	Read(n),Read(m),Read(q);
	for(rg int i=1;i<=q;i++){
		Read(x[i]),Read(y[i]);
		pos.pub(y[i]),pos.pub(y[i]+1);
	}
	pos.pub(1),pos.pub(m+1);
	sort(pos.begin(),pos.end());
	pos.resize(unique(pos.begin(),pos.end())-pos.begin());
	for(rg int i=0;i<(1<<n);i++){
		tran[i].r=tran[i].c=n;
		for(rg int j=0;j<n-1;j++){
			if((i>>j&1)||(i>>(j+1)&1))continue;
			tran[i].a[j][j+1]=tran[i].a[j+1][j]=1;
		}
	}
	int tot=pos.size();
	for(rg int i=0;i<tot-1;i++){
		mat[i]=Pow(tran[0],pos[i+1]-pos[i]);
	}
	Build(1,0,tot-2);
	for(rg int i=1;i<=q;i++){
		int p=lower_bound(pos.begin(),pos.end(),y[i])-pos.begin();
		st[p]|=1<<(x[i]-1);
		ModifyPoint(1,p,tran[st[p]]);
		cout<<tr[1].wei.a[0][n-1]<<endl;
	}
	return 0;
}

完结撒花