Python进阶复习
列表推导式
# 列表推导式 L = [] def my_func(x): return 2*x for i in range(5): L.append(my_func(i)) # 列表推导式[* for i in *] # 第一个 * 为映射函数,其输入为后面 i 指代的内容 # 第二个 * 表示迭代的对象。 [my_func(i) for i in range(5)]
结果为my_func(i),很巧的是,回顾这个问题,code review出同事的一个bug~
[m + '_' + n for m in ['a','b'] for n in ['c','d']]
第一个for是外循环,第二个for是内循环
习题1.3.1 列表推导式的使用
题目:

题目分析:
需要对input 141改写,item是用于累加三层循环的M1[i][k]*M2[k][j],res得到的是经过i和j两层循环后的结果,需要从里层循环到外层循环展开。里层因为得到item的累加和,是结果,故而写在列表推导式的开头,在k这层循环累加,所以是
sum([M1[i][k]*M2[k][j] for k in range(M1.shape[1])])
j层循环(2个列表推导式):
[sum([M1[i][k]*M2[k][j] for k in range(M1.shape[1])]) for j in range(M2.shape[1])]
i层循环(3个列表推导式):
[[sum([M1[i][k]*M2[k][j] for k in range(M1.shape[1])]) for j in range(M2.shape[1])] for i in range(M1.shape[0])]
放上完整代码:
import numpy as np M1 = np.random.rand(2,3) M2 = np.random.rand(3,4) # 第一个值为返回值res # 原题中item是用于累加求和,在经过i和j两层循环后,将结果存放于res res = [[sum([M1[i][k]*M2[k][j] for k in range(M1.shape[1])]) for j in range(M2.shape[1])] for i in range(M1.shape[0])] ((M1@M2 - res) < 1e-15).all()
结果: True
当结合匿名函数时
# i = 0,1,2,3,4-->i作为lambda匿名函数的自变量 # 所以lambda x: 2*x -->0,2,4,6,8 [(lambda x: 2*x)(i) for i in range(5)] # 结果:[0, 2, 4, 6, 8]
注意,利用列表推导式的匿名函数映射,返回的是一个map对象,需要通过list转为列表, map函数会根据提供的函数对指定的序列做映射,map(function,iteration),其中iteration是一个或多个序列
list(map(lambda x: 2*x, range(5)))
zip对象和enumerate方法
自己写代码时非常好用的,比如有两个list,想把其中一个list作为字典的key,另一个list作为字典value(之前需要判断两个list的长度是否一致),然后直接用zip打包即可
enumerate也是工程中非常好用的遍历方法,可以用index来debug有错误的序列,value打印对应的结果
zip是压缩的英文,那么也有对应的解压操作~

numpy
第一次认真学numpy,笔记有点多~
初始化构造array
import numpy as np # 一般都用array来构造 np.array([1,2,3])
返回的是array类型的结果:
array([1, 2, 3])
两种等差序列:(英语好的同学注意拼写,不是arrange,而是arange!)
# 等差序列,起始、终止(包含),样本个数 np.linspace(1,5,11) # array([1. , 1.4, 1.8, 2.2, 2.6, 3. , 3.4, 3.8, 4.2, 4.6, 5. ]) # 等差序列,起始、终止(不包含)、步长 np.arange(1,5,1)
# array([1, 2, 3, 4])
np.arange第三个参数是步长,故而更适合于创建规则的array,更常用
特殊矩阵,zeros, eye, full
# 类型:元组,参数为行和列的维度 np.zeros((2,3)) # array([[0., 0., 0.], # [0., 0., 0.]])
用小括号括起来的参数是维度,原本函数是np.zeros(),在()中加一个元组,第一个参数表示2行,第二个参数表示3列
# eye,3*3的单位矩阵 np.eye(3) """ array([[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]]) """
np.eye()因为是单位矩阵,只有一个参数,同时代表行和列,第二个参数是偏移主对角线1个单位的伪单位矩阵
# full,返回类型:元组 # 第一个参数为矩阵维度,第二个参数为填充的数值 np.full((2,3),10) # 返回:array([[10, 10, 10], # [10, 10, 10]]) # 第二个参数为列表,是将该传入列表填充到每行 np.full((2,3), [1,2,3]) #返回:array([[1, 2, 3], # [1, 2, 3]])
随机矩阵
# 随机矩阵 np.random # 生成服从0-1均匀分布的三个随机数 # 传入的是维度大小,3行3列 np.random.rand(3,3) array([[0.66924322, 0.21467023, 0.03326504], [0.95161185, 0.592994 , 0.77495745], [0.70362244, 0.79596363, 0.778472 ]]) # randn生成了N(0,I)的标准正态分布 # 标准正态分布,均值μ=0,标准差σ=1 # 参数是维度 np.random.randn(2,2) array([[-0.91070861, 1.91114701], [ 0.42962912, -0.59628133]]) # randint可以指定生成随机整数的最小值,最大值和维度大小 low, high, size = 5, 15, (2,2) np.random.randint(low, high, size) array([[14, 6], [ 6, 7]]) # choice可以从给定的列表中,以一定概率和方式抽取结果 # 当不指定第四个参数p概率时,为均匀采样 # 默认replace抽取方式为有放回抽样 # 出现a的概率为0.1,出现b的概率为0.7,出现c的概率0.1,出现d的概率为0.1 my_list = ['a', 'b', 'c', 'd'] np.random.choice(my_list, 2, replace=False, p=[0.1,0.7,0.1,0.1]) array(['b', 'a'], dtype='<U1')
其中,<U1的解答链接:https://segmentfault.com/q/1010000012049371

# permutation打散原列表 np.random.permutation(my_list)
array(['d', 'a', 'c', 'b'], dtype='<U1')
想到了paddlepaddle里面的shuffle参数,如果数据集因为label相同的排列太紧密,会导致模型训练效果很差,所以需要打乱数据,不知道permutation是否也有这奇效呢~
随机种子
# 随机种子,能固定随机数的输出结果 # 参数值不变时,输出的结果也不会变 np.random.seed(28) np.random.rand() # 0.7290137422891191
这个值一旦设定,在任何其他人的电脑上运行同样参数的seed函数,输出的结果都一样~
非常有用的numpy数组的变形与合并
# 常用的转置,常用于初始化,2行3列->3行2列 # 不过 reshape使用更灵活 np.zeros((2,3)).T array([[0., 0.], [0., 0.], [0., 0.]])
# 维度变换 reshape # 能帮助用户把原数组按照新的维度重新排列 # array([0, 1, 2, 3, 4, 5, 6, 7])重新按照reshape排序 print(np.arange(8).reshape(2,4)) [[0 1 2 3] [4 5 6 7]] # order为C,逐行顺序进行填充 # 对target处理顺序为0,1,2,3,4,5,6,7,逐行放置 target.reshape((4,2), order = 'C') array([[0, 1], [2, 3], [4, 5], [6, 7]]) # order为F,逐列顺序进行填充 # 对target处理顺序为0,4,1,5,2,6,3,7,以列重新排序 target.reshape((4,2), order = 'F') array([[0, 2], [4, 6], [1, 3], [5, 7]]) # 当被调用数组的大小是确定的时(2*4=8) # reshape允许有一个维度存在空缺,比如规定4行,第二个参数可设为-1 target.reshape((4, -1)) array([[0, 1], [2, 3], [4, 5], [6, 7]])
reshape的另一个妙用是,有点像.T转置是不是~但reshape用起来更方便

合并
# 上下合并 np.r_[np.zeros((2,3)), np.zeros((2,3))] array([[0., 0., 0.], [0., 0., 0.], [0., 0., 0.], [0., 0., 0.]]) # 左右合并 np.c_[np.zeros((2,3)), np.zeros((2,3))] array([[0., 0., 0., 0., 0., 0.], [0., 0., 0., 0., 0., 0.]]) # np.array([0,0])是一维数组,np.zeros(2)是二维数组 # 两者进行合并时,在长度匹配的情况下,只能使用左右合并的c_操作 np.r_[np.array([0,0]), np.zeros(2)]
常用函数
# where,条件函数,可以指定满足条件与不满足条件位置对应的填充值 a = np.array([-1,1,-1,0]) # 当为True时,填充a的值,否则填充5 # 第一个参数是判断条件,第二个参数是对应位置为True的返回结果,第三个参数是对应位置为False的返回结果 np.where(a>0, a, 5) array([5, 1, 5, 5]) # 返回索引,nonzero返回非零数的索引,argmax和argmin分别返回最大数和最小数的索引 a = np.array([-2,-5,0,1,3,-1]) np.nonzero(a) (array([0, 1, 3, 4, 5], dtype=int64),) # cumprod.cumsum 分别表示累乘和累加函数,返回同长度的数组 a = np.array([1,2,3]) # 1->1, 1*2->2, 1*2*3->6 a.cumprod() array([1, 2, 6], dtype=int32) a = np.array([1,2,3]) # 1->1, 1+2->3, 1+2+3->6 a.cumsum() array([1, 3, 6], dtype=int32) # diff表示和前一个元素做差, # 由于第一个元素为缺失值,因此在默认情况下,返回长度是原数组减1 # 数组中的差, 2-1->1, 3-2->1 np.diff(a) array([1, 1])
针对.sum()函数常用的axis参数,用了屡错屡不对
找了张经典的图:
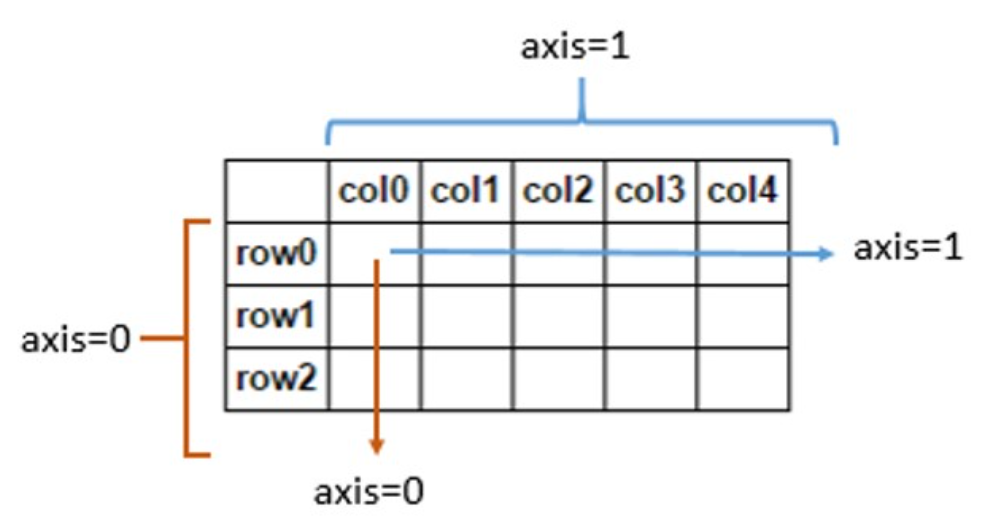
# axis参数,能进行某一个维度下的统计特征计算 target = np.arange(1,10).reshape(3,-1) target array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) # 当axis=0时,结果为列的统计指标 target.sum(0) array([12, 15, 18]) # 当axis=1时,结果为行的统计指标 target.sum(1) array([ 6, 15, 24])
针对以上知识点,例题2:

我的分析:更新方法,求每行倒数之和,然后乘以矩阵。那么,对每行倒数求和可以用
(1/a).sum(1)
结果是array([1.83333333, 0.61666667, 0.37896825])
但是,每一行的第一个值都是1.833,第二个值是0.6166,第三个值是0.3789,但是我们还要做和原先A矩阵的每一个值相乘需要将三个值在一列中排列不同变成
array([[1.83333333], [0.61666667], [0.37896825]])
(1/a).sum(1).reshape(-1,1) array([[1.83333333], [0.61666667], [0.37896825]])
# 再乘以矩阵a的每一个值 result = a*(1/a).sum(1).reshape(-1,1)
结果:
array([[1.83333333, 3.66666667, 5.5 ],
[2.46666667, 3.08333333, 3.7 ],
[2.65277778, 3.03174603, 3.41071429]])
向量和矩阵的计算
# 向量内积dot a = np.array([1,2,3]) b = np.array([1,3,5]) a.dot(b) #结果:22 # np.linalg.norm第二个参数的用法 # 向量范数和矩阵范数: np.linalg.norm # 1-范数:向量元素绝对值之和 # 2-范数:向量元素绝对值的平方和再开平方 # p-范数:向量元素绝对值的p次方和的1/p次幂 # 矩阵范数:1-范数:所有矩阵列向量绝对值之和的最大值 # 矩阵范数:2-范数:A'A矩阵的最大特征值的开平方 # 矩阵范数:Frobenius范数,矩阵元素绝对值的平方和再开平方 matrix_target = np.arange(4).reshape(-1,2) # 'fro'是Frobenius norm np.linalg.norm(matrix_target, 'fro') # 结果:3.7416573867739413 #对于matrics,max(sum(abs(x), axis=1)) # 按行,对每一行的绝对值求和 np.linalg.norm(matrix_target, np.inf) # 5.0
矩阵乘法
a = np.arange(4).reshape(-1,2) b = np.arange(-4,0).reshape(-1,2) a@b array([[ -2, -1], [-14, -9]])g b@a array([[ -6, -13], [ -2, -5]])
注意两个矩阵相乘前后顺序很重要
相关习题:

分析:主要是对B的问题,转换为用内积解决,即np.dot(),也就是对A矩阵的行(axis=1)求和,对A矩阵的列(axis=0)求和,然后相乘。最后再套公式:
A = np.random.randint(10,20,(8,5)) B = np.dot(A.sum(axis=1,keepdims=True),A.sum(axis=0,keepdims=True))/A.sum() result = (((A-B)**2)/B).sum()
一开始,没有keepdims=True,是报错的,经查后,才发现这个参数是用来保持矩阵的二维性。如果一个2*3*4的三维矩阵,axis=0,keepdims默认为False,则结果矩阵被降维至3*4(二维矩阵) 。如果keepdims=True, 则矩阵维度保持不变,还是三维,只是第零个维度由2变为1,即1*3*4的三维矩阵。有了这个选项,结果矩阵就可以与原始输入矩阵进行正确的广播运算
最后这个算法题:

我的分析:递增可以用np.diff,如果递增且是连续整数,则后一个数减去前一个数,结果一定为1,否则,可以用其他值填充。因为np.diff是会少一位,所以要在首位填充1,可以像bert模型,最,结尾处加一个标识符(1)
a = np.array([3,2,1,2,3,4,6]) b = np.r_[1, np.diff(a)!=1, 1] b # 结果:array([1, 1, 1, 0, 0, 0, 1, 1], dtype=int32)
然后用nonzero返回非零数的索引
c = np.nonzero(b)
(array([0, 1, 2, 6, 7], dtype=int64),)
最后用max函数得到距离最远的索引
d = np.diff(c).max() # 正确结果:4