#朴素贝叶斯定力
import numpy as np
import pandas as pd
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
data = pd.read_csv('./010-data_multivar.csv',header=None)
#拆分数据
dataset_X,dataset_y = data.iloc[:,:-1],data.iloc[:,-1]
# print(dataset_X.head())
dataset_X = dataset_X.values
dataset_y = dataset_y.values
# print(dataset_y)
#将标签去重
classes = list(set(dataset_y))
print(classes)
#数据集可视化
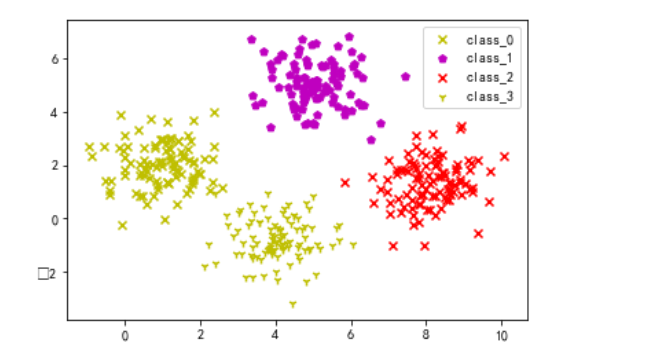
def visual_2D_dataset(dataset_X,dataset_y):
'''将二维数据集dataset_X和对应的类别dataset_y显示在散点图中'''
assert dataset_X.shape[1]==2,'only support dataset with 2 features'
plt.figure()
classes=list(set(dataset_y))
markers=['.',',','o','v','^','<','>','1','2','3','4','8'
,'s','p','*','h','H','+','x','D','d','|']
colors=['b','c','g','k','m','w','r','y']
for class_id in classes:
one_class=np.array([feature for (feature,label) in
zip(dataset_X,dataset_y) if label==class_id])
plt.scatter(one_class[:,0],one_class[:,1],marker=np.random.choice(markers,1)[0],
c=np.random.choice(colors,1)[0],label='class_'+str(class_id))
plt.legend()
visual_2D_dataset(dataset_X,dataset_y)
# 将分类器绘制到图中
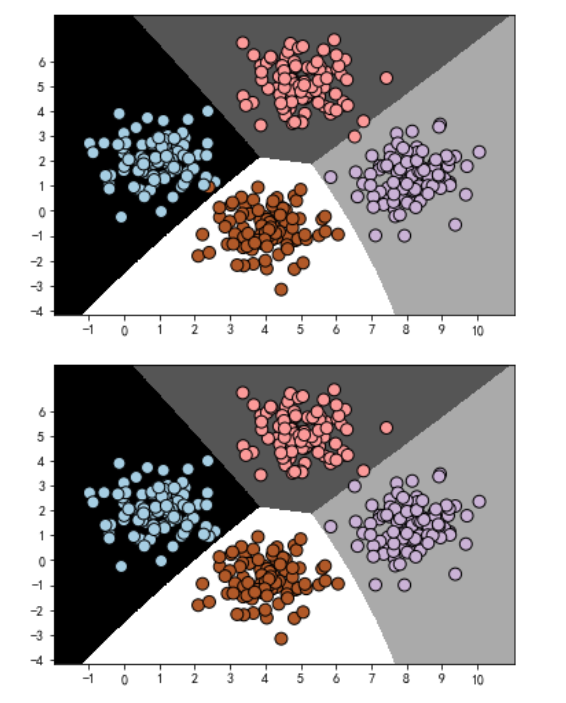
def plot_classifier(classifier, X, y):
x_min, x_max = min(X[:, 0]) - 1.0, max(X[:, 0]) + 1.0 # 计算图中坐标的范围
y_min, y_max = min(X[:, 1]) - 1.0, max(X[:, 1]) + 1.0
step_size = 0.01 # 设置step size
x_values, y_values = np.meshgrid(np.arange(x_min, x_max, step_size), np.arange(y_min, y_max, step_size))
# 构建网格数据
mesh_output = classifier.predict(np.c_[x_values.ravel(), y_values.ravel()])
mesh_output = mesh_output.reshape(x_values.shape)
plt.figure()
plt.pcolormesh(x_values, y_values, mesh_output, cmap=plt.cm.gray)
plt.scatter(X[:, 0], X[:, 1], c=y, s=80, edgecolors='black', linewidth=1, cmap=plt.cm.Paired)
# specify the boundaries of the figure
plt.xlim(x_values.min(), x_values.max())
plt.ylim(y_values.min(), y_values.max())
# specify the ticks on the X and Y axes
plt.xticks((np.arange(int(min(X[:, 0])-1), int(max(X[:, 0])+1), 1.0)))
plt.yticks((np.arange(int(min(X[:, 1])-1), int(max(X[:, 1])+1), 1.0)))
plt.show()
from sklearn.naive_bayes import GaussianNB
gaussian = GaussianNB()
gaussian.fit(dataset_X,dataset_y)
# 预测
y_pre = gaussian.predict(dataset_X)
# print(y_pre)
# 统计判断预测结果和真实值得匹配数量
correct_count = (dataset_y == y_pre).sum()
# print(correct_count)
# print(type(dataset_y))
# print(dataset_y == y_pre)
# 调用绘图函数
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plot_classifier(gaussian,dataset_X,dataset_y)
plot_classifier(gaussian,dataset_X,y_pre)
# 预习分类模型评估指标
#多项式朴素贝叶斯模型
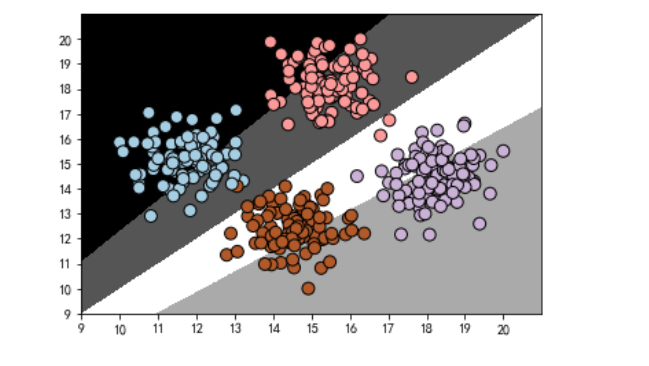
from sklearn.naive_bayes import MultinomialNB from sklearn.preprocessing import MinMaxScaler #范围缩放 scalar = MinMaxScaler(feature_range=(10,20)) dataset_X = scalar.fit_transform(dataset_X) # print(dataset_X) # 要求所有特征必须是非负数,否则没法训练 mul_nb = MultinomialNB() mul_nb.fit(dataset_X,dataset_y) print(np.r_[dataset_X,dataset_y.reshape(-1,2)]) #row方向合并 print(np.c_[dataset_X,dataset_y]) #colume:列向合并 y_pre = mul_nb.predict(dataset_X) #预测 print(y_pre) plot_classifier(mul_nb,dataset_X,dataset_y)

#伯努利贝叶斯模型
from sklearn.naive_bayes import BernoulliNB clf = BernoulliNB() clf.fit(dataset_X,dataset_y) y_pre=clf.predict(dataset_X) print(y_pre) plot_classifier(clf,dataset_X,dataset_y)