在上篇博客中提到,神经网络可以使用梯度下降法求解。因此,在这里对梯度下降法的具体过程进行一些介绍。
首先我们从一个简单的问题出发。假设有一个二元目标函数C(v),其有两个变量v1和v2,其函数图像如下图所示,那么我们如何求解使得目标函数最小时的v1和v2值呢?
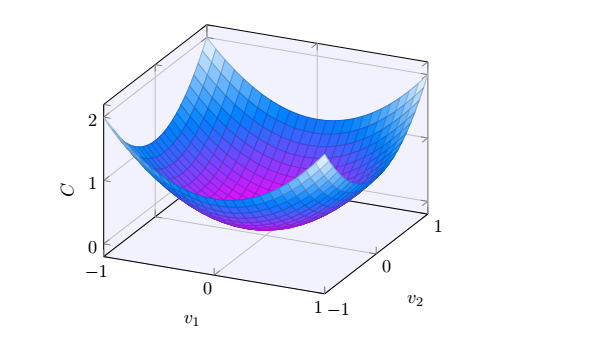
当然一种简单的方法,就是利用微积分的知识,对目标函数求导数,然后使导数为零,得到极值点。但是当目标函数的变量很多,例如神经网络模型,这种方法则很难求解。因此梯度下降法就发挥作用。
梯度下降法求解
首先,我们直观的表述一下梯度下降法求解的过程。即可以将上述二次函数想像成一个山谷。而二次函数的值就是一个小球。那么我们怎么样让小球滚到山谷,即目标函数的最小值呢。我们可以先随机的给小球选择一个出发的位置,然后给每次给它选择一个朝向山谷的方向,让它一步步的滚向山谷。如下图所示,经过若干步以后最终肯定能到山谷。
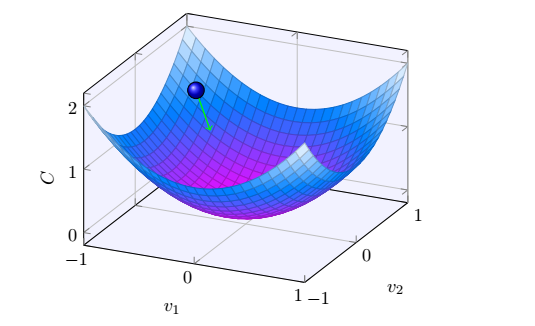
接下来,我们更加形式化的来描述这个问题。假设我们让球分别在v1和v2的方向上移动了很小的量,即Δv1和Δv2,那么球体移动的距离是多少呢?根据微积分的知识,我们可以得到:
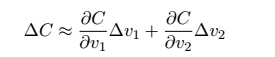
因此,任务就变成了寻找到一种选择Δv1和Δv2的方法,使得ΔC始终为负,即目标函数始终在减小的方法。接下来,我们使用向量的形式来表达上式:
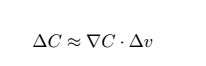 其中,
其中,![]() ,
,![]()
通过向量表达的式子,我们很容易发现,只要取![]() ,,其中η为正数,代表学习率。我们就可以始终保证ΔC为负。也就达到了我们的目标,即目标函数不断的变小。
,,其中η为正数,代表学习率。我们就可以始终保证ΔC为负。也就达到了我们的目标,即目标函数不断的变小。
因此,我们利用![]() 来定义球体在梯度下降算法下的运动规律。,也就是利用其计算Δv,求得球体下一次移动到的位置。
来定义球体在梯度下降算法下的运动规律。,也就是利用其计算Δv,求得球体下一次移动到的位置。
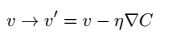
总结一下,梯度下降算法的过程就是不听的计算![]() ,然后沿着相反的方向移动,最终得到目标函数的近似最优解。
,然后沿着相反的方向移动,最终得到目标函数的近似最优解。
上面我们给出了简单的二元函数的梯度下降算法的求解方法。这种方法很容易的能够推广到求解神经网络中,其变量的更新规则和上述相同。如下式所示。
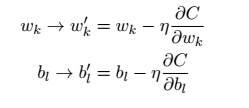
随机梯度下降法
在利用梯度下降法求解神经网络等问题时,我们可以发现在每次更新变量,计算梯度时,我们需要对整个数据集中的每个样本计算梯度,然后在求和。这对于数据量很小的数据集来说还可以接受,一旦数据规模很大时,学习将变得非常缓慢。因此,随机梯度下降法应运而生。
其主要思想是随机选取小量的询量输入样本来计算![]() ,进而估计
,进而估计![]() ,通过计算商量样本的平均值我们可以快速得到一个对于实际梯度
,通过计算商量样本的平均值我们可以快速得到一个对于实际梯度![]() 很好的估计,这样有加速学习过程。因此,我们可以得到随机梯度下降法的计算公式如下所示:
很好的估计,这样有加速学习过程。因此,我们可以得到随机梯度下降法的计算公式如下所示:
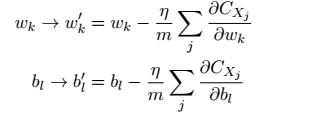
其中,m表示随机选取样本的数量。