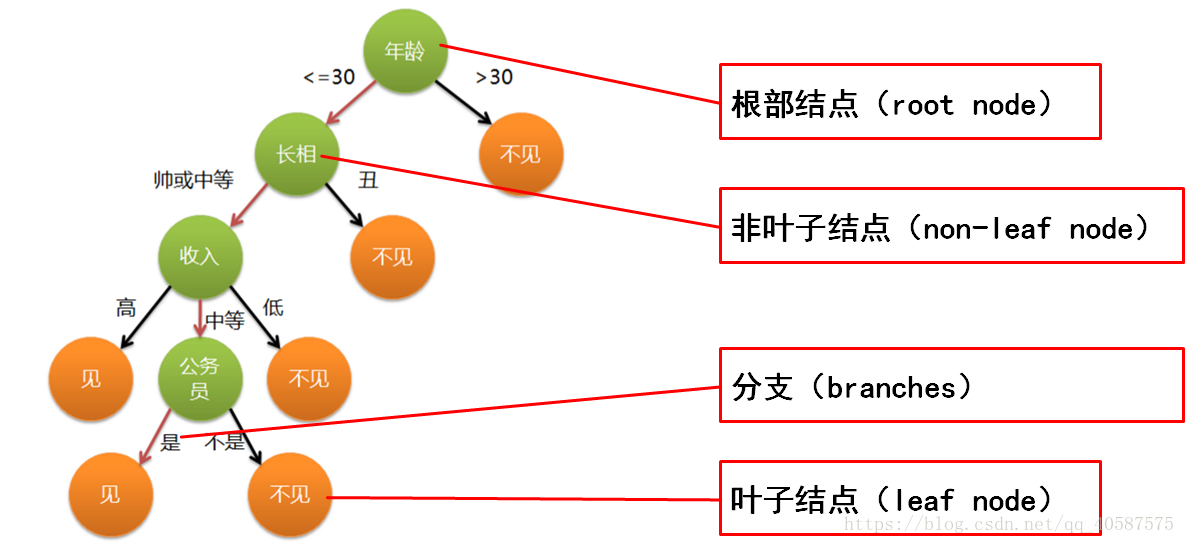
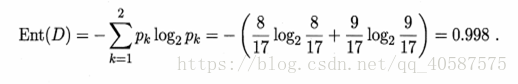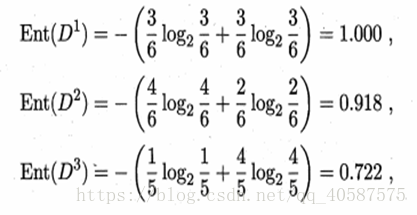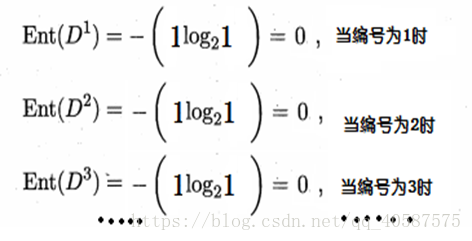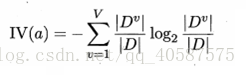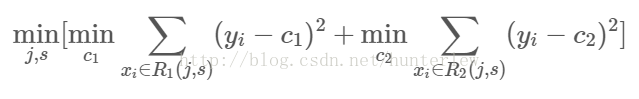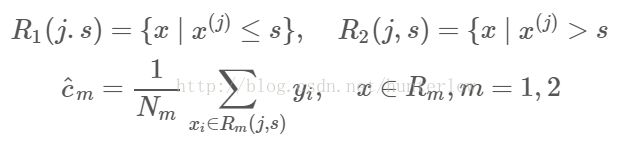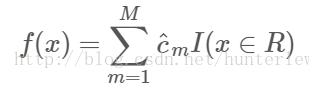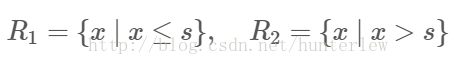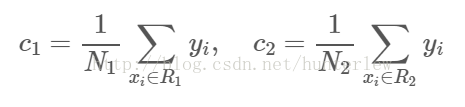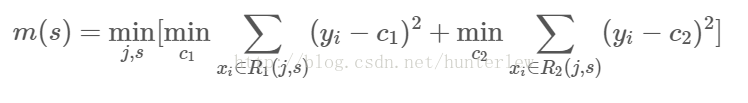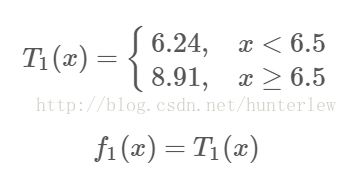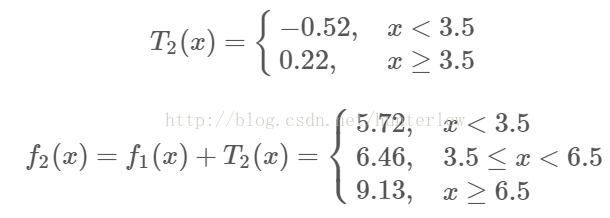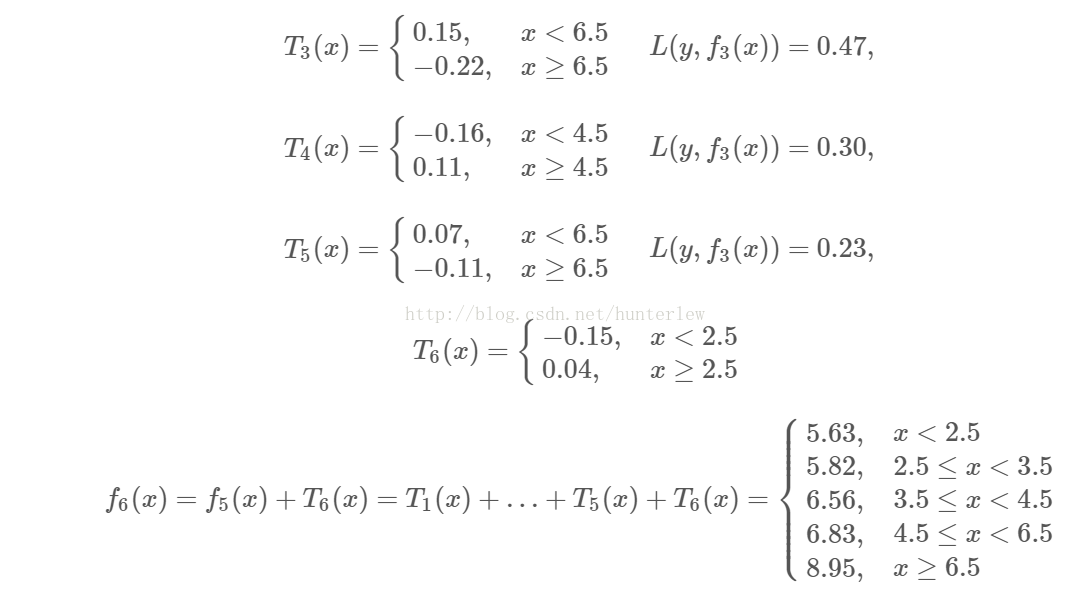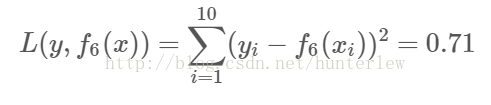1.什么是决策树：
决策树是以树状结构表示数据分类的结果
非叶子结点代表测试的条件。
分支代表测试的结果
2.如何构建决策树：
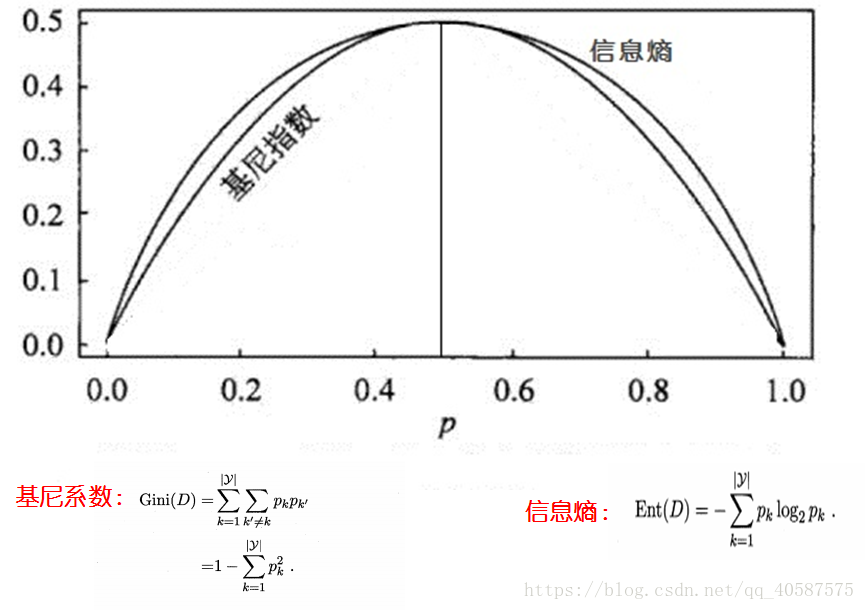
´1.信息熵（informationentropy）：是度量样本集合纯度最常用的一种指标。
2.基尼系数（gini）：是度量样本集合不确定性指标。（基尼指数与熵可近似看做是统一概念，都是越大，确定性越差）
基尼指数和信息熵的图像：（当熵和基尼指数为0.5时，即确定某件事的概率为50%，是最不能肯定的事件。如：小明后天再路上捡钱的概率为50%，很不确定。如果概率为30%，代表很可能捡不到钱；如果概率为60%，则代表更可能捡到钱。）
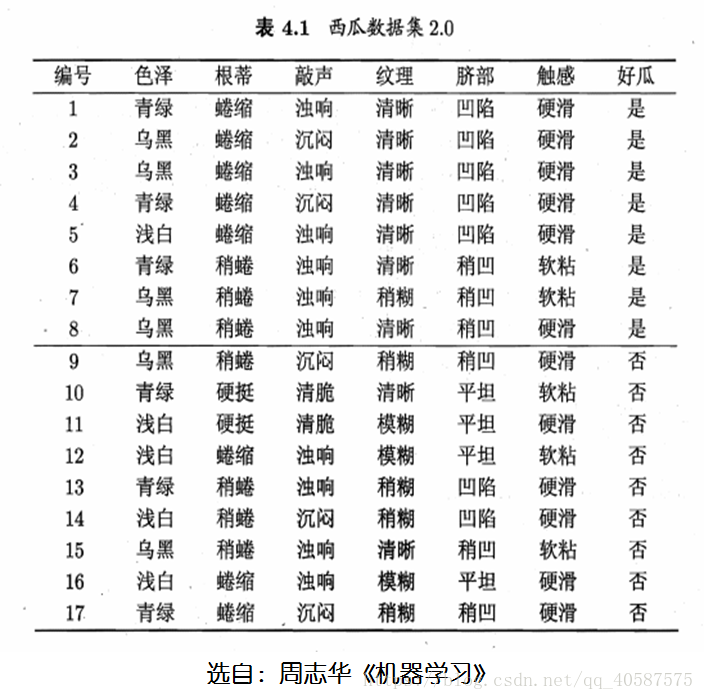
一个小栗子：
1.系统信息熵：（是，否为好瓜的两个属性）
2.每个特征的信息熵：（以色泽为例）（先计算出3 个属性的信息熵，依次为：青绿，乌黑，浅白）
然后，结合3 个属性，计算出特征为色泽的信息熵。
3.信息增益：
信息增益大，代表着熵小，所以确定性较高。
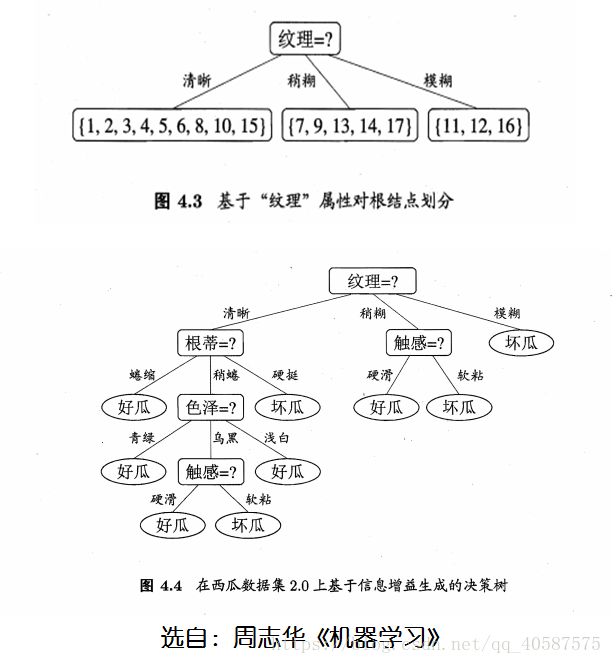
得出决策结果
但是，当我们使用ID编号作为一个特征量的时候
´得到信息熵：
´信息增益为：
所以需要使用编号作为根节点吗？显然不可能。
（所以说：ID3决策树倾向于选择属性较多的特征，当这个特征不一定是最优的属性特征。同时，ID3决策树只能处理离散的属性，对于连续的属性，需要在 分类前对其进行离散化。）
C4.5算法：
ID3算法不能处理连续特征， C4.5的思路是将连续的特征离散化。比如 m 个样本的连续特征 A 有m个，从小到大排列为a1,a2,...,am则 C4.5取相邻两样本值的平均数，一共取得 m-1个 划分点，其中第 i 个划分点 Ti 表示为：。对于这m-1 个点，分别计算以该点作为二元分类点时的信息增益 。选择信息增益最大的点作为该连续特征的二元离散分类点。比如取到的增益最大的点为
,则小于
的值为类别1，大于
的值为类别2，这样我们就做到了连续特征的离散化。要注意的是，与离散属性不同的是，如果当前节点为连续属性，则该属性后面还可以参与子节点的产生选择过程。
因此，引入增益率：
求得IV（编号）：
´=1/(17)*17*log2（1/(17)）=4.08
´如果一个特征的取值越多，其IV(a)分母也越大。
对于缺失值的解决办法：
没有缺失值的数据单纯只是计算一次系统熵不同，有缺失值的需要依据不同的缺失值的权重，计算不同的特征的熵
1. 将有缺失值的属性分别分配到所有的分支上，计算缺失值的权重
2. 依据新的缺失值的权重计算该特征的熵，计算各属性的熵
3. 计算没有缺失值与总的属性数的比重，乘以没有缺失值的信息增益
scikit-learn中使用的算法就是CART 算法，既能进行模型分类，也可以进行模型的回归。
|
决策树常见算法 |
ID3算法 |
C4.5算法 |
CART算法 |
|
结点选择准则 |
信息增益 |
信息增益率 |
基尼系数 |
使用基尼系数作为特征划分规则时：
上述使用jini指数作为特征分类标准时，以特定的一个属性作为一部分，另外的全部属性作为另外一部分，来计算jini指数。
《统计学习》中CART树的gini指数计算：
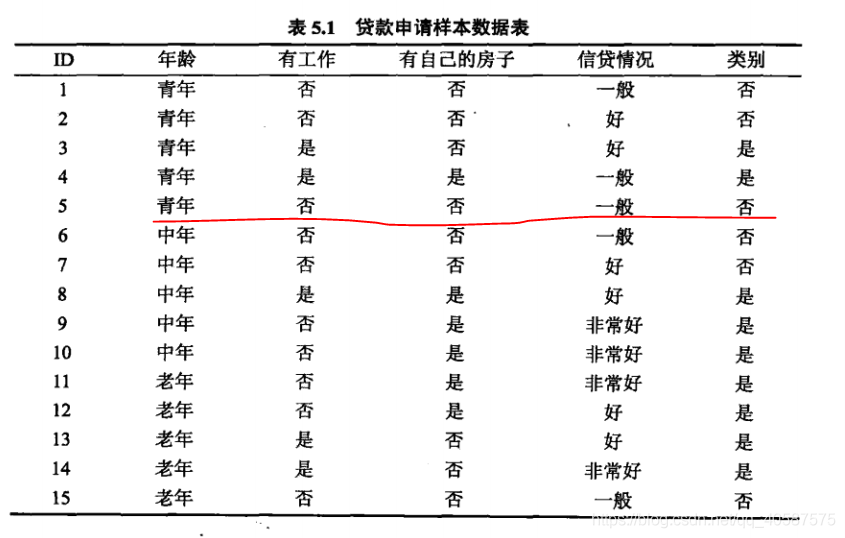
计算的表格数据，是一个分类问题：
计算最佳的特征值和属性值
CART 回归树：
原文链接：https://cethik.vip/2016/09/21/machineCAST/
一、概念
CART全称叫Classification and Regression Tree。首先要强调的是CART假设决策树是二叉树，内部结点特征的取值只有“是”和“否”，左分支是取值为“是”的分支，有分支则相反。这样的决策树等价于递归地二分每个特征。
二、CART生成
决策树的生成就是递归地构建二叉决策树的过程，对回归树用平方误差最小化准则，对分类树用基尼指数最小化准则，进行特征选择，生成二叉树。
三、回归树的生成最小二叉回归树生成算法：
1、选择最优切分变量j与切分点s，求解：
遍历变量j，对固定的切分变量j扫描切分点s，选择使上式取得最小值的对(j,s)。其中Rm是被划分的输入空间，Cm空间Rm对应的输出值。
2、用选定的对(j,s)划分区域并决定相应的输出值：
3、继续对两个子区域调用步骤1，直至满足停止条件。
4、将输入空间划分为M个区域R1,R2,...Rm生成决策树：
对于决策树建立后做预测的方式，CART分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。而回归树输出不是类别，它采用的是用最终叶子的均值或者中位数来预测输出结果。
CART回归树和CART分类树的建立算法和预测没有什么很大区别。
四、示例
上面的东西有点难以理解，下面举个例子来说明。
训练数据见下表，x的取值范围为区间[0.5,10.5]，y的取值范围为区间[5.0,10.0]，学习这个回归问题的最小二叉回归树。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 5.56 | 5.70 | 5.91 | 6.40 | 6.80 | 7.05 | 8.90 | 8.70 | 9.00 | 9.05 |
求解训练数据的切分点s:
容易求得在R1、R2内部使得平方损失误差达到最小值的c1、c2为：
这里N1、N2是R1、R2的样本点数。
求训练数据的切分点，根据所给数据，考虑如下切分点：
1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5。
对各切分点，不难求出相应的R1、R2、c1、c2及
例如，当s=1.5时，R1={1}，R2={2,3,...,10}，c1=5.56，c2=7.50，则
现将s及m(s)的计算结果列表如下：
| s | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
|---|---|---|---|---|---|---|---|---|---|
| m(s) | 15.72 | 12.07 | 8.36 | 5.78 | 3.91 | 1.93 | 8.01 | 11.73 | 15.74 |
由上表可知，当x=6.5的时候达到最小值，此时R1={1,2,...,6}，R2={7,8,9,10}，c1=6.24，c2=8.9，所以回归树T1(x)为：
用f1(x)拟合训练数据的残差见下表，表中r2i=yi-f1(xi),i=1,2,...,10
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| -0.68 | -0.54 | -0.33 | 0.16 | 0.56 | 0.81 | -0.01 | -0.21 | 0.09 | 0.14 |
第2步求T2(x)方法与求T1(x)一样，只是拟合的数据是上表的残差，可以得到：
继续求得
可以用拟合训练数据的平方损失误差等来作为结束条件。此时
假设此时已经满足误差要求，那么f(x)=f6(x)即为所求的回归树。
CART分类树：
算法输入是训练集D，基尼系数的阈值，样本个数阈值。
输出是决策树T。
我们的算法从根节点开始，用训练集递归的建立CART树。
1) 对于当前节点的数据集为D，如果样本个数小于阈值或者没有特征，则返回决策子树，当前节点停止递归。
2) 计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归。
3) 计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数，对于离散值和连续值的处理方法和基尼系数的计算、缺失值的计算方法不同。
4) 在计算出来的各个特征的各个特征值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值，把数据集划分成两部分D1和D2，同时建立当前节点的左右节点，做节点的数据集D为D1，右节点的数据集D为D2.
5) 对左右的子节点递归的调用1-4步，生成决策树。
对于生成的决策树做预测的时候，假如测试集里的样本A落到了某个叶子节点，而节点里有多个训练样本。则对于A的类别预测采用的是这个叶子节点里概率最大的类别。
三种决策树算法的比较：
| 算法 | 支持模型 | 树结构 | 特征选择 | 连续值处理 | 缺失值处理 | 剪枝 |
| ID3 | 分类 | 多叉树 | 信息增益 | 不支持 | 不支持 | 不支持 |
| C4.5 | 分类 | 多叉树 | 信息增益率 | 支持 | 支持 | 支持 |
| CART | 分类，回归 | 二叉树 | 基尼系数，均方差 | 支持 | 支持 | 支持 |
决策树算法的优缺点：
1.决策树算法的优点：
1）简单直观，生成的决策树很直观。
2）基本不需要预处理，不需要提前归一化，处理缺失值。
3）使用决策树预测的代价是O(log2m)。 m为样本数。
4）既可以处理离散值也可以处理连续值。很多算法只是专注于离散值或者连续值。
5）可以处理多维度输出的分类问题。
6）相比于神经网络之类的黑盒分类模型，决策树在逻辑上可以得到很好的解释
7）可以交叉验证的剪枝来选择模型，从而提高泛化能力。
8） 对于异常点的容错能力好，健壮性高。
2.决策树算法的缺点:
1）决策树算法非常容易过拟合，导致泛化能力不强。可以通过设置节点最少样本数量和限制决策树深度来改进。
2）决策树会因为样本发生一点点的改动，就会导致树结构的剧烈改变。这个可以通过集成学习之类的方法解决。
3）寻找最优的决策树是一个NP难的问题，我们一般是通过启发式方法，容易陷入局部最优。可以通过集成学习之类的方法来改善。
4）有些比较复杂的关系，决策树很难学习，比如异或。这个就没有办法了，一般这种关系可以换神经网络分类方法来解决。
5）如果某些特征的样本比例过大，生成决策树容易偏向于这些特征。这个可以通过调节样本权重来改善。
此处 三种决策树的比较 和 决策树的优缺点 均来自于 刘建平的blog
对于不能解决异或问题的理解：
4组数据：
（0,1）输出1
（1,0）输出1
（0,0）输出1
（1,1）输出1
由于决策树的划分都是横纵的，可以画图知道，决策树不能解决异或问题。
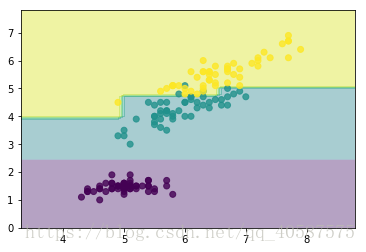
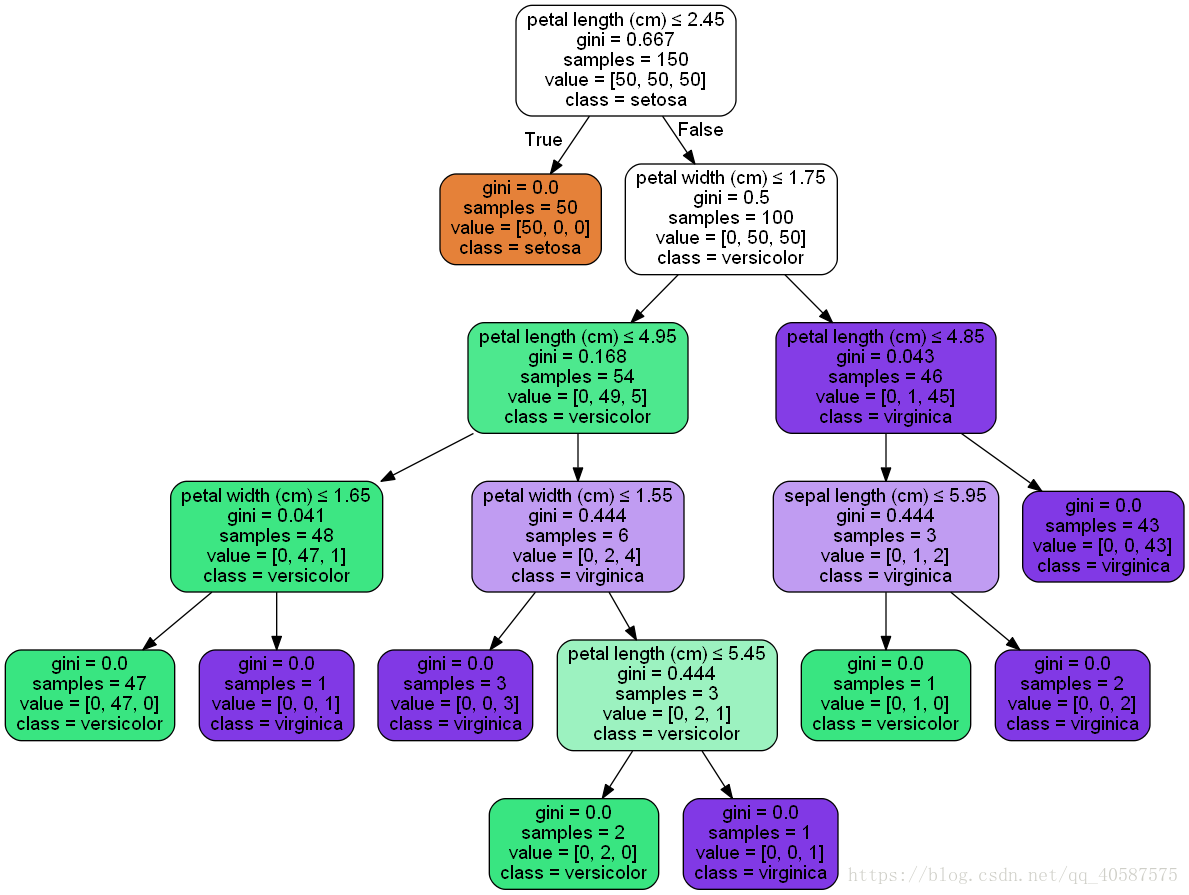
实例：
#coding=gbk
#使用ID3决策树预测销量的高低,基于信息熵
import pandas as pd
filename = r'D:datasetssales_data.xls'
data = pd.read_excel(filename, index_col= u'序号') #将序号作为索引
data[data == u'好'] = 1 #使用1 表示‘好’，是，高，3个属性
data[data == u'是'] = 1
data[data == u'高'] = 1
data[data != 1] = -1
print(data.head())
# 序号 天气 是否周末 是否有促销 销量
# 1 -1 1 1 1
# 2 -1 1 1 1
# 3 -1 1 1 1
# 4 -1 -1 1 1
# 5 -1 1 1 1
x = data.iloc[:,:3].as_matrix().astype(int) #将前3列作为输入
y = data.iloc[:,3].as_matrix().astype(int)#最后列作为标签
#建立决策树
from sklearn.tree import DecisionTreeClassifier as DTC
dtc = DTC(criterion='entropy') #建立决策树，基于信息熵
dtc.fit(x,y)
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
x = pd.DataFrame(x)
with open(r'D:datasets ree.dot','w') as f:
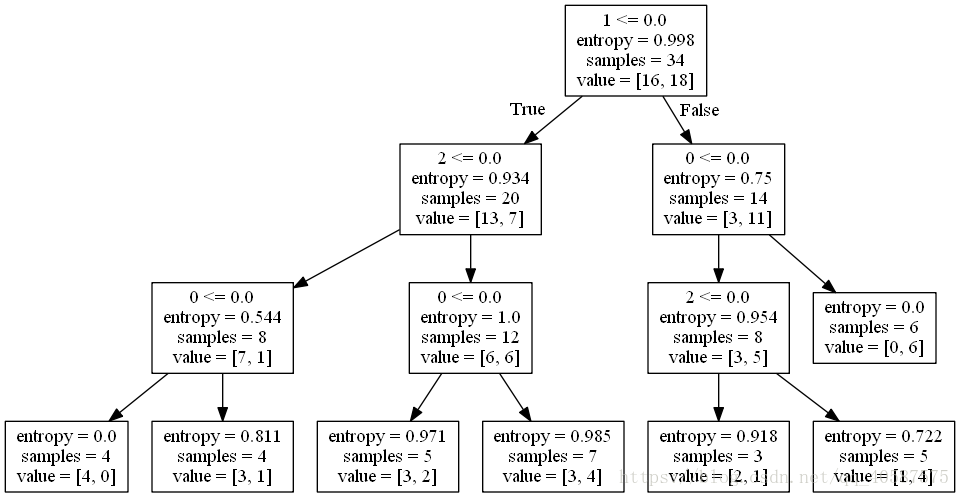
f = export_graphviz(dtc, feature_names=x.columns, out_file=f)安装Graphviz，显示决策树图像，可参考一篇博客
进入windows命令行界面，cd 切换到tree.dot所在的路径，执行
dot -Tpng tree.dot -o tree.png可获取图像：
print('------test-------')
from itertools import product
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
X = iris.data[:, [0,2]]
y = iris.target
clf = DecisionTreeClassifier(max_depth=4)
clf.fit(X, y)
x_min, x_max = X[:, 0].min()-1, X[:, 0].max()+1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
print(x_min, x_max)
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))
print(xx.shape)
print(xx)
print(yy)
print(yy.shape)
z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
plt.contourf(xx, yy, z, alpha=0.4)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.8)
plt.show()
#对iris 数据进行可视化：
from IPython.display import Image
from sklearn import tree
import pydotplus
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target
clf = tree.DecisionTreeClassifier()
clf.fit(X, y)
dot_data = tree.export_graphviz(clf, out_file=None, feature_names=iris.feature_names,
class_names = iris.target_names, filled=True,
rounded=True, special_characters=True
)
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png())
使用下列程序，将其输出到指定文件。
graph.write_pdf('D:\datasetsiris.pdf')决策树的参数：
sklearn.tree.DecisionTreeClassifier
(criterion='gini', splitter='best', max_depth=None, min_samples_split=2,
min_samples_leaf=1,min_weight_fraction_leaf=0.0, max_features=None,
random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, class_weight=None, presort=False)criterion:特征选择的标准，有信息增益和基尼系数两种，使用信息增益的是ID3和C4.5算法（使用信息增益比），使用基尼系数的CART算法，默认是gini系数。
splitter:特征切分点选择标准，决策树是递归地选择最优切分点，spliter是用来指明在哪个集合上来递归，有“best”和“random”两种参数可以选择，best表示在所有特征上递归，适用于数据集较小的时候，random表示随机选择一部分特征进行递归，适用于数据集较大的时候。
max_depth:决策树最大深度，决策树模型先对所有数据集进行切分，再在子数据集上继续循环这个切分过程，max_depth可以理解成用来限制这个循环次数。
min_samples_split:子数据集再切分需要的最小样本量，默认是2，如果子数据样本量小于2时，则不再进行下一步切分。如果数据量较小，使用默认值就可，如果数据量较大，为降低计算量，应该把这个值增大，即限制子数据集的切分次数。
min_samples_leaf:叶节点（子数据集）最小样本数，如果子数据集中的样本数小于这个值，那么该叶节点和其兄弟节点都会被剪枝（去掉），该值默认为1。
min_weight_fraction_leaf:在叶节点处的所有输入样本权重总和的最小加权分数，如果不输入则表示所有的叶节点的权重是一致的。
max_features:特征切分时考虑的最大特征数量，默认是对所有特征进行切分，也可以传入int类型的值，表示具体的特征个数；也可以是浮点数，则表示特征个数的百分比；还可以是sqrt,表示总特征数的平方根；也可以是log2，表示总特征数的log个特征。
random_state:随机种子的设置，与LR中参数一致。
max_leaf_nodes:最大叶节点个数，即数据集切分成子数据集的最大个数。
min_impurity_decrease:切分点不纯度最小减少程度，如果某个结点的不纯度减少小于这个值，那么该切分点就会被移除。
min_impurity_split:切分点最小不纯度，用来限制数据集的继续切分（决策树的生成），如果某个节点的不纯度（可以理解为分类错误率）小于这个阈值，那么该点的数据将不再进行切分。
class_weight:权重设置，主要是用于处理不平衡样本，与LR模型中的参数一致，可以自定义类别权重，也可以直接使用balanced参数值进行不平衡样本处理。
presort:是否进行预排序，默认是False，所谓预排序就是提前对特征进行排序，我们知道，决策树分割数据集的依据是，优先按照信息增益/基尼系数大的特征来进行分割的，涉及的大小就需要比较，如果不进行预排序，则会在每次分割的时候需要重新把所有特征进行计算比较一次，如果进行了预排序以后，则每次分割的时候，只需要拿排名靠前的特征就可以了。
函数方法：
decision_path(X):返回X的决策路径
fit(X, y):在数据集(X,y)上使用决策树模型
get_params([deep]):获取模型的参数
predict(X):预测数据值X的标签
predict_log_proba(X):返回每个类别的概率值的对数
predict_proba(X):返回每个类别的概率值（有几类就返回几列值）
score(X,y):返回给定测试集和对应标签的平均准确率