另一个选址模型
假设有两个小镇,本别称为东镇和西镇,每个小镇最多能容纳10万人,然后我们假设世界上一共有20万人,他们一共有两种人,分别是大个子和小个子。策略是你选择东镇还是西镇。利润与参与者所属人群在所在小镇的人数呈如下关系。并且我们假定如果某个小镇的人数超过10万,我们会采取随机策略选出一部分多出的人将他们移到另一个小镇。
每个人获得的利润与他所在的小镇中他的同类人群的人数的关系如下:
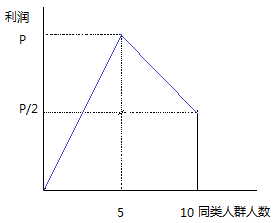
这里的纳什均衡一共有三个:
- 大个子全都集中在东镇,小个子全都集中在西镇;或者大个子全都集中在西镇,小个子全都集中在东镇。
- 因为当初始情况不平等时,那些在城镇中占少数人群的人为了获得最大利润或选择去另一个城镇,从而导致了 -- 种族隔离
- 每个小镇的大个子和小个子的比例刚好是50%/50%。
- 这种情况下大家都达到最大利润。这其实是一种弱纳什均衡,因为微笑的改动很可能导致趋势像上者转移。
- 所有的人都搬到东镇或者所有的人都搬到了西镇。
- 这种情况下将随机选择出50%的人移向另一个小镇。因为根据大数定理,随机产生的人群里面大个子和小个子的比例接近于50%/50%
结论:
- 有的时候从限制条件可以得到纳什均衡,如上述的策略随机化
石头剪刀布 Rock, Scissor and Paper
| R | S | P | |
| R | 0,0 | 1,-1 | 1,-1 |
| S | -1,1 | 0,0 | 1,-1 |
| P | 1,-1 | 0,0 | -1,1 |
这里我出石头剪刀和布的期望都为(+1)*1/3+(-1)*1/3+0*1/3=0 所以这里的纳什均衡是: 以1/3的概率随机出石头,见到或布。 -- 策略随机化