一、使用随机森林对系统参数进行故障诊断
1、模型选择
sklearn的随机森林+多输出结果模型
model = MultiOutputClassifier(RandomForestClassifier())
2、模型类型
属于分类模型,即判断系统的n个参数是否正确,或是否属于特定的类型。
举例:如参数是否属于正常的范围0~100之内,或者参数属于状态【正常、警告、故障】中的哪一状态
3、模型建立过程
提供系统n个参数的拟合数据=参数取值数据+结果标签数据,不能欠拟合和过拟合的数据,否则诊断结果可能出现误诊的情况。
举例:一个系统有3个参数温度a、整机状态b、传感器状态c,参数定义如下
温度a取值20~30正常、低于20和高于30异常; # 20~30、小于20、大于20为参数取值数据,正常、异常是结果标签数据
整机状态b取值0为正常、1为异常; # 0、1为参数取值数据,正常、异常为结果标签数据
传感器状态c取值0为正常、1为警告、2为故障 # 0、1、2为参数取值数据,正常、警告、故障为结果标签数据
拟合数据和结果标签数据:
| 参数取值数据 | 结果标签数据 |
| [25, 0, 0] |
[正常, 正常, 正常] |
| [30, 1, 0] |
[异常, 异常, 正常] |
| [25, 0 , 2] |
[正常, 正常, 故障 |
| ... | ... |
这样的数据需要足够多,如产生10万条数据,能将实际可能产生的数据都囊括完。产生了拟合数据之后,将数据输入给模型即可完成建模。
注意:产生数据的原则就是数据不要出现欠拟合和过拟合的情况。
欠拟合数据:
只产生了100条数据,不能囊括所有情况;特征数据太少,如一个系统本应由10个参数决定状态,这里只有3个参数。【通过增加数据和特征值解决】
过拟合数据:
产生的数据有错误,如把温度取值100当做了正常;特征值过多,如一个系统本应由2个参数决定状态,这里有3个【通过增加正确数据,减少噪声(多余的特征值)解决】
4、参数诊断及定位
通过输入真实参数取值到模型,模型即可输出对应的标签。如
输入:[25, 0, 0]
模型输出:[正常, 正常, 正常]
5、关于迭代
如有一天因为环境产生了变化,温度正常范围从20~30变成了25~35,重新生成拟合数据重新建模。可将新拟合数据追加到老拟合数据来建模【理论上这样不够正常,但貌似没有更好的方法,因为建模是需要大量时间、CPU资源的过程】
二、使用线性回归对系统参数进行故障诊断
1、模型选择
sklearn的线性回归
lr = LinearRegression()
2、其他和随机森林类似
模型类型、模型建立过程、参数诊断及定位和上面随机森林皆一致
3、不同之处
随机森林将大量的数据进行简单的分类,是1就是1,是2就是2,然后根据输入的真实数据,在模型中匹配最佳可能结果标签,然后输出最大概率的诊断结果
而线性回归认为,某一时刻的取值和历史的取值是有关系的,如下一时刻的取值可能和历史的100次取值相关,然后根据以前的取值来进行当前的诊断。
可根据实际情况选择不同模型。
三、时间序列分析之使用GM11&GM21完成对单参数的预测
1、模型选择
greytheory的gm11【gm21还未在实际项目中使用】
grey = GreyTheory()
gm11 = grey.gm11
2、模型类型
对单个参数的预测,单调性参数使用gm11,周期性参数使用gm21【随机性参数使用gm31】
如判断一个单调性参数1天后取值是多少。
3、模型建立过程
输入参数的n个等距历史取值,相邻参数的时间片为预测时间,如每隔1天取1个参数取值,共取1000次,那么gm11最后的输出结果为:预测最后一个数据之后一天的取值。
举例:
某个单调增的参数,如一个城市的人口数,从今天器往前每隔1天取1次数,取1000次:
| 时间 | 人口数 |
| 第一天 | 1000000 |
| 第二天 | 1000100 |
| ... | ... |
如果取值越多、间隔越小,预测结果越准确。
4、参数预测
输入:今天之前每隔1天取值,共1000次取值
模型输出:今天作为起点,1天之后的人口数预测
5、关于迭代
无法迭代,gm11是属于数学公式计算,需要每次输入多个历史取值,根据历史取值推测数下一个取值。
四、结合正态分布对数据的分析
1、参数对象
具备正态分布取值的数据。一般项目中大多数数据都属于正态分布,参数取值一般有个正常的取值范围A~B,而往往这个参数不会真正取值到A~B,而是集中在这个范围的更小一个范围。如一个器件的额定电压为220V,由于自带过压、欠压保护,即使电压上下浮动20V,也可让器件正常运行,一旦超过20V便可能损坏。而在实际运行中,如果每隔1s对输入电压采样,共采1万次【足够大】,可以发现取值往往在额定电压220V上下2~5V波动【举例,可能更小或更大】,故我们可以认为取值220V的概率更大,随着取值离220V越大,概率越小,也就是正态分布【简单的描述:正态分布就是概率与取值呈现单峰的参数,项目中可以假设一切范围取值类参数都呈正态分布,布尔、枚举类肯定不是】。
2、随机分布和正态分布图例
随机分布认为采样的数据中,200V~240V中任一电压和其他电压出现的频率一致【即概率大致相同】;正态分布认为有一个电压出现频率最高,然后频率向两边取值逐渐降低。
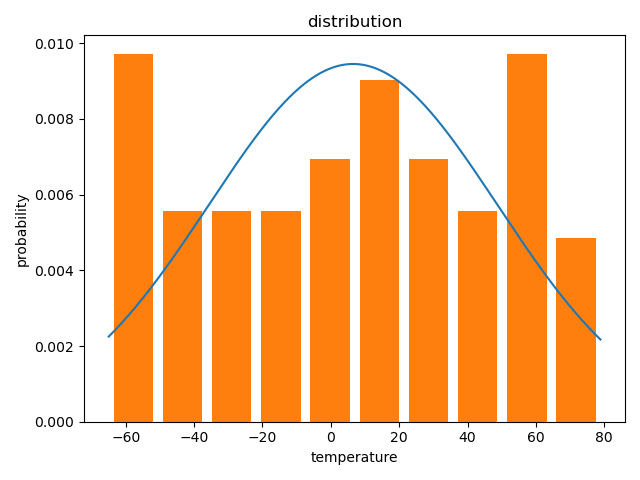
随机分布
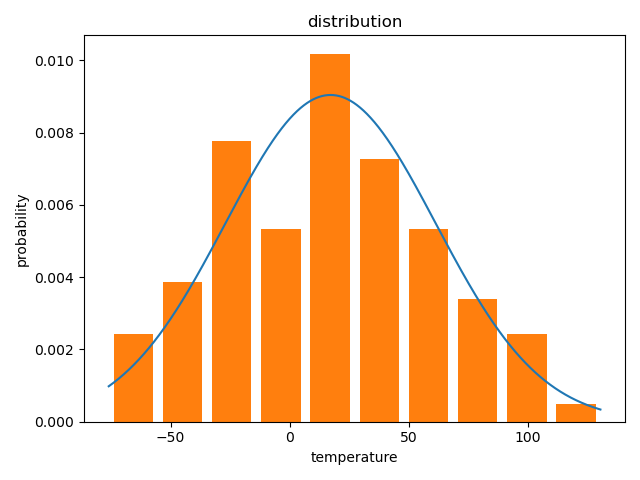
正态分布
3、作用
正态分布与其相关的数学参数,是对参数实际情况的描述,输出对参数的分析结果,而非上文的诊断、预测。
4、参数描述
可直接输出参数的均值、峰值【众数】、中位数、方差、标准差、置信区间【带宽】、异常值等参数,即可一定程度上描述此参数对应时间内的一个走向。
注意:由于参数取值往往是float型的,如果阈值范围较大,建议转化为int类型来处理,否则众数、中位数的结果可能出现问题。如参数范围是100.0~200.0,参数大概率取值范围是150~160,这个区间被取了1000次,由于float类型,可能导致150~160之间分成了很多份,使这个区间的同一数据被取得的次数较少;由于意外100~120之间有个数是110被取到了10次,故众数可能从150~160变成了110。
5、模型选择
numpy【用于数据生成、数据分析】、scipy【判断是否属于正态分布、数据分析】
五、使用梯度下降对系统整机进行故障诊断
1、模型选择
sklearn的SGD模型
model = SGDClassifier(shuffle=True, loss='log')
SGD可在线迭代,可是不能多参数输出
2、模型类型
属于分类模型,即判断系统的n个参数是否正确,或是否属于特定的类型。
举例:如参数是否属于正常的范围0~100之内,或者参数属于状态【正常、警告、故障】中的哪一状态
3、模型建立过程
提供系统n个参数的拟合数据=参数取值数据+结果标签数据,不能欠拟合和过拟合的数据,否则诊断结果可能出现误诊的情况。
举例:一个系统有3个参数温度a、整机状态b、传感器状态c,参数定义如下
温度a取值20~30正常、低于20和高于30异常;
整机状态b取值0为正常、1为异常;
传感器状态c取值0为正常、1为警告、2为故障
此模型只能有一个标签,故定义:只要有一个参数异常,则认为系统整机异常【0为正常,1为异常】
拟合数据和结果标签数据:
| 参数取值数据 | 结果标签数据 |
| [25, 0, 0] |
[0] |
| [30, 1, 0] |
[1] |
| [25, 0 , 2] |
[1] |
| ... | ... |
这样的数据需要足够多,如产生10万条数据,能将实际可能产生的数据都囊括完。产生了拟合数据之后,将数据输入给模型即可完成建模。
注意:产生数据的原则就是数据不要出现欠拟合和过拟合的情况。
欠拟合数据:
只产生了100条数据,不能囊括所有情况;特征数据太少,如一个系统本应由10个参数决定状态,这里只有3个参数。【通过增加数据和特征值解决】
过拟合数据:
产生的数据有错误,如把温度取值100当做了正常;特征值过多,如一个系统本应由2个参数决定状态,这里有3个【通过增加正确数据,减少噪声(多余的特征值)解决】
4、参数诊断及定位
通过输入真实参数取值到模型,模型即可输出对应的标签。如
输入:[25, 0, 0]
模型输出:[0]
5、关于迭代
使用partial_fit即可完成自我学习。
六、时间序列分析之使用指数平滑对单个参数预测
1、无明显单调或周期变化的参数
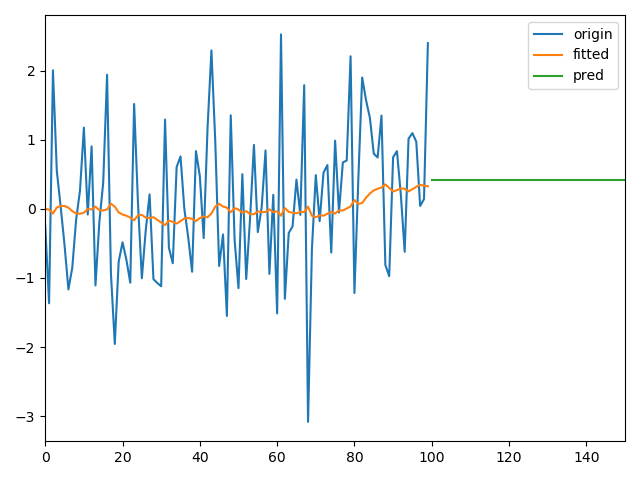
2、单调变化的参数
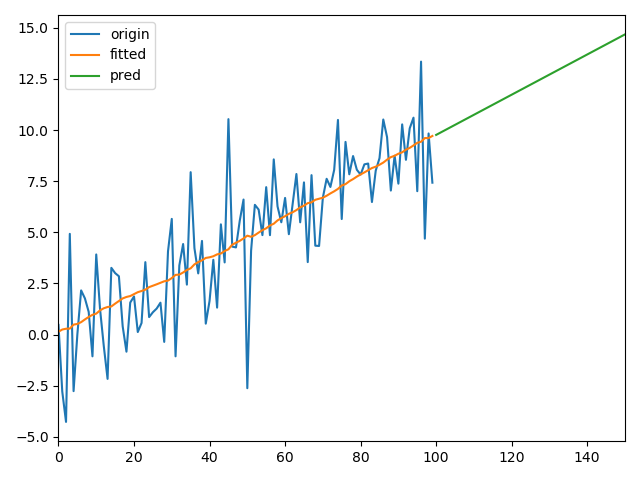
3、周期变化的参数
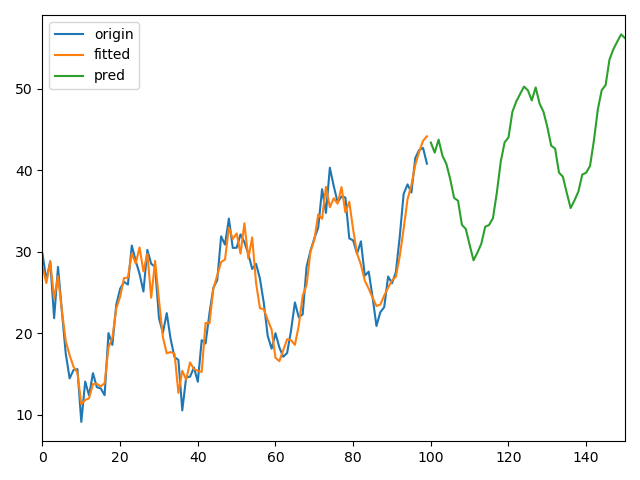
七、判断多个或单个特征参数对另一参数的影响
如海拔、人口、气温对房价的影响
建议使用线性回归