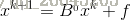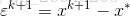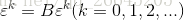机器学习之逐次下降法(机器学习算法原理与实践）郑捷 (P159-p163)

逐次下降法的定义：

1. 对于给定的方程组，使用公式： 
    
   其中k为迭代次数（k=0,1,2,…） 
   逐步代入求近似解的方法称为迭代法
2. 如果存在（记为），称此迭代法收敛，显然就是方程组的解，否则称此迭代法发散。
3. 研究{}的收敛性。引进误差向量： 
    
   得到： 
    
   递推得到： 
    
   要考察{}的收敛性，就要研究B在或的条件。

下面给出Python实现

# -*- coding: utf-8 -*-
import numpy as np
from numpy import *
from common_libs import *
import matplotlib.pyplot as plt

#消元发求解方程组的解
#求解元方程
def method_nomal():
A=mat([[8,-3,2],
[4,11,-1],
[6,3,12]])
b=mat([20,33,36])

result=linalg.solve(A,b.T)
print result

#迭代法进行计算
def interationMethod(n,B0,f):
error = 1.0e-6 # 迭代阈值
steps = 100 # 迭代次数
xk=zeros((n,1))
errorlist=[]
for i in range(steps):
xk_1=xk
xk=B0*xk+f
errorlist.append(linalg.norm(xk_1-xk))
if errorlist[-1]<error:
print i+1
break
print xk
return i,errorlist

method_nomal()
B0=mat([[0.0,3.0/8,-2.0/8],
[-4.0/11,0.0,1.0/11],
[-6.0/12,-3.0/12,0.0]])
print(B0)
f=mat([20.0/8,33.0/11,36.0/12])
[k,errorlist]=interationMethod(3,B0,f)

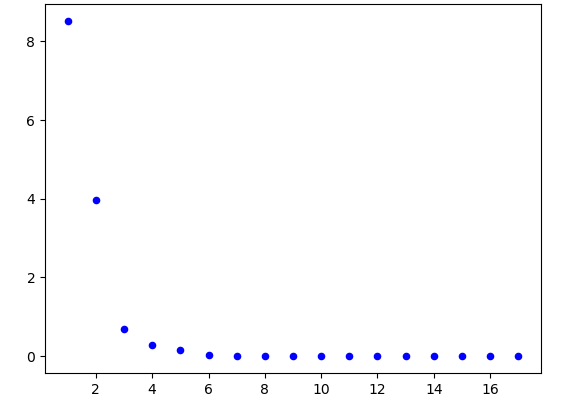
# 绘制散点图
matpts= zeros((2,k+1))
matpts[0]=linspace(1,k+1,k+1)
print matpts[0]
matpts[1]=array(errorlist)
drawScatter(plt,matpts)
plt.show()