什么是树?
没错,就是森林中的树哈哈。其实一两句话很难说清楚这个玩意儿,请自行百度,但是碍于形式,给出一个简单的定义:树有一组以边链接的节点组成。
但是要注意了哈,这个定义给出了很多信息:
1.节点(说明我们要创建一个节点类,代表树中的每一个节点的数据结构)
2.边(就是当前节点指向另一个节点的链接,就是边,提前透露一下,我定义的节点类中left和right就是边)
正如题目所说,是浅谈树,那就不做过多理论上的分析,要想知道理论,还是那句话请自行百度,好吧!。
还多bb一句,树一定是有一个跟节点的。
下面给出树中的每一个节点的数据类型,且看代码:
class Node { constructor(data,left,right) { // 节点保存的数据 this.data = data; // 节点的左子节点 this.left = left; // 节点的右子节点 this.right = right; // 该节点保存的数据出现的次数,默认只出现一次 this.count = 1; } }
看,这就是一个节点的定义,不复杂是吧。这里解释一下为什么说left和right是边,你想这两个属性是指向子节点的,如果有指向(也就是子节点存在),那么这两个节点之间是不是就有一个联系,而这个联系就是用left和right来表示的,所以说就是树的边。(解释的还可以把,自夸中)。
现在我们来想一下树有些什么操作,算了不想了,我给出了下面几种操作,不够的自行补充:(tip:我们现在写的树是根据二叉查找树BST来定义的)。
简单的解释一下BST的定义:
1.树中每个节点的子节点不允许超过两个(也就是二叉树的定于)
2.相对较小的值保存在左子节点中
3.相对较大的值保存在右子节点中
看有哪些骚操作:
增加节点
1.如果树中没有跟节点,那么插入的节点就是跟节点
2.如果有了树在插入之前有了根节点,就比较麻烦一点,且看怎么处理
2.1 设置当前节点为根节点。
2.2 如果新节点的值小于当前节点的值,则设置当前节点为原节点的左节点;反之,执行2.4
2.3. 如果当前节点左节点为null,那就把新节点插入到这个位置,退出循环;反之,继续执行下一次循环
2.4. 如果新节点的值大于当前节点的值,则设置当前节点为原节点的右节点;
2.5. 如果当前节点右节点为null,那就把新节点插入到这个位置,退出循环;反之,继续执行下一次循环
ok,有了这个思考过程,我们来写一下把,毕竟光说不练假把式:
// 树 class BST { constructor() { this.root = null; } // insert:插入节点函数 insert(data) { var node = new Node(data,null,null); if (this.root === null) { this.root = node; return; } var current = this.root; var parent; while (true) { parent = current; if (data < current.data) { current = current.left; if (current === null) { parent.left = node; break; } } else { current = current.right; if (current === null) { parent.right = node; break; } } } } }
看插入函数,算法一大推,实际代码还是很少的。
遍历节点
1. 中序遍历(按照节点上的值,以升序访问BST上所有的节点)
2. 先序遍历(先访问根节点,然后以同样的方式访问左子树和右子树)
3. 后序遍历(先访问叶子节点,从左子树到有子树,在到根节点)
不要问我为什么会存在这三种遍历方式,(解释起来很麻烦,百度看别人的反而更加容易理解)
我们来看看三种遍历方式的实现
class BST { constructor() { this.root = null; } // insert:插入节点函数 insert(data) { var node = new Node(data,null,null); if (this.root === null) { this.root = node; return; } var current = this.root; var parent; while (true) { parent = current; if (data < current.data) { current = current.left; if (current === null) { parent.left = node; break; } } else { current = current.right; if (current === null) { parent.right = node; break; } } } } // inOrder:中序遍历 inOrder(node) { if (node !== null) { this.inOrder(node.left); console.log(node.show()); this.inOrder(node.right); } } // preOrder:先序遍历 preOrder(node) { if (node !== null) { console.log(node.show()); this.preOrder(node.left); this.preOrder(node.right); } } // postOrder: 后序遍历 postOrder(node) { if (node !== null) { this.preOrder(node.left); this.preOrder(node.right); console.log(node.show()); } } }
我相信,睿智的你是不会被这个递归思想难倒的,我就不多bb了,我们来测试一下:
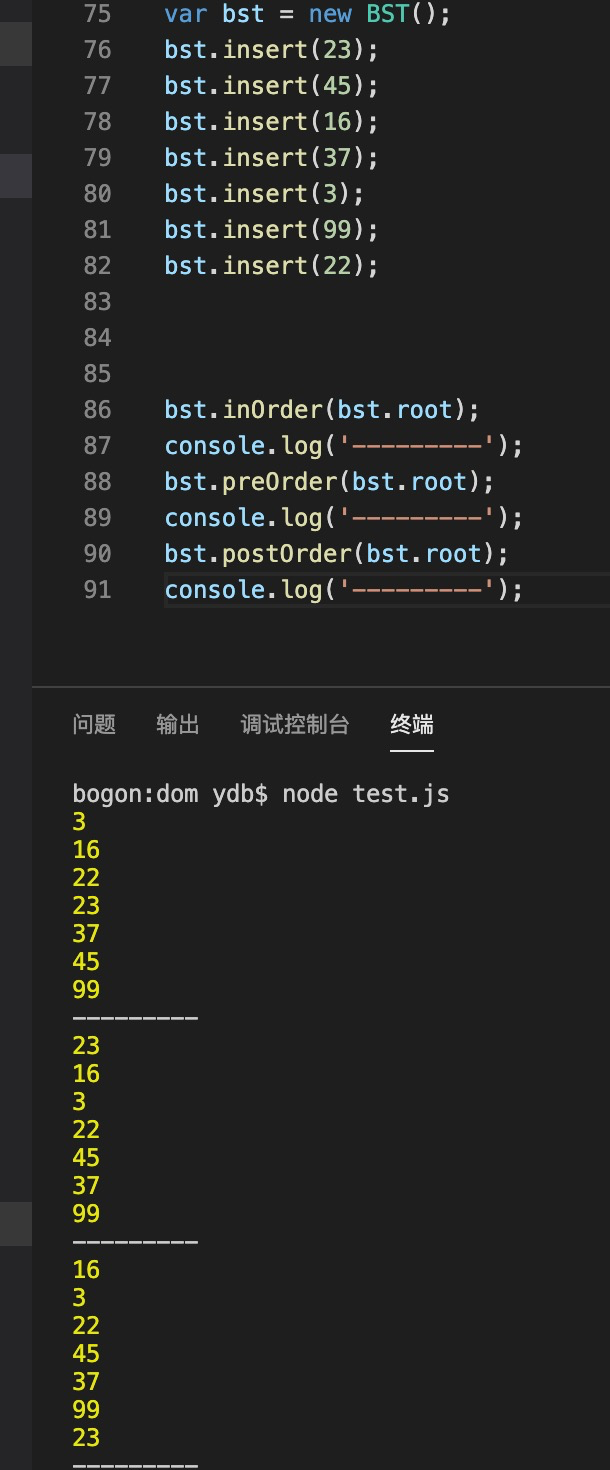
还行,没事看点黄色的东西。
查找操作
不知道你还记得我们插入节点的时候,有一个很巧妙的操作,那就是相对于较小的节点总是放在左边的,相对较大的节点总是放在右边的。有了这个特性,那么我们在二叉查找树中进行查找岂不是很简单。下面实现三种查找
1. 查找最大值
2.查找最小值
3.查找给定的值
代码如下:
// max:查找最大值 max() { var current = this.root; while (current.right !== null) { current = current.right; } return current.data; } // min:查找最小值 min() { var current = this.root; while (current.left !== null) { current = current.left; } return current.data; } // find:查找给定值 find(data) { var current = this.root; while (current !== null) { if (current.data === data) { return current; } else if (current.data < data) { current = current.right; } else { current = current.left } } return null }
老规矩,测试一下:

接下来就是删除节点操作了。
节点删除
其实节点删除是最复杂的操作,因为删除的节点不一样,对应的操作也不一样,树的构成不一样,那么操作也不一样。举个栗子,比如树只有一个根节点,那么就直接删除了,什么操作又不用进行。但是万一,该节点下面还有一个左节点或者右节点或者左右节点都存在了?所以我们要思考一下。
这里为了让大家弄明白删除的操作思考,我就照搬别人的解释了:
从BST中删除节点的第一步是判断当前节点是否包含待删除的节点,如果包含,则删除该节点;如果不包含,则比较当前节点上的数据和待删除数据的。如果待删除数据小于当前节点上的数据,则移至当前节点的左子节点继续操比较;如果待删除数据大于当前节点上的数据,则移至当前节点的右子节点继续比较。
如果待删除节点是叶子节点(没有子节点),那么只需要将父节点指向它的链接指向null,也就是删除当前边。
如果待删除节点只包含一个子节点,那么原本指向它的节点就要做一些调整,使其指向它的子节点。
如果待删除节点包含两个子节点,正确的做法有两种:要么查找待删除节点左子树上的最大值,要么就查找待删除节点右子树上的最小值。(这里我们选择第一种方法)
我们需要一个查找子树上最大值的方法,后面会用它的值创建一个临时节点,将临时节点上的值复制到待删除节点上,就完成了删除节点,然后删除这个临时节点。
为什么要这么操作:因为我们知道,二叉查找树的左边是相对较小的,右边是相对较大的(看insert方法或者定义),那么我们删除它的父节点,父节点删除了,它的子节点应该要保存下来,还是要构成二叉查找树的形态,所以只有左子树的最大值或者右子树上最小的值去替代父节点,才能继续维持这个结构(你说是不是,嘿嘿)
好了,bb一大推,我们来看一下代码怎么实现:
// remove:删除节点 remove(data) { this.root = this.removeNode(this.root,data); } //removeNode:实际操作删除的方法 removeNode(node,data) { if (node === null) { return null; } if (data === node.data) { // 没有子节点 if(node.left === null && node.right === null) { return null; } // 没有左节点 if (node.left === null) { return node.right; } // 没有右节点 if(node.right === null) { return node.left; } // 有两个节点 var tempNode = this.getMax(node.left); node.data = tempNode.data; node.left = this.removeNode(node.left,tempNode.data); return node; } else if (data < node.data) { node.left = this.removeNode(node.left,data); return node; } else { node.right = this.removeNode(node.right,data); return node; } } // getMax:获取左子树上的最大值 getMax(node) { var current = node; while (current.right !== null) { current = current.right; } return current.data; }
不得不承认,这段代码需要好好回味一下。
测试一下:

简直就是ojbk。
还坚持一下,我们在来看一个计数功能。
计数
BST的一个用途就是记录一组数据出现的次数,所以我们现在要修改一下新增函数,如果树中有该节点那么我们将其count加一,没有就直接插入节点。
看看代码:
// insert:插入节点函数 insert(data) { var node = new Node(data, null, null); if (this.root === null) { this.root = node; return; } var hasNode = this.find(data); if (hasNode) { // 更新计数 this.update(hasNode); return; } var current = this.root; var parent; while (true) { parent = current; if (data < current.data) { current = current.left; if (current === null) { parent.left = node; break; } } else { current = current.right; if (current === null) { parent.right = node; break; } } } } // update:更新节点计算 update(node){ node.count++; }
同时为了方便我们看结果,我修改了一下Node类的show方法:
// show:显示当前节点的值 show() { console.log(this.data+'出现了'+this.count+'次'); return this.data; }
测试一下: