KMP算法

　　KMP算法(3个人的名字的头字母，Knuth与Pratt和Morris)，主要就是应用有限自动机的原理。

　　KMP算法的核心思想是利用已经得到的部分匹配信息来进行后面的匹配过程。

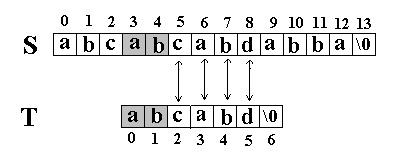
　　在S=”abcabcabdabba”中查找T=”abcabd”，如果使用KMP匹配算法，当第一次搜索到S[5] 和T[5]不等后，S下标不是回溯到1，T下标也不是回溯到开始，而是根据T中T[5]==’d’的模式函数值（next[5]=2），直接比较S[5] 和T[2]是否相等(换到状态2中去)，因为相等，S和T的下标同时增加。

　　

　　一. 模式值next[n]的计算，也就是状态转移

　　一定要想成状态转移，eg：  str数组为：  ababaa

a	-1
ab	-1
aba	0
abab	1
ababa	2
ababaa	0

　　next[n]的值也就是假如它的下一个错了，它可以回溯的状态(只能向上)。next[n]的下标代表状态。状态的增加最多加一(依赖字符的增加)。

　　*第一个状态只有一个可回溯的，那就是-1状态。

　　*当str[i]==str[j+1] (j为上一个状态可回溯的状态)，此时符合上一个状态的增加。所以next[i]=j+1。

　　*当str[i]!=str[j+1]，此时i状态不符合上一个状态的增加，所以反复回溯再上一个状态，直至i状态符合j状态的增加或者状态-1。

　　二. 字符串的匹配

　　失配后，回溯，和生成next的时候一样，反复回溯再上一个状态，直至成功或者状态-1。

　　相关解释在代码中

/**
 * KMP字符串匹配
 * @author jslee
 *
 */
public class kmp {

    public static void main(String[] args) {
        String str1 = "ababababbabababa";
        String str2 = "ababa";
        System.out.println(kmpMatch(str1,str2));
    }
    
    public static int[] calcuNext(String string){
        if (string == null) 
            return null;
        char[] str = string.toCharArray();
        int[] next = new int[str.length];
        int j;
        next[0] = -1;//第一个状态只有一个可回溯的，那就是-1状态
        for (int i = 1; i < next.length; i++) {
            j = next[i-1];  //上一个状态
            //上一个状态为-1时，不用再回溯
            //str[i]!=str[j+1] 需要往上回溯
            while (j>=0 && str[i]!=str[j+1]) {           
                j = next[j];
            }
            //符合上一个状态的增加
            if (str[i]==str[j+1])
                next[i] = j+1;
            //回溯后也不符合，那就只有原始状态-1了
            else
                next[i] = -1;  
        }
        return next;
    }
    public static int kmpMatch(String bigString, String string) {
        if (bigString == null && string == null) 
            return -1;
        int returnInt=0;  //返回的值，整体匹配成功的个数
        char[] bigStr = bigString.toCharArray();
        char[] str = string.toCharArray();
        int[] next = calcuNext(string);  //next状态数组
        int matchNum=0;    //字符匹配的个数
        for (int i = 0; i < bigStr.length; i++) { //遍历大数组
            if (bigStr[i] == str[matchNum]) { //字符匹配成功，下一个字符
                matchNum++;
            }else {//失配，反复回溯再上一个状态，直至成功或者状态-1。
                if (matchNum!=0) { //回溯
                    matchNum = next[matchNum-1]+1;
                    i--;     //！！一定要记住i不变，再次判断此字符
                }//matchNum为0时，不用回溯
            }
            if (matchNum == str.length) { //当整个匹配成功时，记录并回溯
                matchNum = next[matchNum-1]+1;
                returnInt++;
            }
        }
        return returnInt;
    }
}

 　　三.变种算法

　　1.求字符串的最短循环节，对于每个i，求一个最大的整数K，使得字符串的前i个字符组成的前缀是某个字符子串重复K次得到。输出i和K

　　eg：aabaabaabaab     ->   i=2,6,9,12 时，K为 2，2，3，4

public static void main(String[] args) {
    String str1 = "aabaabaabaab";
    int[] next = calcuNext(str1);
    for (int i = 0; i < next.length; i++) {
        //此处i-next[i] = (i+1)(当前位置) - (next[i]+1)(回溯的位置)
        //当前位置 如果是 当前位置和回溯的位置之差 的倍数 那就代表这个“错位”刚好是一个循环节
        if(next[i]!=-1 && (i+1)%(i-next[i])==0) 
            System.out.println("数组下标为"+i+"  找到了,K值为："+(i+1)/(i-next[i]));
    }
}