算法学习记录-排序——归并排序

归并排序

　　利用了完全二叉树的堆排序在效率上提高了不少。但是堆排序主要耗费时间在调整堆上，算法效率也不够稳定。

对于二叉树的应用，还有没有其他方法能够保持算法的效率，也能够使其是一个稳定的算法。（堆排序不够稳定）

具体效率可以查看《算法导论》、《数据结构与算法》（严蔚敏）

　　想想二叉树的结构，如果我们比较两个数，我们想想将两个树作为叶子，比较结果存放在根中。

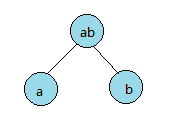
如果是四个数呢？

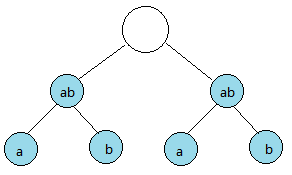四个数分别为四个叶子，通过两两比较形成一个小集合，然后小集合再比较最后形成最终的结果。

这就是归并的思想。开始不理解为什么叫归并，后来看到有人写过：

先递归分解，再合并成数组

归并算法用了 分治法（Divide and Conquer）的一个非常典型的应用。值得注意的是归并排序是一种稳定的排序方法。（算法比较稳定）

 

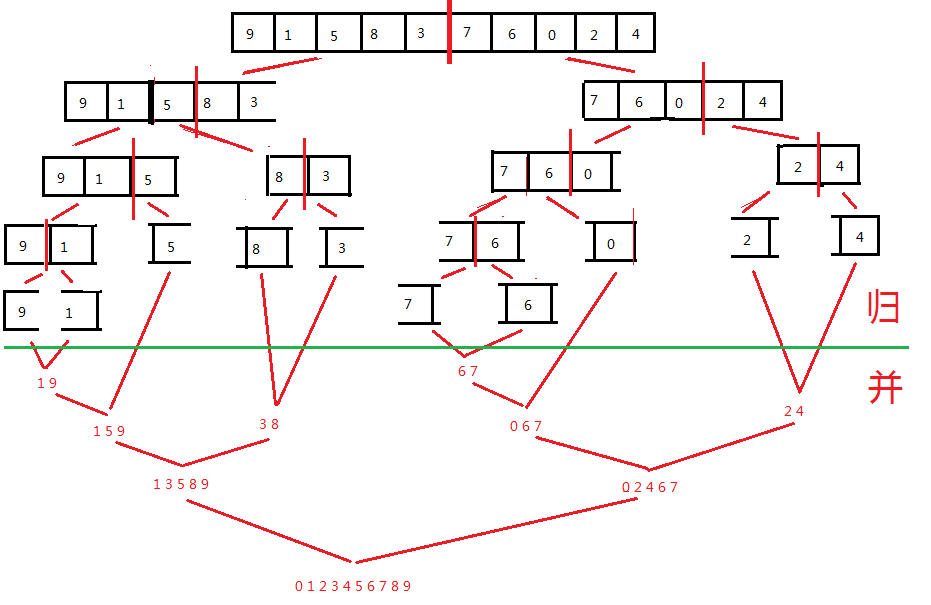
理解了，代码就好写了。

两个关键：

分解数组mergeDiv

合并数组mergeIn

看上图分解，我们以左边 9 1为例，最终分解为 9  和 1结点后再开始排序，

mergeDiv（左） 得到的起始序号是0，终止序号是0，得到实际的数==> 9

mergeDiv（右） 得到的起始序号是1，终止序号是1，得到实际的数==> 1

mergeIn（左右）排序，返回==> 1 9

想想在二叉树一章，这有点像后续遍历。

对于 19 5

mergeDiv（左） 得到的起始序号是0，终止序号是1，得到实际序列==>1 9(之前已经排好了)

mergeDiv（右） 得到的起始序号是2，终止序号是2，得到实际序列==>2

mergeIn(左右)  对上面两个序列 起始0，中间1，终止2 返回  ==>1 2 9 

依次类推。。。

代码：

void mergeIn(myDataType *ary,int s,int m,int e)
{
    int i,j;
    int len1 = (m-s)+1;
    int len2 = e-m;

    myDataType *list1 = (myDataType *)malloc(sizeof(myDataType)*len1);
    myDataType *list2 = (myDataType *)malloc(sizeof(myDataType)*len2);
    
    for (i=0;i<len1;i++)
    {
        list1[i] = ary[s+i];
    }

    for (i=0;i<len2;i++)
    {
        list2[i] = ary[m+1+i];
    }

    i=0;
    j=0;
    while(i < len1 && j < len2)
    {
        if (list1[i] >= list2[j])
        {
            ary[s+i+j] = list2[j];
            j++;
        }
        else
        {
            ary[s+i+j] = list1[i];
            i++;
        }
    }
    while(i<len1)
    {
        ary[s+i+j] = list1[i];
        i++;
    }
    while(j<len2)
    {
        ary[s+i+j] = list2[j];
        j++;
    }

}

void mergeDiv(myDataType *ary,int sIdx,int eIdx)
{
    if (sIdx >= eIdx)
    {
        return ;
    }
    int mid = (sIdx+eIdx)/2;

    mergeDiv(ary,sIdx,mid);
    mergeDiv(ary,mid+1,eIdx);
    //printf("s=%d,mid=%d,e=%d
",sIdx,mid,eIdx);
    mergeIn(ary,sIdx,mid,eIdx);
}



void mergeSort(myDataType *ary,int len)
{
    mergeDiv(ary,0,len-1);
}

按照之前那幅图，绘制了一个函数间调用关系

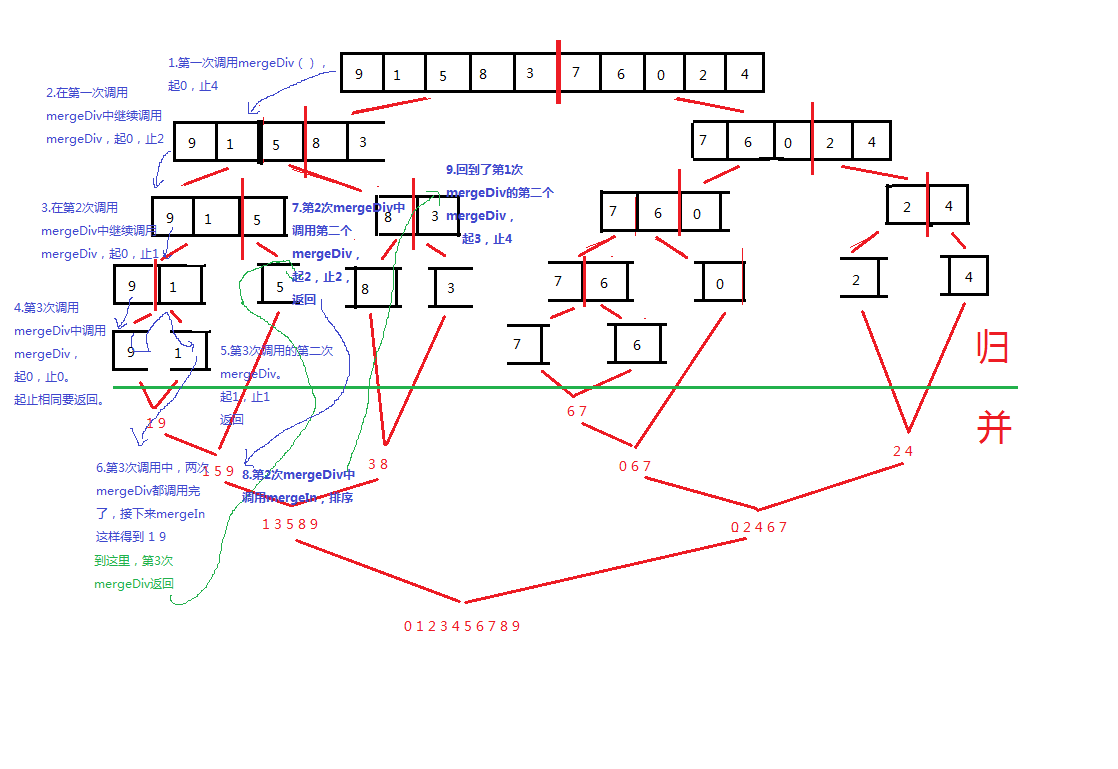
这里写到了9，后面基本一样。排完左子树，再排右子树，最终返回后，调用mergeIn，完成左右子树排序。

完整代码：

#include "stdlib.h"

typedef int myDataType;
myDataType src_ary[10] = {9,1,5,8,3,7,6,0,2,4};
//myDataType src_ary[10] = {1,2,3,4,5,6,7,8,9,10};
//myDataType src_ary[10] = {10,9,8,7,6,5,4,3,2,1};
void prt_ary(myDataType *ary,int len)
{
    int i=0;
    while(i < len)
    {
        printf(" %d ",ary[i++]);
    }
    printf("
");
}

void mergeIn(myDataType *ary,int s,int m,int e)
{
    int i,j;
    //获取两个序列长度
    int len1 = (m-s)+1;
    int len2 = e-m;
    
    //开辟新空间，为排序做准备。
    myDataType *list1 = (myDataType *)malloc(sizeof(myDataType)*len1);
    myDataType *list2 = (myDataType *)malloc(sizeof(myDataType)*len2);
    
    //准备两个待比较序列数据
    for (i=0;i<len1;i++)
    {
        list1[i] = ary[s+i];
    }

    for (i=0;i<len2;i++)
    {
        list2[i] = ary[m+1+i];
    }

    //比较，因为用来其他空间来存放数据，最后比较后的数据直接给原数据
    i=0;
    j=0;
    while(i < len1 && j < len2)
    {
        if (list1[i] >= list2[j])
        {
            ary[s+i+j] = list2[j];
            j++;
        }
        else
        {
            ary[s+i+j] = list1[i];
            i++;
        }
    }
    while(i<len1)
    {
        ary[s+i+j] = list1[i];
        i++;
    }
    while(j<len2)
    {
        ary[s+i+j] = list2[j];
        j++;
    }

}

void mergeDiv(myDataType *ary,int sIdx,int eIdx)
{
    if (sIdx >= eIdx)
    {
        return ;
    }
    int mid = (sIdx+eIdx)/2;

    mergeDiv(ary,sIdx,mid);
    mergeDiv(ary,mid+1,eIdx);
    printf("s=%d,mid=%d,e=%d
",sIdx,mid,eIdx);
    mergeIn(ary,sIdx,mid,eIdx);
}



void mergeSort(myDataType *ary,int len)
{
    mergeDiv(ary,0,len-1);
}

int _tmain(int argc, _TCHAR* argv[])
{
    printf("before sort:
");
    prt_ary(src_ary,10);

    //bubble_sort(src_ary,10);
    //bubble_sort_modify1(src_ary,10);
    //bubble_sort_opt(src_ary,10);
    //selectionSort(src_ary,10);
    //insertionSort(src_ary,10);
    //shellSort(src_ary,10);
    //heapSort(src_ary,10);
    mergeSort(src_ary,10);
    printf("after sort:
");
    prt_ary(src_ary,10);



    getchar();
    return 0;
}

归并排序用了其他内存空间，是一个耗费空间排序，但是其稳定性高。

结果：

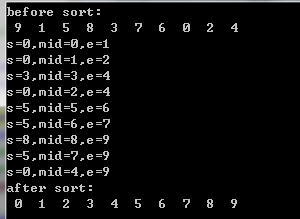
中间的就是 每次访问时候的序号。