之前我们介绍过,在一个工程中我们关心两个问题:
(1)工程是否顺利进行
(2)整个工程最短时间。
之前我们优先关心的是顶点(AOV),同样我们也可以优先关心边(同理有AOE)。(Activity On Edge Network)
看看百度百科上解释:
AOE网:Activity on edge network
若在带权的有向图中,以顶点表示事件,以有向边表示活动,边上的权值表示活动的开销(如该活动持续的时间),则此带权的有向图称为AOE网。
如果用AOE网来表示一项工程,那么,仅仅考虑各个子工程之间的优先关系还不够,更多的是关心整个工程完成的最短时间是多少;
哪些活动的延期将会影响整个工程的进度,而加速这些活动是否会提高整个工程的效率。
因此,通常在AOE网中列出完成预定工程计划所需要进行的活动,每个活动计划完成的时间,要发生哪些事件以及这些事件与活动之间的关系,
从而可以确定该项工程是否可行,估算工程完成的时间以及确定哪些活动是影响工程进度的关键。
很显然,顶点表示事件,边表示活动,边的权则表示活动持续时间。
AOE一般用来估算工程的完成时间。
AOE表示工程的流程,把没有入边的称为始点或者源点,没有出边的顶点称为终点或者汇点。一般情况下,工程只有一个开始,一个结束,
所以正常情况下,AOE只有一个源点一个汇点。
AOV和AOE的区别:
1.AOV用顶点表示活动的网,描述活动之间的制约关系。
2.AOE用边表示活动的网,边上的权值表示活动持续的时间。
AOE 是建立在子过程之间的制约关系没有矛盾的基础之上,再来分析整个过程需要的时间。
AOE研究:
a.完成整个过程至少需要多长时间。
b.哪些活动影响工程的进度?
关键路径:从源点到汇点具有最大长度的路径。这个概念要清楚,一个工程不一定有一条关键路径,可能会有多条。
关键活动:关键路径上的活动(边)。
针对上面AOE所关心的问题,要想缩短工程时间,就缩短关键路径上的过程即可。(缩短后可能出现之前的关键路径变成了非关键路径)
由于AOE网上所有的活动是可以并行进行。这里举一个例子,组装一个变形金刚,需要头,左膀右臂,身体,左腿右腿。
我们可以有两种方法:1.先做好头,做左手臂,做右手臂,做身体,做左腿,做右腿,然后再组装。
2.同时做头、手臂、身体、腿的部分,每有一个头、两个手臂、两个腿和一个身体的时候,就可以组装了。
方法1.如我们计算机中的串行运行。这样时间开销是累加的。
方法2.如我们计算机中的并行运行。这样时间开销可以立体应用。在此方法中,同时做各个部位时间不同,比如做头时间最长,那么整个一个
变形金刚所用的时间决定与做头的时间,如果做手臂的时间是做头时间的一半,那么就是说做手臂的时间点可以在头做了一半的时候。只要不超过这个
时间点,手臂部分是不会影响整个工程的进度的。
这里定义四个定义:前两个针对顶点,后两个针对边
事件最早开始时间:顶点Vi最早发生的时间。
事件最晚开始时间:顶点Vi最晚发生的时间,超出则会延误整个工期。
活动的最早开始时间:边Eg最早发生时间。
活动的最晚开始时间:边Eg最晚发生时间。不推迟工期的最晚开工时间。
下面这个例子说明一下:
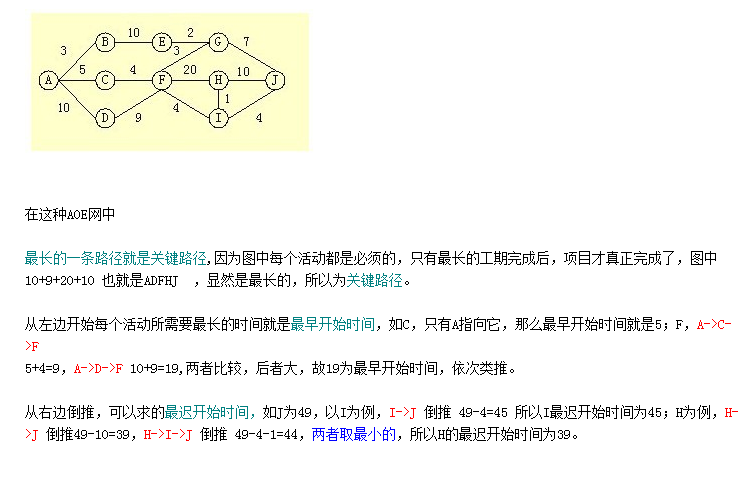
说明:上图中J中为49,是最早开始时间。这里可以看到最早开始时间,就是完要成该顶点,前面的所有到该点的路径都要已经完成。所以取路径最大那一条。
补充说明:
事件最早开始时间:例子图中,F点,ACF(9) 和 ADF(19),到达F点时候,保证AC和AD都完成,这样 F才能开始,所以F点的最早开始时间取最大值,即19.
可以看出,要求出到某一点的最早开始时间,则需要将汇于该点的所有路径的时间求出来,取最大值。
事件最迟开始时间:这里是反着推,比如H点最迟开始时间,H到J 与 H到I到J两条路径,39 和 44,所谓最迟开始时间,就是超过这个时间就会影响整个工程进度,
而这个时间是时间点,是从源点工程开始计时的,所以对于H点,39和44是相对于源点,如果取44,则H-J这条路径就会拖延,最迟开始时间选择最小值。
关键路径的特点:我们寻找关键路径——关键路径就是关键活动(顶点与顶点之间的边组成),就是我们怎么判断该顶点是否为关键活动(边)的顶点,即判断边是否为关键活动。
前面定义过,关键路径就是图中从源点到汇点最长(权值最大)的路径。
这条路径就决定了整个工程的工期,这说明一个什么问题?
关键路径上的顶点与顶点之间的活动的应该最早开始和最迟开始时间是相等的,
如果不等那么说明活动还有余额时间(在最早开始时间和最迟开始时间之间可以任选一个时间点开始),这说明还有其他活动是决定这个工程时间的,那就不是关键路径了。
算法思想:
要准备两个数组,a:最早开始时间数组etv,b:最迟开始时间数组。(针对顶点即事件而言)
1.从源点V0出发,令etv[0](源点)=0,按拓扑有序求其余各顶点的最早发生时间etv[i](1 ≤ i ≤ n-1)。同时按照上一章
拓扑排序的方法检测是否有环存在。
2.从汇点Vn出发,令ltv[n-1] = etv[n-1],按拓扑排序求各个其余各顶点的最迟发生时间ltv[i](n-2 ≥ i ≥ 2);
3.根据各顶点的etv和ltv数组的值,求出弧(活动)的最早开工时间和最迟开工时间,求每条弧的最早开工时间和最迟开工时间是否相等,若相等,则是关键活动。
注意:1,2 完成点(事件)的最早和最迟。3根据事件来计算活动最早和最迟,从而求的该弧(活动)是否为关键活动。
关键代码:
1.对图进行拓扑排序,存储了拓扑排序的顺序,作为关键路径的计算最迟开始时间的依据。
1 int TopplogicalSort(GraphAdjList *g) 2 { 3 int count=0; 4 eNode *e=NULL; 5 6 StackType *stack=NULL; 7 StackType top=0; 8 stack = (StackType *)malloc((*g).numVextexs*sizeof(StackType)); 9 10 int i; 11 12 //初始化拓扑序列栈 13 g_topOfStk = 0; 14 //开辟拓扑序列栈对应的最早开始时间数组 15 g_etv = (int *)malloc((*g).numVextexs*sizeof(int)); 16 //初始化数组 17 for (i=0;i<(*g).numVextexs;i++) 18 { 19 g_etv[i]=0; 20 } 21 //开辟拓扑序列的顶点数组栈 22 g_StkAfterTop = (int *)malloc(sizeof(int)*(*g).numVextexs); 23 24 25 26 27 for (i=0;i<(*g).numVextexs;i++) 28 { 29 if (!(*g).adjList[i].numIn) 30 { 31 stack[++top] = i; 32 // printf("init no In is %c\n",g_init_vexs[i]); 33 } 34 } 35 36 37 while(top) 38 { 39 int geter = stack[top]; 40 top--; 41 42 //把拓扑序列保存到拓扑序列栈,为后面做准备 43 g_StkAfterTop[g_topOfStk++] = geter; 44 45 printf("%c -> ",g_init_vexs[(*g).adjList[geter].idx]); 46 count++; 47 48 //获取当前点出度的点,对出度的点的入度减一(当前点要出图)。 49 //获取当前顶点的出度点表 50 e = (*g).adjList[geter].fitstedge; 51 while(e) 52 { 53 int eIdx = e->idx; 54 //选取的出度点的入度减一 55 int crntIN = --(*g).adjList[eIdx].numIn; 56 if (crntIN == 0) 57 { 58 //如果为0,则说明该顶点没有入度了,是下一轮的输出点。 59 stack[++top] = eIdx; 60 // printf("running the vex is %c\n",g_init_vexs[e->idx]); 61 } 62 63 //求出关键路径 64 if ((g_etv[geter] + e->weigh) > g_etv[eIdx]) 65 { 66 g_etv[eIdx] = g_etv[geter] + e->weigh; 67 } 68 69 e = e->next; 70 } 71 } 72 if (count < (*g).numVextexs)//如果图本身就是一个大环,或者图中含有环,这样有环的顶点不会进栈而被打印出来。 73 { 74 return false; 75 } 76 else 77 { 78 printf("finish\n"); 79 return true; 80 } 81 82 }
2.关键路径代码:
1 void CriticalPath(GraphAdjList g) 2 { 3 int i; 4 int geter; 5 eNode *e = NULL; 6 g_topOfStk--; 7 //1.初始化最迟开始时间数组(汇点的最早开始时间(初值)) 8 g_ltv = (int *)malloc(sizeof(int)*g.numVextexs); 9 for (i=0;i<g.numVextexs;i++) 10 { 11 g_ltv[i] = g_etv[g.numVextexs-1]; 12 } 13 14 //2.求每个点的最迟开始时间,从汇点到源点推。 15 while (g_topOfStk) 16 { 17 //获取当前出栈(反序)的序号 18 geter = g_StkAfterTop[g_topOfStk--]; 19 //对每个出度点 20 if (g.adjList[geter].fitstedge != NULL) 21 { 22 e = g.adjList[geter].fitstedge; 23 while(e != NULL) 24 { 25 int eIdx = e->idx; 26 if (g_ltv[eIdx] - e->weigh < g_ltv[geter]) 27 { 28 g_ltv[geter] = g_ltv[eIdx] - e->weigh; 29 } 30 e = e->next; 31 } 32 } 33 } 34 35 int ete,lte;//活动最早开始和最迟开始时间 36 37 38 39 printf("start:->"); 40 //3.求关键活动,即ltv和etv相等的 41 for (i=0;i<g.numVextexs;i++) 42 { 43 if (g.adjList[i].fitstedge) 44 { 45 e = g.adjList[i].fitstedge; 46 while(e) 47 { 48 int eIdx = e->idx; 49 //活动(i->eIdx)最早开始时间:事件(顶点) i最早开始时间 50 ete = g_etv[i]; 51 //活动(i->eIdx)最迟开始时间:事件(顶点) eIdx 最迟开始时间 减去 活动持续时间 52 lte = g_ltv[eIdx] - e->weigh; 53 if (ete == lte) 54 { 55 printf("(%c - %c)->",g_init_vexs[i],g_init_vexs[eIdx]); 56 } 57 e= e->next; 58 } 59 } 60 } 61 printf(" end\n"); 62 }
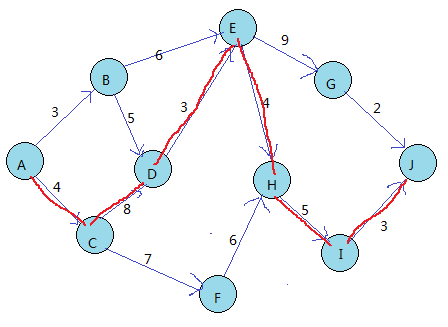
编程所用的图:
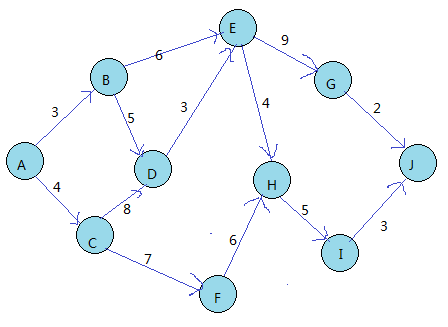
拓扑排序结果:

过程:
1.从J开始,无后继,不做任何事情;
2.G,G的ltv为27,ltv-weight = 27-2 < 27,所以G的ltv为25;
3.I,I的ltv为27,ltv-weight = 27 -3 < 27,所以I的ltv为24;
4.H,H的ltv为24(I的ltv),24-5 < 24,所以H 的ltv为19;
依次类推。。。
完成top排序和关键路径后:
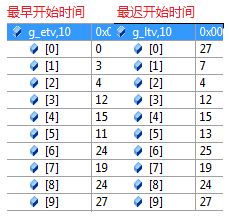
全局存放各个顶点的最早开始和最迟开始时间:
完整代码:
1 // grp-top.cpp : 定义控制台应用程序的入口点。 2 // 3 // grp-top.cpp : 定义控制台应用程序的入口点。 4 // 5 6 #include "stdafx.h" 7 #include <stdlib.h> 8 9 10 #define MAXVEX 100 11 #define IFY 65535 12 13 14 typedef char VertexType; 15 typedef int EdgeType; 16 typedef int IdxType; 17 typedef int QueueType; 18 typedef int StackType; 19 20 21 //------- 22 int *g_etv = NULL; 23 int *g_ltv = NULL; 24 int *g_StkAfterTop; 25 int g_topOfStk; 26 27 28 ///--------------------------------------- 29 //边节点 30 typedef struct EdgeNode{ 31 IdxType idx; 32 int weigh; 33 struct EdgeNode* next; 34 }eNode; 35 36 //顶点节点 37 typedef struct VexNode{ 38 int numIn; //入度数量 39 IdxType idx; 40 eNode *fitstedge; 41 }vNode; 42 43 //图的集合:包含了一个顶点数组 44 typedef struct { 45 vNode adjList[MAXVEX]; 46 int numVextexs,numEdges; 47 }GraphAdjList; 48 49 ///----------------------------------- 50 /*VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I','J','K','L'}; 51 52 char *g_input[] = { 53 "A->B->C->D", 54 "B->E", 55 "C->F->I->J", 56 "D->E->I->J", 57 "E", 58 "F->K", 59 "G->F->H->K", 60 "H->I", 61 "I->J->L", 62 "J->E->K", 63 "K->L", 64 "L" 65 };*/ 66 67 ///----------------------------------- 68 VertexType g_init_vexs[MAXVEX] = {'A','B','C','D','E','F','G','H','I','J'}; 69 70 char *g_input[] = { 71 "A->B->C", 72 "B->D->E", 73 "C->D->F", 74 "D->E", 75 "E->G->H", 76 "F->H", 77 "G->J", 78 "H->I", 79 "I->J", 80 "J", 81 NULL 82 }; 83 84 char *g_input_weigh[] = { 85 "3,4",//A 86 "5,6",//B 87 "8,7",//C 88 "3",//D 89 "9,4",//E 90 "6",//F 91 "2",//G 92 "5",//H 93 "3",//I 94 " ",//J 95 NULL 96 }; 97 //=============================================================== 98 //队列 99 100 //队列节点 101 typedef struct Node { 102 QueueType data; 103 struct Node *next; 104 }QNode,*qQNode; 105 106 //队列指示 107 typedef struct { 108 int length; 109 qQNode frnt,rear; 110 }spQueue; 111 112 void init_Queue(spQueue *Q) 113 { 114 (*Q).frnt = NULL; 115 (*Q).rear = NULL; 116 (*Q).length = 0; 117 } 118 bool isEmptyQueue(spQueue Q) 119 { 120 if (Q.length == 0) 121 { 122 return true; 123 } 124 return false; 125 } 126 //进队 127 void unshiftQueue(spQueue *Q,QueueType elem) 128 { 129 //队列空 130 if (isEmptyQueue(*Q)) 131 { 132 qQNode n = (qQNode)malloc(sizeof(QNode)); 133 n->data = elem; 134 n->next = NULL; 135 136 (*Q).frnt = n; 137 (*Q).rear = n; 138 (*Q).length = 1; 139 } 140 else 141 { 142 qQNode n = (qQNode)malloc(sizeof(QNode)); 143 n->data = elem; 144 n->next = NULL; 145 146 (*Q).rear->next = n; 147 148 (*Q).rear = n; 149 (*Q).length++; 150 } 151 } 152 153 //出队 154 QueueType shiftQueue(spQueue *Q) 155 { 156 if (isEmptyQueue(*Q)) 157 { 158 printf("Warning:Queue is empty!!!\n"); 159 return NULL; 160 } 161 if ((*Q).length == 1) 162 { 163 QueueType sh = (*Q).frnt->data; 164 (*Q).frnt = NULL; 165 (*Q).rear = NULL; 166 (*Q).length = 0; 167 return sh; 168 } 169 QueueType sh = (*Q).frnt->data; 170 (*Q).frnt = (*Q).frnt->next; 171 (*Q).length--; 172 173 return sh; 174 } 175 176 //打印队列 177 void prt_que(spQueue que) 178 { 179 if (isEmptyQueue(que)) 180 { 181 return ; 182 } 183 qQNode pos = que.frnt; 184 while(que.rear->next != pos && pos != NULL) 185 { 186 printf(" %d ",pos->data); 187 pos = pos->next; 188 } 189 printf("\n"); 190 } 191 //=============================================================== 192 193 ///------- 194 //由节点找节点的序号 195 IdxType strFindIdx(char ch) 196 { 197 int i=0; 198 VertexType *p = g_init_vexs; 199 while(p != NULL) 200 { 201 if(*p == ch) 202 { 203 return i; 204 } 205 p++; 206 i++; 207 } 208 return i; 209 } 210 211 //由序号找节点 212 VertexType idxFindStr(IdxType i) 213 { 214 return g_init_vexs[i]; 215 } 216 217 void prt_strings(char *p) 218 { 219 char *pos = p; 220 while (NULL != *pos) 221 { 222 printf("%c",*pos); 223 pos++; 224 } 225 printf("\n"); 226 } 227 228 void prt_strArrays(char *p[],int num) 229 { 230 char **pos = p; 231 int i=0; 232 while( *pos != NULL && i < num) 233 { 234 prt_strings(*pos); 235 pos++; 236 i++; 237 } 238 } 239 240 //自己规定:顶点只能是大写。 241 bool isVexter(char p) 242 { 243 if (p>='A' && p<='Z') 244 { 245 return true; 246 } 247 return false; 248 } 249 250 bool isNumeric(char p) 251 { 252 if (p >= '0' && p <= '9') 253 { 254 return true; 255 } 256 return false; 257 } 258 259 void init_GrapAdjList(GraphAdjList *g,char **str,char **wstr) 260 { 261 char **pos = str; 262 263 int cnt=0; 264 int vcnt = 0; 265 char **wpos = wstr;//weight value 266 267 //入度清零 268 int i; 269 for (i=0;i<MAXVEX;i++) 270 { 271 (*g).adjList[i].numIn = 0; 272 } 273 274 while (*pos != NULL) //g_input的每行的首指针 275 { 276 int i=0; 277 while(**pos != NULL) //g_input的每行字母 278 { 279 if(isVexter(**pos)) //判断是否为顶点(我规定‘A’-‘Z’之间为顶点标志) 280 { 281 if (i == 0) //建立顶点的节点 282 { 283 (*g).adjList[cnt].idx = strFindIdx(**pos); 284 (*g).adjList[cnt].fitstedge = NULL; 285 286 i=1; 287 } 288 else if(i == 1) //建立第一个边的节点 289 { 290 eNode* n = (eNode*)malloc(sizeof(eNode)); 291 n->idx = strFindIdx(**pos); 292 n->next = NULL; 293 294 //weight 295 while (!isNumeric(**wpos)) 296 { 297 (*wpos)++; 298 } 299 n->weigh = **wpos-'0'; 300 (*wpos)++; 301 302 (*g).adjList[cnt].fitstedge = n; 303 i=2; 304 305 //添加入度 306 int iidx = strFindIdx(**pos); 307 (*g).adjList[iidx].numIn++; 308 } 309 else //边节点连接到前一个边节点上 310 { 311 eNode* n = (eNode*)malloc(sizeof(eNode)); 312 n->idx = strFindIdx(**pos); 313 n->next = NULL; 314 315 //weight 316 while (!isNumeric(**wpos)) 317 { 318 (*wpos)++; 319 } 320 n->weigh = **wpos-'0'; 321 (*wpos)++; 322 323 //first splist 324 eNode *r = (*g).adjList[cnt].fitstedge; 325 while (r->next != NULL) 326 { 327 r = r->next; 328 } 329 r->next = n; 330 331 //添加入度 332 int iidx = strFindIdx(**pos); 333 (*g).adjList[iidx].numIn++; 334 } 335 } 336 (*pos)++; 337 } 338 339 wpos++; 340 cnt++; 341 pos++; 342 343 } 344 (*g).numVextexs = cnt; 345 } 346 347 int TopplogicalSort(GraphAdjList *g) 348 { 349 int count=0; 350 eNode *e=NULL; 351 352 StackType *stack=NULL; 353 StackType top=0; 354 stack = (StackType *)malloc((*g).numVextexs*sizeof(StackType)); 355 356 int i; 357 358 //初始化拓扑序列栈 359 g_topOfStk = 0; 360 //开辟拓扑序列栈对应的最早开始时间数组 361 g_etv = (int *)malloc((*g).numVextexs*sizeof(int)); 362 //初始化数组 363 for (i=0;i<(*g).numVextexs;i++) 364 { 365 g_etv[i]=0; 366 } 367 //开辟拓扑序列的顶点数组栈 368 g_StkAfterTop = (int *)malloc(sizeof(int)*(*g).numVextexs); 369 370 371 372 373 for (i=0;i<(*g).numVextexs;i++) 374 { 375 if (!(*g).adjList[i].numIn) 376 { 377 stack[++top] = i; 378 // printf("init no In is %c\n",g_init_vexs[i]); 379 } 380 } 381 382 383 while(top) 384 { 385 int geter = stack[top]; 386 top--; 387 388 //把拓扑序列保存到拓扑序列栈,为后面做准备 389 g_StkAfterTop[g_topOfStk++] = geter; 390 391 printf("%c -> ",g_init_vexs[(*g).adjList[geter].idx]); 392 count++; 393 394 //获取当前点出度的点,对出度的点的入度减一(当前点要出图)。 395 //获取当前顶点的出度点表 396 e = (*g).adjList[geter].fitstedge; 397 while(e) 398 { 399 int eIdx = e->idx; 400 //选取的出度点的入度减一 401 int crntIN = --(*g).adjList[eIdx].numIn; 402 if (crntIN == 0) 403 { 404 //如果为0,则说明该顶点没有入度了,是下一轮的输出点。 405 stack[++top] = eIdx; 406 // printf("running the vex is %c\n",g_init_vexs[e->idx]); 407 } 408 409 //求出关键路径 410 if ((g_etv[geter] + e->weigh) > g_etv[eIdx]) 411 { 412 g_etv[eIdx] = g_etv[geter] + e->weigh; 413 } 414 415 e = e->next; 416 } 417 } 418 if (count < (*g).numVextexs)//如果图本身就是一个大环,或者图中含有环,这样有环的顶点不会进栈而被打印出来。 419 { 420 return false; 421 } 422 else 423 { 424 printf("finish\n"); 425 return true; 426 } 427 428 } 429 void CriticalPath(GraphAdjList g) 430 { 431 int i; 432 int geter; 433 eNode *e = NULL; 434 g_topOfStk--; 435 //1.初始化最迟开始时间数组(汇点的最早开始时间(初值)) 436 g_ltv = (int *)malloc(sizeof(int)*g.numVextexs); 437 for (i=0;i<g.numVextexs;i++) 438 { 439 g_ltv[i] = g_etv[g.numVextexs-1]; 440 } 441 442 //2.求每个点的最迟开始时间,从汇点到源点推。 443 while (g_topOfStk) 444 { 445 //获取当前出栈(反序)的序号 446 geter = g_StkAfterTop[g_topOfStk--]; 447 //对每个出度点 448 if (g.adjList[geter].fitstedge != NULL) 449 { 450 e = g.adjList[geter].fitstedge; 451 while(e != NULL) 452 { 453 int eIdx = e->idx; 454 if (g_ltv[eIdx] - e->weigh < g_ltv[geter]) 455 { 456 g_ltv[geter] = g_ltv[eIdx] - e->weigh; 457 } 458 e = e->next; 459 } 460 } 461 } 462 463 int ete,lte;//活动最早开始和最迟开始时间 464 465 466 467 printf("start:->"); 468 //3.求关键活动,即ltv和etv相等的 469 for (i=0;i<g.numVextexs;i++) 470 { 471 if (g.adjList[i].fitstedge) 472 { 473 e = g.adjList[i].fitstedge; 474 while(e) 475 { 476 int eIdx = e->idx; 477 //活动(i->eIdx)最早开始时间:事件(顶点) i最早开始时间 478 ete = g_etv[i]; 479 //活动(i->eIdx)最迟开始时间:事件(顶点) eIdx 最迟开始时间 减去 活动持续时间 480 lte = g_ltv[eIdx] - e->weigh; 481 if (ete == lte) 482 { 483 printf("(%c - %c)->",g_init_vexs[i],g_init_vexs[eIdx]); 484 } 485 e= e->next; 486 } 487 } 488 } 489 printf(" end\n"); 490 } 491 492 493 int _tmain(int argc, _TCHAR* argv[]) 494 { 495 GraphAdjList grp; 496 printf("print Matix: of Vextexs:\n"); 497 prt_strArrays(g_input,10); 498 printf("print Matix: of Weigh:\n"); 499 prt_strArrays(g_input_weigh,10); 500 501 init_GrapAdjList(&grp,g_input,g_input_weigh); 502 printf("Top sort:\n"); 503 if (!TopplogicalSort(&grp)) 504 { 505 printf("grp wrong!\n"); 506 } 507 508 CriticalPath(grp); 509 510 getchar(); 511 return 0; 512 }
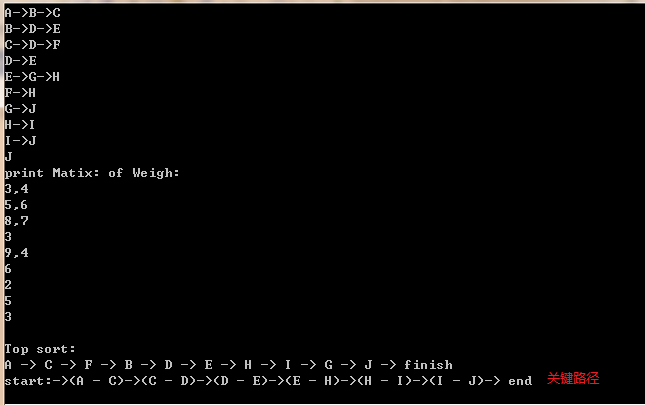
测试结果: