二叉树的结构中可以看到,会有许多空指针,这有浪费了资源。n个节点的二叉树共有n-1条分支。(除了根没有分支)
对于这样的结构: | left-child | data | right-child |,总分支指针(2n),空闲指针有(2n-(n-1))=n+1个分支。
能不能利用空闲指针呢?
通过利用这些空闲指针,方便我们索引这颗二叉树呢?
比如我们找到了头,就能够通过头节点的孩子节点和线索索引来访问整颗树,这有就没有必要像上篇文章那样,通过递归的调用 前序/中序/后序遍历整棵树。
这里注意:
线索化二叉树实质上通过一种遍历方式,将空闲指针指向该遍历方法下一个要访问的节点。即节约了空间,也提高了某些操作的效率。这种方法只需要遍历一次,就能够将
该树线索,以后只要通过头节点就能访问整棵树。
通过空闲指针来设置该节点的前驱和后驱,这有能够方便来索引整颗二叉树。
左边指针 ===》 前驱
右边右边 ===》后继
通过这样的修改能够充分利用这样的结构。
更加优化下:有如下结构
| left-child | left-flag | data | right-flag | right-child |
child = 指向孩子的节点的指针。
flag = 标记该child是孩子指针还是 前驱/后继的指针。
如下一棵树:
要将他线索化,可以按照前序/中序/后序等方式线索化它。下面我们将按照中序遍历方式线索化它。
原图:
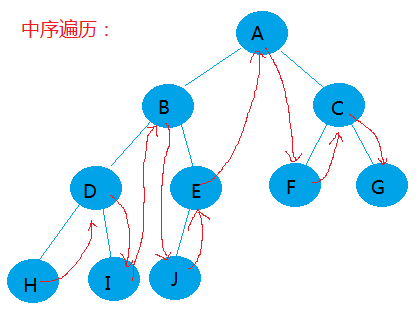
线索化后的图:
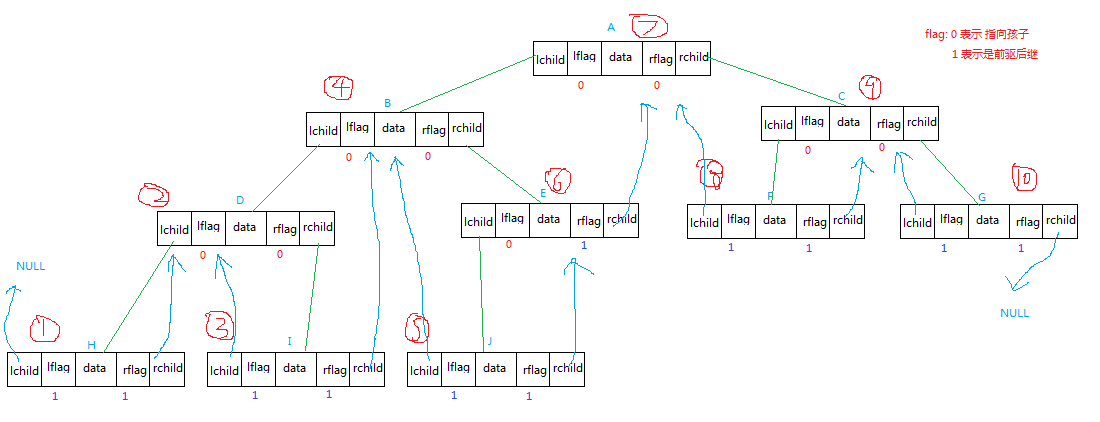
我们通过
(1)H的right-child来指向他的后继节点D,因为该节点没有前驱,索引左孩子指向NULL
(2)由于D没有空闲指针,所以不操作。
(3)该节点I的后驱是结点B,所以right-child指向B。其前驱是D,所以left-child指向D。
(4)没有空闲指针,不操作。
(5)left-child 指向B,right-child指向E
(6)只有右空闲指针:所以right-child指向A
(7)不操作
(8)F的前驱是A,后继是C
(9)不操作
(10)前驱是C,后继无,则指向NULL
线索化是在遍历过程中实现的:
现在将中序遍历和中序线索化代码做对比:
中序遍历:
void midVisitTree(pBitree T) { if (T == NULL) { return ; } midVisitTree(T->lch); printf(" %c ",T->data); midVisitTree(T->rch);
}
中序线索化:
void midThrTree(pBitree T) { if (T == NULL) { return ; } midThrTree(T->lch); if (T->lch == NULL) { T->lf = Thread; T->lch = pre; } if (pre != NULL && pre->rch == NULL) { pre->rf = Thread; pre->rch = T; } pre = T; midThrTree(T->rch); }
比较发现,
printf(" %c ",T->data);
变成了
if (T->lch == NULL) { T->lf = Thread; T->lch = pre; } if (pre != NULL && pre->rch == NULL) { pre->rf = Thread; pre->rch = T; } pre = T;
线索化过程:
遍历到中序排序的第一个节点时:
第一个if块:pre是全局指针,初始值为NULL。这有递归调用找到中序遍历第一个节点,并将其left-flag 设置为 线索(Thread),由于其前驱无,则赋值为pre(NULL)。
第二个if块:由于pre为NULL,故不执行。
其他情况时候:
第一个if块:pre记录的是上一个访问到的节点,所以该节点的前驱为pre。
第二个if块:将pre的后继指向当前节点,完成了后继的操作。
完成了线索化,现在要遍历整个树。
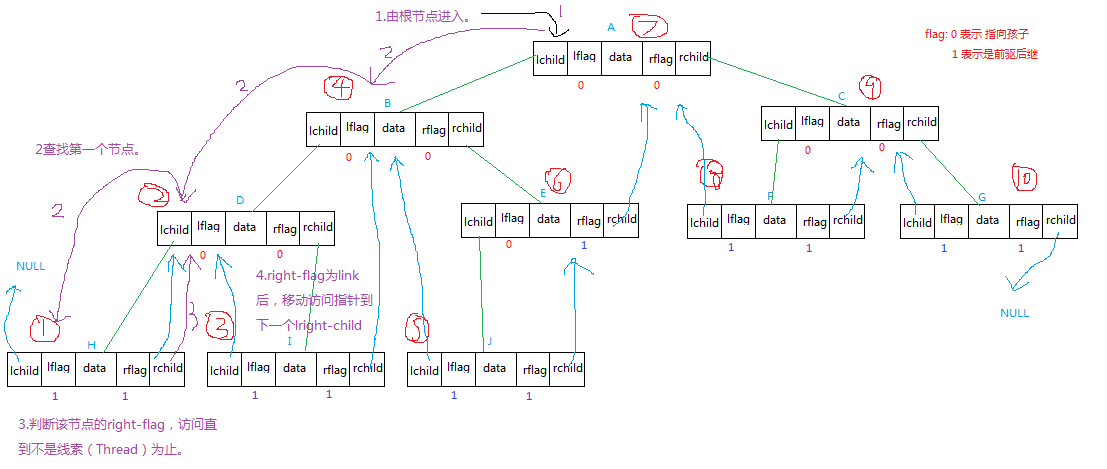
思想:
对任意节点
(1)判断是否有左边孩子,有则索引,直到左边孩子为NULL;
(2)判读右边是否为索引(Thread),索引至有右孩子的节点为止。
(3)索引有右孩子节点的右孩子。
(4)重复(1)(2)(3)。
由于中序遍历是从左、中、右顺序决定的。
代码:
void midVisitThrTree(pBitree T) { pBitree pos = T; while (pos != NULL) { while(pos->lf == Link) { pos = pos->lch; } printf(" %c ",pos->data); while(pos->rf == Thread && pos->rch != NULL) { pos = pos->rch; printf(" %c ",pos->data); } pos = pos->rch; } }
完整代码如下:
包括:节点的结构,前序建立树,中序遍历线索化树,线索化遍历。
// thr_bintree.cpp : 定义控制台应用程序的入口点。 // #include "stdafx.h" #include <stdlib.h> typedef char ElemType; typedef enum {Link,Thread} nodeType; typedef struct node{ ElemType data; struct node* lch; struct node* rch; nodeType lf; nodeType rf; }Bitree,*pBitree; pBitree pre = NULL; ElemType *g_str = "ABDH##I##EJ###CF##G##"; ElemType *g_strpos = NULL; pBitree g_head = NULL; void createTreeByPre(pBitree* T) { // printf("visis:%c\n",*g_strpos); if ( *g_strpos == '#') { *T = NULL; return ; } else { *T = (pBitree)malloc(sizeof(Bitree)); (*T)->data = *g_strpos; (*T)->lf = Link; (*T)->rf = Link; g_strpos++; // printf("left:%c\n",*g_strpos); createTreeByPre(&((*T)->lch)); g_strpos++; // printf("right:%c\n",*g_strpos); createTreeByPre(&((*T)->rch)); } } void midThrTree(pBitree T) { if (T == NULL) { return ; } midThrTree(T->lch); if (T->lch == NULL) { T->lf = Thread; T->lch = pre; } if (pre != NULL && pre->rch == NULL) { pre->rf = Thread; pre->rch = T; } pre = T; midThrTree(T->rch); } void midVisitThrTree(pBitree T) { pBitree pos = T; while (pos != NULL) { while(pos->lf == Link) { pos = pos->lch; } printf(" %c ",pos->data); while(pos->rf == Thread && pos->rch != NULL) { pos = pos->rch; printf(" %c ",pos->data); } pos = pos->rch; } } void preVisitTree(pBitree T) { if (T == NULL) { return ; } else { printf(" %c ",T->data); preVisitTree(T->lch); preVisitTree(T->rch); } } void midVisitTree(pBitree T) { if (T == NULL) { return ; } else { midVisitTree(T->lch); printf(" %c ",T->data); midVisitTree(T->rch); } } int _tmain(int argc, _TCHAR* argv[]) { pBitree treeHead; g_strpos = g_str; createTreeByPre(&treeHead); midVisitTree(treeHead); getchar(); midThrTree(treeHead); midVisitThrTree(treeHead); getchar(); return 0; }
结果:

第一排:中序遍历结果。
第二批:线索化后,中序线索化遍历结果。
补充:
还可以通过增加一个节点(总节点),来接受第一个节点的前驱,和最后一个节点的后继。这有就形成了一个双向链表。
具体可以自己实现。