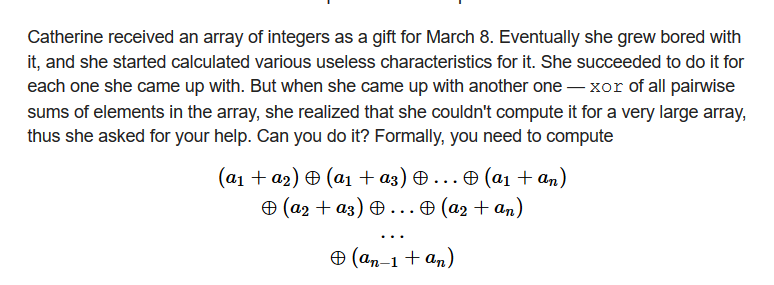这道题在做的时候一点思路都没有,感觉无从下手想过计算最后每一位是什么,从而计算结果但是还是感觉无从下手。
看了看题解,感觉豁然开朗
当我们要计算最后的结果中第k位是0还是1时,它与每个数的[k+1, )是没有关系的,所以当我们求每一位是,对所有的数取其[1 — k] 位;
得数组a;
若x + z >= (1<<k) && x + z <= (1<<(k+1)) - 1, 或 x + z >= (1<<(k+1)) + (1 << (k));
x,z均 < 1<< (k+1) 所以 x+z一定小于 1<<(k+2);
#include<bits/stdc++.h> using namespace std; #define ll long long #define inf 1000000000 int _pow[30] = {0}; int a[400005] = {0}, b[400005] = {0}; int n; int can(int k){ ll res = 0; for(int i = 1; i <= n; i++) b[i] = a[i]%(1<<(k+1)); sort(b+1, b + 1 + n); for(int i = 1; i <= n; i++){//求可以与x组队的个数 int x = b[i];
//若x与x可组队,则结果应减一。排数(i,i); if(x+x >= _pow[k] && x + x < _pow[k+1]-1) res--; if(x+x >= _pow[k] + _pow[k+1] ) res--; res += upper_bound(b+1, b+1+n, _pow[k+1]-1-x) - lower_bound(b+1, b+1+n, _pow[k]-x); res += upper_bound(b+1, b+1+n, inf) - lower_bound(b+1, b+1+n, _pow[k] + _pow[k+1] - x ); } return res/2%2; } int main() { for(int i = 0; i <= 29; i++) _pow[i] = (1<<i); scanf("%d", &n); for(int i = 1; i <= n; i++) scanf("%d", &a[i]); int sum = 0; for(int i = 0; i <= 25; i++) if(can(i)) sum += (1<<i); printf("%d ", sum); }
这个题为啥可以这样做?因为它选的·是两个元素相加后再分别异或。