POJ3696 欧拉定理

看了两天，poj还卡溢出。

题意

　　给你一个数L(2e9)，找到最小的连续8组成的数且是L的倍数。没有则输出0。

思路

　　首先8个连续的数可以表示为（10^x -1)*8/9。

　　（10^x -1)*8/9 = L*k（k为任意整数）

　　（10^x -1)*8 = L*k*9

　　令d = gcd（8，L）。

　　则两边同时除d

　　（10^x -1)*(8/d) = k*(L*9)/d

　　由a*b=c*d且a，c互质，能推出b|c可得

　　10^x -1|9*L/d

 　　ze可以

 

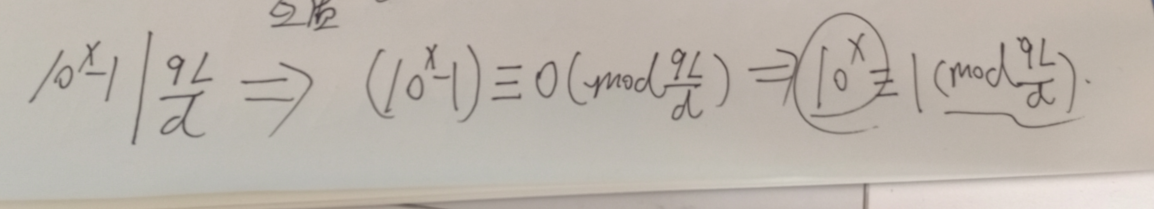
 　　然后答案即为9L/d 的欧拉函数的约数。如果10和9L/d不互质，则无解。

　　注意这题快速幂会溢出。

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;
typedef long long ll;
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
const int maxn = 2e5+10;
ll L;
ll phi(ll n)
{
    ll ans = n;
    for(int i = 2;i <= sqrt(n); ++i){
        if(n % i == 0){
            ans = ans/i * (i-1);
            while(n%i==0) n/=i;
        }

    }
    if(n > 1) ans = ans/n*(n-1);
    return ans;
}
ll powmod(ll a, ll b, ll mod)
{
    ll sum = 1;
    while (b) {
            if (b & 1) {
            sum = (sum * a) % mod;b--;
        }
        b /= 2;a = a * a % mod;
    }
    return sum;
}
int main()
{
    //freopen("input.txt", "r", stdin);
    int casee = 0;
    while(scanf("%lld",&L) != EOF){
        if(L == 0) break;
        ll d = gcd(L,8ll);
        ll p = 9*L/d;
        if(gcd(10,p) == 1){
            ll k = phi(p);
            bool flag = 0;
            for(int i = 1;i <= sqrt(k);++i){
                if(k%i==0 && powmod(10,i,p)==1){
                    printf("Case %d: %d
",++casee,i );
                    flag = 1;
                    break;
                }
            }
            if(flag == 1) continue;
            for(int i = sqrt(k);i >= 1;--i){
                if(k%i==0 && powmod(10,k/i,p)==1){
                    printf("Case %d: %d
",++casee,k/i );
                    break;
                }
            }
        }else printf("Case %d: 0
",++casee );
    }
}