一、问题定义
1.定义
黄金点游戏:N个玩家,每人写一个或两个0~100之间的有理数 (不包括0或100),提交给服务器,服务器在当前回合结束时算出所有数字的平均值,然后乘以0.618,得到G值。 提交的数字最靠近G(取绝对值)的玩家得到N分,离G最远的玩家得到-2分,其他玩家得0分。 只有一个玩家参与时不得分。
在我们的游戏中,每个玩家可以提交两个数字,一共十一组(包括邹欣老师),二十二个数字计算平均数然后乘0.618得到黄金数G。
2.难点
此游戏难点在于以下几处:
(1)参加游戏人数较多,每个人的策略完全不同且未知,因此很难有具体的理论推导能准确估计出一轮的黄金点。
(2)赢者通吃机制。获胜一次可以获得大量得分,而失败一次只会扣除2分。因此,是否需要战略性失败以搅乱黄金点分布平衡是一个需要考虑的问题,将它与一般只是为了获取分数的策略相结合可能可以获得好的结果。
(3)是采用最简单的策略还是和强化学习或者深度强化学习一起使用,要根据实际结果来评判,而不是直接能通过定性定量分析得到结果。
二、方法建模
我们在实验过程中采用了两种算法,分别是最简单的利用q-learning方法和Deep q-learning Network方法。下面分别介绍。
1.q-learning方法
QLearning是强化学习算法中value-based的算法,Q即为Q(s,a)就是在某一时刻的 s 状态下(s∈S),采取 动作a (a∈A)动作能够获得收益的期望,环境会根据agent的动作反馈相应的回报reward r,所以算法的主要思想就是将State与Action构建成一张Q-table来存储Q值,然后根据Q值来选取能够获得最大的收益的动作。
|
Q-Table |
a1 |
a2 |
|
s1 |
q(s1,a1) |
q(s1,a2) |
|
s2 |
q(s2,a1) |
q(s2,a2) |
|
s3 |
q(s3,a1) |
q(s3,a2) |
然后我们采用时间差分方法推导更新公式。时间差分方法结合了蒙特卡罗的采样方法和动态规划方法的bootstrapping(利用后继状态的值函数估计当前值函数)使得他可以适用于model-free的算法并且是单步更新,速度更快。值函数计算方式如下:
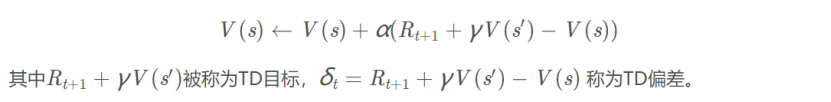
根据以上推导可以对Q值进行计算,所以有了Q值我们就可以进行学习,也就是Q-table的更新过程,其中α为学习率γ为奖励性衰变系数,采用时间差分法的方法进行更新。
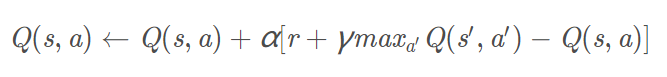
上式就是Q-learning更新的公式,根据下一个状态s’中选取最大的Q(s′,a′)值乘以衰变γ加上真实回报值即为Q现实,而根据过往Q表里面的Q(s,a)作为Q估计。
具体算法如下:

在这个方法中,我们采取的策略就是修改各项超参数与采取的action。将学习率,e-greedy等几个参数分别设置四个不同梯度的值,然后做了64组实验,找到了最佳的参数搭配。其次,在action中,本来提交的两个数字都是一样的,这无疑是不行的,相当于我们拿一个数字与别人两个数字竞争,因此我们将返回的两个数字分别用上一次黄金点,上一次黄金点*0.618,倒数第二次黄金点,倒数第二次黄金点*0.618,过去三次黄金点,过去三次黄金点*0.618,过去五次黄金点,过去五次黄金点*0.618,过去两个黄金点的几何平均、算术平均来相互搭配,得到八个不同的action。
同时我们也采用了提交不同数量99的action来进行随机扰乱,发现这使黄金点变化起伏更加明显,从而使得很多模型预测失准。
2.Deep Q Learning算法
与传统Q Learning算法相比,DQN不用Q表记录Q值,而是用神经网络来预测Q值,并通过不断更新神经网络从而学习到最优的行动路径。
他们将历史黄金点列表转换成深度神经网络的输入数据(状态s),用CNN(卷积神经网络)来预测动作a(a1,a2,a3 ....), 和对应的Q(s, a1), Q(s, a2),Q(s, a3)...然后算法通过更新神经网络(NN)中的参数(w, b ...),来更新NN,从而优化模型得到最优解。
DQN中有两个神经网络(NN)一个参数相对固定的网络,我们叫做target-net,用来获取Q-目标(Q-target)的数值, 另外一个叫做eval_net用来获取Q-评估(Q-eval)的数值。反向传播真正训练的网络是只有一个,就是eval_net。target_net 只做正向传播得到q_target (q_target = r +γ*max Q(s,a)). 其中 Q(s,a)是若干个经过target-net正向传播的结果。
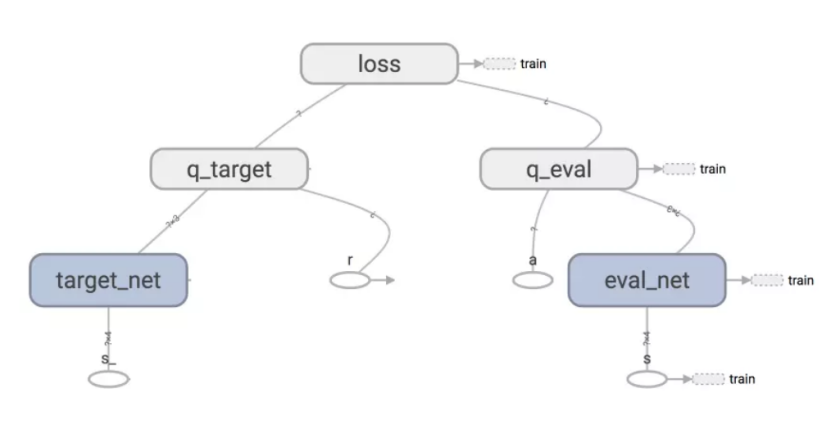
训练的数据是从记忆库中随机提取的,记忆库记录着每一个状态下的行动,奖励,和下一个状态的结果(s, a, r, s')。记忆库的大小有限,当记录满了数据之后,下一个数据会覆盖记忆库中的第一个数据,记忆库就是这样覆盖更新的。
q_target的网络target_net也会定期更新一下参数,由于target_net和eval_net的结构是一样的。更新q_target网络的参数就是直接将q_eval 的参数复制过来就行了。
随机抽取记忆库中的数据进行学习,打乱了经历之间的相关性,使得神经网络更新更有效率,Fixed Q-targets 使得target_net能够延迟更新参数从而也打乱了相关性。
具体算法如下:

在我们的实验实现中,我们将输入state到定义的网络Q中,得到n个输出,其中n为action的数目,每个输出代表了采用该action的得分。然后根据这个回合实际选择的action和执行它后得到的next state,就可以计算出该action对应的一个奖赏(惩罚),用这个奖赏(惩罚)就可以更新网络参数。同时,DQN具有一个记忆单元,每次从中采样出若干个样本来作为一个batch更新网络,而不是仅使用最近的这一次的数据。
三、结果分析
在自己开房间试验了q-learning和DQN网络的两个机器人后,我们发现DQN网络在一开始可能会得分高于q-learning方法,但到了后期就会被q-learning方法远远甩开。因此,我们提交时只采用了q-learning方法。
在第一天的1000回合比赛中,结果大大超出我们预期。本来以为我的bot2会输给其他采用DQN的bot,但是事实结果是我们排在了第二名,并且领先后面几名好几百分。在第二天的10000回合之中,我觉得我的机器人应该是会排在第二名,结果没想到过程跌宕起伏。一开始我们得分极低,排在很后面,但是到了中期,我们突然发力,远远甩开第三名,与第一名只差100多分。到了3000回合以后,我的bot2一直稳定在第一名,领先第二名400分左右。本以为可以开把黑准备躺赢,没想到到了8500回合时,第一天的第一名突然超过我的bot2。这还不算什么,到了9970回合时(一共10000回合),原本比我们低400多分的第三名居然超过了我们,最终剩余三十个回合我回天乏术,惜败40分。真的是太难了!不过过程是真的精彩!
在正式比赛前,我们认为评估模型好坏应该不仅是最终得分,而是中间过程的得分和排名情况,以及最后的相对得分差。例如我们bot2落后第二名40分,其实我们得了14000多分,那么这40分其实看来可能是由于偶然因素导致的。如果继续跑下去,很有可能第二名会被我们反超。
如果采用更多人或者更多数来比赛。我们的方法一定适用,因为我们最终采取的是最简单的修改action策略,他不容易受其他使用RNN,DQN等复杂神经网络的影响,具有更好的鲁棒性。
最后是对队友的评价。因为我的队友退课了,所以整个黄金点游戏的过程,从理解到写代码,测试,维护都是我一个人做的,最后还能拿到第三名,并且只比第一第二低了一点点,还是比较满意的!