ECDSA—模加减模块

　　如果a,b GF(P),则加法运算a+b=r (mod p),其中r满足0<r<p-1,即a+b除以p的余数，该操作成为模p加法。对于模减运算可以视为另类的模加运算，即a+(-b)=k (mod p)。本模块将模加和模减集中在同一模块中，由外部信号控制选择使用模减或者模减运算。

                                                                                                                              

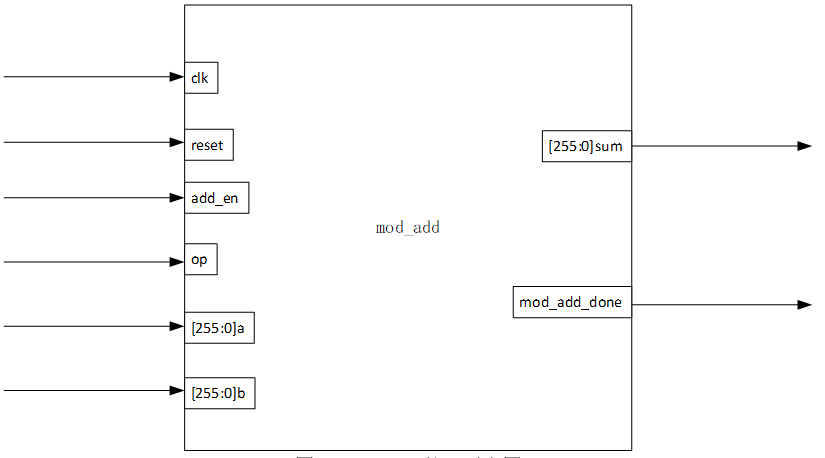
信号名	方向	位宽	端口定义
clk	Input	1	时钟
reset	Input	1	复位信号
add_en	Input	1	运算使能信号
op	Input	1	模加减选择信号
a	Input	256	整数a输入
b	Input	256	整数b输入
sum	Output	256	运算结果
mod_add_done	Output	1	模加减完成标识

　　代码如下：

    // op = 1, a-b mod p
    // op = 0, a+b mod p

module mod_add(
    input             clk,
    input             reset,
    input             en,
    input     [255:0] a,
    input     [255:0] b,
    input             op,
    output     reg [255:0] sum,
    output     reg mod_add_done
);
    parameter params_p=256'd15424654874903;
    //parameter params_p = 256'hFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F;

    reg [256:0] temp1;//temp2;                    //the [256] is the sign bit
    
    
    reg [1:0] cs,ns;
    parameter idle = 0;
    parameter s1 = 1;
    parameter s2 = 2;
    parameter s3 = 3;
    
    always@(posedge clk) begin
        if(reset)
            cs <= idle;
        else    
            cs <= ns;
    end

    always@(*) begin
        case(cs)
        idle:
            ns <= s1;
        s1:
            ns <= s2;
        s2:
            if(temp1[256])
                ns <= s2;
            else if(temp1 >= params_p)
                ns <= s2;
            else
                ns <= s3;
        s3:
            ns <= en ? idle : s3;
        endcase
    end

    always@(*) begin
        case(cs)
        idle: begin
            sum <= 0;
            mod_add_done <= 0;
        end
        s1:
            if(op) begin
                temp1 <= a - b;
                //temp2 = temp1 + params_p;
            end
            else begin
                temp1 <= a + b;
                //temp2 = temp1 - params_p;
            end
        s2:    
            if(op) begin
                if(temp1[256])    begin                //if temp1[256] is 1, 'a<b', 'a-b mod p' = 'params_p+(b-a)'
                    temp1 <= temp1 + params_p;
                end
                else if(temp1 >= params_p)
                    temp1 <= temp1 - params_p;
            end
            else begin
                if(temp1 >= params_p)                //if temp1[256] is 1, 'a<b', 'a-b mod p' = 'params_p-(b-a)'
                    temp1 <= temp1 - params_p;
                //else
                    //temp2 = temp1;
            end
        s3: begin
            sum <= temp1[255:0];
            mod_add_done <= 1;
        end
        endcase
    end
    
endmodule

选用的曲线参数如下：https://blog.csdn.net/cccchhhh6819/article/details/100660139

testbeach：

`timescale 1ns/1ns

module mod_add_tb();

    reg clk, reset,en;
    reg [255:0] a, b;
    wire [255:0] sum;
    reg op;
    wire    mod_add_done;

    mod_add add0(
        .clk(clk),
        .reset(reset),
        .en(en),
        .a(a),
        .b(b),
        .sum(sum),
        .op(op),
        .mod_add_done(mod_add_done)
    );
    
    always #5 clk = ~clk;

    initial begin
        clk = 0;

        reset = 1'b1;
        en = 0;
        
        #20
        reset = 1'b0;
        op = 1;//P=29
        a = 256'd15424654874903;
        b =256'd15424654874906;
　　　　 #10000 $stop; 

end endmodule

本次仿真计算的是a-b(mod p)  也即15424654874903 - 15424654874906（mod 15424654874903 ）的结果，相当于是-3 mod 15424654874903 。

仿真结果如下：为15424654874900。负数模运算规则 比如-2 mod 5 = -2+5=3 。-6 mod 5 = -6+5+5=4。所有结论正常。

当然我们更关注的是整个算法消耗的资源，这里博主还没学到综合那里去，后续会跟进这部分。当然该算法应该会占用较大的资源，毕竟用到了两个位宽的寄存器直接相加，会延迟寄存器之间的关键路径，导致最后时钟频率跑不上去。