Description
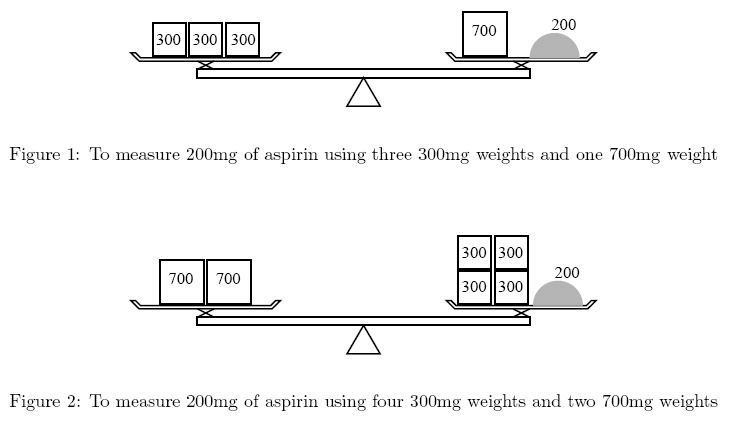
Ms. Iyo Kiffa-Australis has a balance and only two kinds of weights to measure a dose of medicine. For example, to measure 200mg of aspirin using 300mg weights and 700mg weights, she can put one 700mg weight on the side of the medicine and three 300mg weights on the opposite side (Figure 1). Although she could put four 300mg weights on the medicine side and two 700mg weights on the other (Figure 2), she would not choose this solution because it is less convenient to use more weights.
You are asked to help her by calculating how many weights are required.
You are asked to help her by calculating how many weights are required.

Input
The input is a sequence of datasets. A dataset is a line containing three positive integers a, b, and d separated by a space. The following relations hold: a != b, a <= 10000, b <= 10000, and d <= 50000. You may assume that it is possible to measure d mg using a combination of a mg and b mg weights. In other words, you need not consider "no solution" cases.
The end of the input is indicated by a line containing three zeros separated by a space. It is not a dataset.
The end of the input is indicated by a line containing three zeros separated by a space. It is not a dataset.
Output
The output should be composed of lines, each corresponding to an input dataset (a, b, d). An output line should contain two nonnegative integers x and y separated by a space. They should satisfy the following three conditions.
No extra characters (e.g. extra spaces) should appear in the output.
- You can measure dmg using x many amg weights and y many bmg weights.
- The total number of weights (x + y) is the smallest among those pairs of nonnegative integers satisfying the previous condition.
- The total mass of weights (ax + by) is the smallest among those pairs of nonnegative integers satisfying the previous two conditions.
No extra characters (e.g. extra spaces) should appear in the output.
Sample Input
700 300 200 500 200 300 500 200 500 275 110 330 275 110 385 648 375 4002 3 1 10000 0 0 0
Sample Output
1 3 1 1 1 0 0 3 1 1 49 74 3333 1
#include<cstdio> #include<set> #include<map> #include<cstring> #include<algorithm> #include<queue> #include<iostream> #include<string> #include<cmath> #include<vector> using namespace std; typedef long long LL; /* a*x = b*y + d a*x + b*y = d |x|+|y| 的最小值 |x|+|y|==|x0+b/d*t|+|y0-a/d*t|,我们规定 a>b(如果 a<b,我们便交换 a b),从这个式子中, 我们可以轻易的发现:|x0+b/d*t|是单调递增的,|y0-a/d*t|是单调递减的,而由于我们规定了 a>b, 那么减的斜率边要大于增的斜率,于是整个函数减少的要比增加的快,但是由于绝对值的符号的作用, 最终函数还是递增的。 也就是说,函数是凹的,先减小,再增大。那么什么时候最小呢?很显然是 y0-a/d*t==0 的时候, 于是我们的最小值|x|+|y|也一定是在 t=y0*d/a附近了,只要在附近枚举几个值就能找到最优解了。 */ typedef long long LL; #define INF 0x3f3f3f3f LL ex_gcd(LL a,LL b,LL &x,LL &y) { if(b==0) { x = 1; y = 0; return a; } LL ans = ex_gcd(b,a%b,x,y); LL tmp = x; x = y; y = tmp - a/b*x; return ans; } void cal(LL a,LL b,LL c)//求ax+by==c 的一组|x|+|y| 最小的解 { bool f = false; if(a<b) { f = true; swap(a,b); } LL x=0,y=0; LL gcd = ex_gcd(a,b,x,y); x *= c/gcd; y *= c/gcd; LL t = y*gcd/a,ans=INF; LL kx,ky; for(LL i=t-1;i<=t+1;i++) { LL t1 = x + (b/gcd)*i; LL t2 = y - (a/gcd)*i; if( abs((long)t1)+abs((long)t2)<ans) { ans = abs((long)t1)+abs((long)t2); kx = (t1>0)?t1:-t1; ky = (t2>0)?t2:-t2; } } if(!f) printf("%lld %lld ",kx,ky); else printf("%lld %lld ",ky,kx); } int main() { LL a,b,c; while(scanf("%lld%lld%lld",&a,&b,&c),a+b+c) { cal(a,b,c); } }