基准时间限制:1 秒 空间限制:131072 KB 分值: 0 难度:基础题
斐波那契数列的定义如下:
F(0) = 0
F(1) = 1
F(n) = F(n - 1) + F(n - 2) (n >= 2)
(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...)
给出n,求F(n),由于结果很大,输出F(n) % 1000000009的结果即可。
Input
输入1个数n(1 <= n <= 10^18)。
Output
输出F(n) % 1000000009的结果。
运用矩阵乘法去做,有矩阵,可以矩阵快速幂求出转移矩阵即可得到结果。
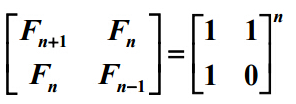
#include<iostream> #include<algorithm> #include<cstdio> using namespace std; typedef long long LL; int n = 2; struct mat { LL a[2][2]; }; mat mul(mat m1,mat m2) { mat ans; for(int i=0;i<n;i++) for(int j=0;j<n;j++) { LL temp = 0; for(int k=0;k<n;k++) { temp+=m1.a[i][k]*m2.a[k][j]; } ans.a[i][j] = temp % 1000000009; } return ans; } mat pow(mat m,LL b) { if(b<=1) return m; mat temp = pow(m,b/2); if(b&1) return mul(mul(temp,temp),m); else return mul(temp,temp); } int main() { LL num; mat beg; beg.a[0][0]=beg.a[0][1]=beg.a[1][0]=1;beg.a[1][1]=0; cin>>num; cout<<pow(beg,num-1).a[0][0]<<endl; return 0; }
在2*N的一个长方形方格中,用一个1*2的骨牌排满方格。

问有多少种不同的排列方法。
例如:2 * 3的方格,共有3种不同的排法。(由于方案的数量巨大,只输出 Mod 10^9 + 7 的结果)

Input
输入N(N <= 1000)
Output
输出数量 Mod 10^9 + 7
Input示例
3
Output示例
3
显然,N=1时一种方法,N=2时有两种方法。
当N>2,可分为两种情况,1是竖着放,那么方法数目为前n-1个的结果,f(n-1)
2是两个横着放,这样占用了两个格子,方法数目是前n-2个结果 f(n-2)
f(n)=f(n-1)+f(n-2),f(1)=1,f(2)=2;
由上面程序略作修改
#include<iostream> #include<algorithm> #include<cstdio> using namespace std; typedef long long LL; int n = 2; #define M 1000000007 struct mat { LL a[2][2]; }; mat mul(mat m1,mat m2) { mat ans; for(int i=0;i<n;i++) for(int j=0;j<n;j++) { LL temp = 0; for(int k=0;k<n;k++) { temp+=m1.a[i][k]*m2.a[k][j]; } ans.a[i][j] = temp%M; } return ans; } mat pow(mat m,LL b) { if(b<=1) return m; mat temp = pow(m,b/2); if(b&1) return mul(mul(temp,temp),m); else return mul(temp,temp); } int main() { LL num; mat beg; beg.a[0][0]=beg.a[0][1]=beg.a[1][0]=1;beg.a[1][1]=0; cin>>num; mat tmp; tmp.a[0][0]=2,tmp.a[0][1]=tmp.a[1][0]=1,tmp.a[1][1]=0; mat r = pow(beg,num-1); mat as=mul(tmp,r); cout<<as.a[0][1]<<endl; return 0; }
基准时间限制:1 秒 空间限制:131072 KB 分值: 10 难度:2级算法题
有一个序列是这样定义的:f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.
给出A,B和N,求f(n)的值。
Input
输入3个数:A,B,N。数字之间用空格分割。(-10000 <= A, B <= 10000, 1 <= N <= 10^9)
Output
输出f(n)的值。
同样思路用矩阵做,注意避免负数的出现 (ans+7)%7.只需把递归式中系数修改。
#include<iostream> #include<algorithm> #include<cstdio> using namespace std; typedef long long LL; int n = 2; #define M 1000000007 struct mat { LL a[2][2]; }; mat mul(mat m1,mat m2) { mat ans; for(int i=0;i<n;i++) for(int j=0;j<n;j++) { LL temp = 0; for(int k=0;k<n;k++) { temp+=m1.a[i][k]*m2.a[k][j] ; } ans.a[i][j] = (temp+7)%7; } return ans; } mat pow(mat m,LL b) { if(b<=1) return m; mat temp = pow(m,b/2); if(b&1) return mul(mul(temp,temp),m); else return mul(temp,temp); } int main() { LL num,t1,t2; cin>>t1>>t2>>num; mat beg; beg.a[0][0]=t1,beg.a[0][1]=t2,beg.a[1][0]=1;beg.a[1][1]=0; mat r = pow(beg,num-2); cout<<(r.a[0][0]+r.a[0][1]+7)%7<<endl; return 0; }