算法—8.有序数组中的二分查找

1.具体算法

/**
 * 算法3.2 二分查找（基于有序数组）
 * Created by huazhou on 2015/11/29.
 */
public class BinarySearchST<Key extends Comparable<key>, Value> {
    private Key[] keys;
    private Value[] vals;
    private int N;

    public BinarySearchST(int capacity){
        keys = (Key[])new Comparable[capacity];
        vals = (Value[])new Object[capacity];
    }

    public int size(){
        return N;
    }

    public boolean isEmpty() {
        return size() == 0;
    }

    public Value get(Key key){
        if(isEmpty()){
            return null;
        }
        int i = rank(key);
        if(i < N && keys[i].compareTo(key) == 0){
            return vals[i];
        }
        else{
            return null;
        }
    }

    public int rank(Key key){
        int lo = 0, hi = N-1;
        while (lo <= hi) {
            int mid = lo + (hi - lo) / 2;
            int cmp = key.compareTo(keys[mid]);
            if      (cmp < 0) hi = mid - 1;
            else if (cmp > 0) lo = mid + 1;
            else return mid;
        }
        return lo;
    }

    //查找键，找到则更新值，否则创建新的元素
    public void put(Key key, Value val){
        int i = rank(key);
        if(i < N && keys[i].compareTo(key) == 0){
            vals[i] = val;
            return;
        }
        for (int j = N; j > i; j--){
            keys[j] = keys[j-1];
            vals[j] = vals[j-1];
        }
        keys[i] = key;
        vals[i] = val;
        N++;
    }

    public void delete(Key key){
        if (isEmpty()) return;

        // compute rank
        int i = rank(key);

        // key not in table
        if (i == N || keys[i].compareTo(key) != 0) {
            return;
        }

        for (int j = i; j < N-1; j++)  {
            keys[j] = keys[j+1];
            vals[j] = vals[j+1];
        }

        N--;
        keys[N] = null;  // to avoid loitering
        vals[N] = null;

        // resize if 1/4 full
        if (N > 0 && N == keys.length/4) resize(keys.length/2);
    }
}

这段符号表的实现用两个数组来保存键和值。和基于数组的栈一样，put()方法会在插入新元素前将所有较大的键向后移动一格。

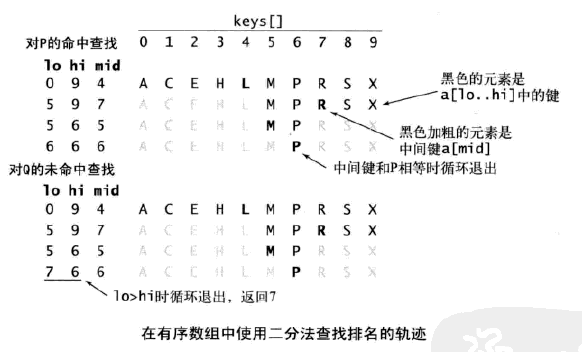
rank()方法实现了正文所述的经典算法来计算小于给定键的键的数量。它首先将key和中间键比较，如果相等则返回其索引；如果小于中间键则在左半部分查找；大于则在右半部分查找。

public Key min(){
        return keys[0];
    }

    public Key max(){
        return keys[N-1];
    }

    public Key select(int k){
        return keys[k];
    }

    public Key ceiling(Key key){
        int i = rank(key);
        return keys[i];
    }

    public Key floor(Key key){
        int i = rank(key);
        if (i < N && key.compareTo(keys[i]) == 0) return keys[i];
        if (i == 0) return null;
        else return keys[i-1];
    }

    public boolean contains(Key key) {
        return get(key) != null;
    }

    public Iterable<Key> keys(Key lo, Key hi){
        Queue<Key> q = new Queue<Key>();
        for (int i = rank(lo); i < rank(hi); i++){
            q.enqueue(keys[i]);
        }
        if(contains(hi)){
            q.enqueue(keys[rank(hi)]);
        }
        return q;
    }

2.算法分析

rank()的递归实现还能够让我们立即得到一个结论：二分查找很快，因为递归关系可以说明算法所需比较次数的上界。

命题：在N个键的有序数组中进行二分查找最多需要（lgN+1）次比较（无论是否成功）。

证明：这里的分析和对归并排序的分析类似（但相对简单）。令C(N)为在大小为N的符号表中查找一个键所需进行的比较次数。显然我们有C(0)=0，C(1)=1，且对于N>0我们可以写出一个和递归方法直接对应的归纳关系式：

C(N)<=C(_└N/2_┘)+1

无论查找会在中间元素的左侧还是右侧继续，子数组的大小都不会超过_└N/2_┘，我们需要一次比较来检查中间元素和被查找的键是否相等，并决定继续查找左侧还是右侧的子数组。当N为2的幂减1时（N=2ⁿ-1），这种递推很容易。首先，因为_└N/2_┘=2^n-1-1，所以我们有：

C(2ⁿ-1)<=C(2^n-1-1)+1

用这个公式代换不等式右边的第一项可得：

C(2ⁿ-1)<=C(2^n-2-1)+1+1

将上面这一步重复n-2次可得：

C(2ⁿ-1)<=C(2⁰)+n

最后的结果即：

C(N)=C(2ⁿ)<=n+1<lgN+1

对于一般的N，确切的结论更加复杂，但不难通过以上论证推广得到。二分查找所需时间必然在对数范围之内。

尽管能够保证查找所需的时间是对数级别的，BinarySearchST仍然无法支持我们用类似FrequencyCounter的程序来处理大型问题，因为put()方法还是太慢了。二分查找减少了比较的次数但无法减少运行所需时间，因为它无法改变以下事实：

在键是随机排列的情况下，构造一个基于有序数组的符号表所需要访问数组的次数是数组长度的平方级别（在实际情况下键的排列虽然不是随机的，但仍然很好地符合这个模型）。

命题：向大小为N的有序数组中插入一个新的元素在最坏情况下需要访问~2N次数组，因此向一个空符号表中插入N个元素在最坏情况下需要访问~N²次数组。

证明：同上命题。

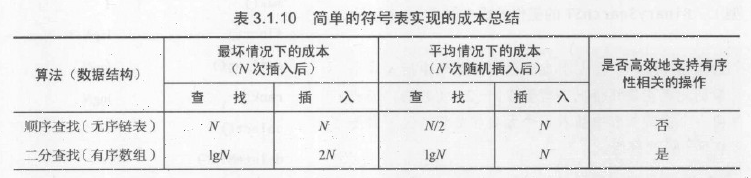
3.总结

一般情况下二分查找都比顺序查找快得多，它也是众多实际应用程序的最佳选择。当然，二分查找也不适合很多应用。例如，它无法处理Leipzig Corpora数据库，因为查找和插入操作是混合进行的，而且符号表也太大了。如我们所强调的那样，现代应用需要同时能够支持高效的查找和插入两种操作的符号表实现。也就是说，我们需要在构造庞大的符号表的同时能够任意插入（也许还有删除）键值对，同时也要能够完成查找操作。

【源码下载】