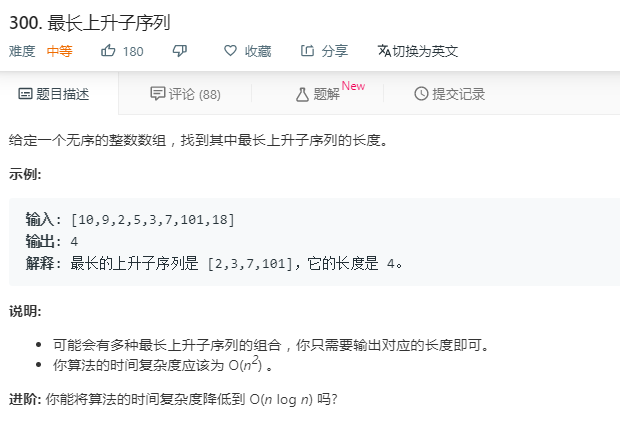
动态规划new version:
/** 维护一个数组DP[i]从0开始更新,为0->i且以i结尾的最长子序列的长度: for i: 0-->n for j: 0-->i if(nums[j]<nums[i]) DP[i]=max(DP[j]+1,DP[i]); 记录DP中最大值 初始化DP[i]:=1 **/ class Solution { public: int lengthOfLIS(vector<int>& nums) { int len=nums.size(); if(len==0) return 0; vector<int> DP(len,1); int res=0; for(int i=0;i<len;i++){ for(int j=0;j<i;j++){ if(nums[j]<nums[i])DP[i]=max(DP[j]+1,DP[i]); } res=max(res,DP[i]); } return res; } };
动态规划:O(n^2) 80ms
/*** 暴力求解:每个位置出现或者不出现,O(2^n) 动态规划:DP[i]代表从0到i且包括i的最长上升子序列的长度 DP[0]初值为1,其他DP[i]也可以赋值为1,视作为一个下降序列,然后从第2个元素递推 for i:0-->n-1 for j:0-->i-1 if(nums[j]<nums[i]) DP[i]=max(DP[i],DP[j]+1) ***/ class Solution { public: int lengthOfLIS(vector<int>& nums) { int len=nums.size(); if(len==0) return 0; int res=1; vector<int> dp(len,1); for(int i=1;i<len;i++){ for(int j=0;j<i;j++){ if(nums[j]<nums[i]){ dp[i]=max(dp[i],dp[j]+1); res=max(res,dp[i]); } } } return res; } };
二分查找:O(nlog(n))8ms
/*** 暴力求解:每个位置出现或者不出现,O(2^n) 动态规划:DP[i]代表从0到i且包括i的最长上升子序列的长度 DP[0]初值为1,其他DP[i]也可以赋值为1,视作为一个下降序列,然后从第2个元素递推 for i:0-->n-1 for j:0-->i-1 if(nums[j]<nums[i]) DP[i]=max(DP[i],DP[j]+1) 二分查找: a维护一个数组LIS b遍历: for i:0-->n-1 在LIS中查找大于等于nums[i]的第1个数LIS[j],LIS[j]=nums[i]; 若LIS中不存在,则LIS.push_back(nums[i]) c返回LIS.size()为答案; 注意:LIS不一定为序列的最长上升子序列,但是他的长度与子序列相等 ***/ class Solution { public: int lengthOfLIS(vector<int>& nums) { int len=nums.size(); if(len==0) return 0; vector<int> LIS; for(int n:nums){ vector<int>::iterator it=lower_bound(LIS.begin(),LIS.end(),n); if(it==LIS.end()) LIS.push_back(n); else *it=n; } return LIS.size(); } };
一个例子为:因为LIS是一个递增序列,因此可以用二分查找来得到结果
