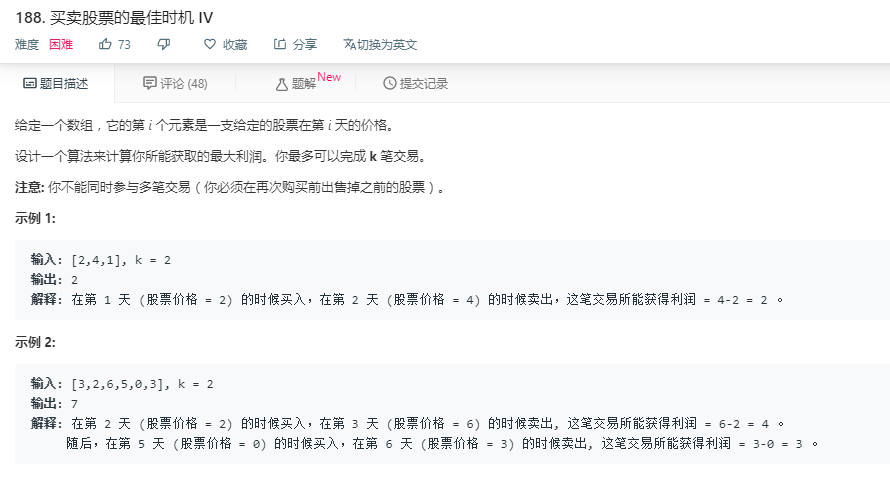
参见

本题采用了第一列初始化后,从左侧向右开始递推的方式,但从上往下递推应该也成立,以后尝试一下
想写一个普适性的适用于n天交易k次持有j股的状态方程但是有问题;对于交易次数过多的情况数组会超出界限:
测试数据:100
[106,373,495,46,359,919,906,440,783,583,784,73,238,701,972,308,165,774,990,675,737,990,713,157,211,880,961,132,980,136,285,239,628,221,948,939,28,541,414,180,171,640,297,873,59,814,832,611,868,633,101,67,396,264,445,548,257,656,624,71,607,67,836,14,373,205,434,203,661,793,45,623,140,67,177,885,155,764,363,269,599,32,228,111,102,565,918,592,604,244,982,533,781,604,115,429,33,894,778,885,145,888,577,275,644,824,277,302,182,94,479,563,52,771,544,794,964,827,744,366,548,761,477,434,999,86,1000,5,99,311,346,609,778,937,372,793,754,191,592,860,748,297,610,386,146,220,7,113,657,438,482,700,158,884,877,964,777,139,809,489,383,92,581,970,899,947,864,443,490,825,674,906,402,270,416,611,949,476,775,899,837,796,227,232,226,11,266,889,215,6,182,430,5,706,994,128,359,841,439,263,491,689,638,485,763,695,135,800,763,54,569,387,112,316,193,675,546,531,954,571,208,282,557,892,469,875,765,592,374,276,892,843,625,180,249,292,477,882,837,112,46,667,187,93,418,790,903,12,978,510,647,446,597,958,678,897,420]
时间复杂度O(n*k)空间复杂度O(n*k*2) k过大时空间超出,而且貌似这个代码是有问题的,因此先留待修改;
class Solution { public: int maxProfit(int K, vector<int>& prices) { //使用MP[i][k][j]作为状态数组,i代表第i天,k代表第k次交易,j值为0(未持有股票)和1(持有股票) int l=prices.size(); if(l<=1) return 0; int res=0; int MP[l][K+1][2]; //状态数组初始化 for(int i=0;i<l;i++){ MP[i][0][1]=0;//0次交易却持有股票 MP[i][0][0]=0; MP[i][1][0]=0;//不持有股票却有1次交易 MP[i][1][1]=-prices[i]; } for(int k=2;k<=K;k++){ MP[0][k][0]=0;//第一天有k笔交易不持有股票 MP[0][k][1]=0;//第一天有k笔交易持有股票 } //状态转移 for(int i=1;i<l;i++){ cout<<"i="<<i<<": "; for(int k=1;k<=K;k++){ MP[i][k][0]=max(MP[i-1][k][0],MP[i-1][k][1]+prices[i]); MP[i][k][1]=max(MP[i-1][k][1],MP[i-1][k-1][0]-prices[i]); cout<<"("<<MP[i][k][0]<<","<<MP[i][k][1]<<"),"; if(MP[i][k][0]>res) res=MP[i][k][0]; } cout<<endl; } return res; } };
那么针对leetcode188怎么优化空间复杂度呢,可以尝试去掉k这个维度来建立dp数组,为了明确意义,j维度也可以去掉,转而建立两个n维数组sell,buy来进行尝试
基于123的2次交易采用k维数组储存状态O(n*k)时间,O(k)空间,结果超时,k量级(10^10)超时,超空间,代码如下:
class Solution { public: int maxProfit(int k, vector<int>& prices) { int len=prices.size(); if(len<=1||k<=0) return 0; int res=0; vector<int> buy(k,INT_MIN); vector<int> sell(k,0); for(int price:prices){ for(int i=0;i<k;i++){ if(i==0) buy[0]=max(buy[0],-price); else buy[i]=max(buy[i],sell[i-1]-price); sell[i]=max(sell[i],buy[i]+price); } } return sell[k-1]; } };
基于leetcode122和123的结果:由于188交易次数过多时会极大的提升空间复杂度,因此考虑以下情况,当交易次数k>len/2时题目退化为122所以整体时间复杂度上限为1/2*n^2,消除了最坏情况下交易次数过多的case,beat95%,C++代码如下:
//从第0天之前开始初始化为-∞的buy和为0的sell
class Solution { public: int maxProfit(int k, vector<int>& prices) { int len=prices.size(); if(len<=1||k<=0) return 0; if(k>=len/2) return maxProfit122(prices); int res=0; vector<int> buy(k,INT_MIN); vector<int> sell(k,0); for(int price:prices){ buy[0]=max(buy[0],-price); sell[0]=max(sell[0],buy[0]+price); for(int i=1;i<k;i++){ buy[i]=max(buy[i],sell[i-1]-price); sell[i]=max(sell[i],buy[i]+price); } } return sell[k-1]; } int maxProfit122(vector<int>& prices){ int len=prices.size(); int res=0; for(int i=1;i<len;i++){ if(prices[i]>prices[i-1]) res+=prices[i]-prices[i-1]; } return res; } };
或者直接根据第一天的价格初始化buy和sell,避免价格过高或过低的异常
class Solution { public: int maxProfit(int k, vector<int>& prices) { int len=prices.size(); if(len<=1||k<=0) return 0; if(k>=len/2) return maxProfit122(prices); int res=0; vector<int> buy(k,-prices[0]); vector<int> sell(k,0); //sell和buy的下标代表第k次交易取值为0,1,2,………,k-1 for(int i=1;i<len;i++){ int price=prices[i]; buy[0]=max(buy[0],-price);//第i天第0次购买的股票是前i天(包括第i天)中价格最低的股票 sell[0]=max(sell[0],buy[0]+price);//前i天买入并卖出一次(第0次)获得的最大收益 for(int j=1;j<k;j++){ buy[j]=max(buy[j],sell[j-1]-price);//第i天第j次买入是i-1天以前买入j次和i天前卖出j-1次并第j天买入的比较 sell[j]=max(sell[j],buy[j]+price);//前i-1天买卖j次,和前i天买入第i天卖出的比较 } } return sell[k-1]; } int maxProfit122(vector<int>& prices){ int len=prices.size(); int res=0; for(int i=1;i<len;i++){ if(prices[i]>prices[i-1]) res+=prices[i]-prices[i-1]; } return res; } };