迁移学习
背景
- 传统的机器学习需要对每个领域都标定大量训练数据,一些新出现的领域中的大量训练数据非常难得到(数据缺失)。把已训练好的模型参数迁移到新的模型来帮助新模型训练,可以加速网络的学习和优化。
- 最终学习的效果靠的更多的还是模型的结构(表示能力)以及新数据集的丰富程度。
迁移学习(Transfer learning)——利用数据和领域之间存在的相似性关系,把之前学习到的知识,应用于新的未知领域。迁移学习的核心问题是,找到两个领域的相似性。

基本定义
- 域 可以理解为某个时刻的某个特定领域,比如书本评论和电视剧评论可以看作是两个不同的domain。包含两部分:feature space(特征空间)与probability(分布概率)
- 源与目标feature space相同:同构学习——常使用域适配Domain Adaptation方法
- 源与目标feature space不同:异构学习
- 任务 就是要做的事情,比如情感分析和实体识别就是两个不同的task。包含label space(标记空间)与objective predictive function(目标预测函数)
- 源:训练模型的域/任务,通常数据量很大;
- 目标:用前者的模型对自己的数据进行预测/分类/聚类等机器学习任务的域/任务,通常数据量小
关键点
- What to transfer:用哪些知识在不同的领域或者任务中进行迁移学习
- 如何进行迁移:如何设计出合适的算法来提取和迁移共有知识。
- 基于实例:从源域中挑选对目标领域的训练有用的实例,给予更大的权重(相当于扩充了与目标域相似样本的比例),使得两者的分布尽可能相同。instance reweighting(样本重新调整权重)和importance sampling(重要性采样)是常用的两项技术,参考了TrAdaBoost的思想。
- 基于特征:找出源领域与目标领域之间共同的特征表示,将源领域和目标领域的数据从原始特征空间映射到新的特征空间中,在该空间中,源领域数据与的目标领域的数据分布相同。
- 基于参数共享:找到源数据和目标数据的空间模型之间的共同参数或者先验分布
- 什么情况下适合迁移,实现避免负迁移,利用正迁移
深度神经网络的可迁移性
《How transferable are features in deep neural networks?》 NIPS 2014
说明了迁移学习的可行性,并提供了迁移方式的导向
实验方法
- 在ImageNet的1000类上,作者把1000类分成两份(A和B),基于Caffe对A和B两类分别训练一个 AlexNet 网络
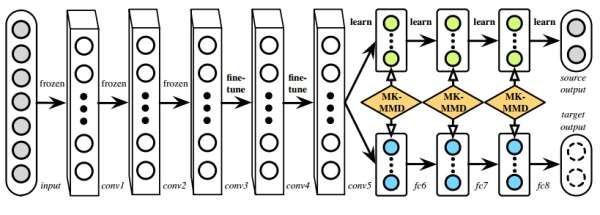
- 迁移A网络的某n层到B(AnB):将A网络的前n层拿来并将它frozen,剩下的8-n层随机初始化,然后对B进行分类。
- 固定B网络的某n层(BnB):把训练好的B网络的前n层拿来并将它frozen,剩下的8-n层随机初始化,然后对B进行分类。
实验结论
-
图像分类的网络前面几层都学习到的是通用的特征(general feature),随着网络的加深,后面的网络更偏重于学习特定的特征(specific feature)。随着可迁移层数的增加,使用了表示特定特征的网络层,模型性能一般会下降。
-
Fine-tune(微调)对模型结果有着很好的促进作用,可以比较好地克服数据之间的差异性
三种迁移学习方式
- Transfer Learning:冻结预训练模型的全部卷积层,只训练自己定制的全连接层。
- Fine-tune:冻结预训练模型的部分卷积层(通常是靠近输入的多数卷积层),训练剩下的卷积层(通常是靠近输出的部分卷积层)和全连接层。
- 目标域数据量少,但源域与目标域数据相似度非常高:只是修改最后几层或最终的softmax图层的输出类别。
- 目标域数据量数据量少,且数据相似度低:冻结预训练模型的初始层(比如k层),并再次训练剩余的(n-k)层。
- Extract Feature Vector:先计算出预训练模型的卷积层对所有训练和测试数据的特征向量,然后抛开预训练模型,只训练自己定制的简配版全连接网络。
深度迁移示例
PRICAI 2014的 DaNN(Domain Adaptive Neural Network)
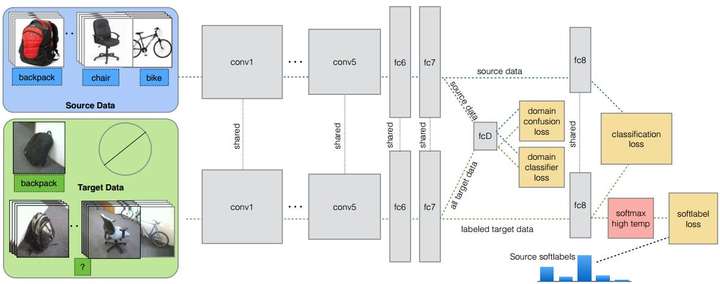
arXiv 2014的DDC(Deep Domain Confusion)
ICML 2015上的深度适配网络(Deep Adaptation Network, DAN) 三个例子展示了如何进行迁移学习
CVPR 2018 的 Maximum Classifier Discrepancy for Unsupervised Domain Adaptation
对于一个深度网络,随着网络层数的加深,网络越来越依赖于特定任务;不同任务的网络中,浅层的特征基本是通用的。
DaNN
- DaNN的结构异常简单,它仅由两层神经元组成:特征层和分类器层。在特征层后加入了一项MMD适配层(adaptation layer),用来计算源域和目标域的距离,并将其加入网络的损失中进行训练。
- MMD:把source和target用一个相同的映射映射在一个再生核希尔伯特空间(RKHS)中,然后求映射后两部分数据的均值差异。
- 整个网络的优化目标也相应地由两部分构成:在有label的源域数据上的分类误差(
),以及对两个领域数据的判别误差(
)。
- 问题:网络太浅,表征能力有限
DDC
- DDC针对预训练的AlexNet(8层)网络,在第7层(也就是feature层,softmax的上一层)加入了MMD距离来减小source和target之间的差异。
- 问题
- 只适配了一层网络,但可迁移的网络层不止一层;
- 用了单一核的MMD,单一固定的核可能不是最优的核。
DAN
- DAN用了多层适配和多核MMD(MK-MMD),效果比DDC更好。
- 它的优化目标由两部分组成:损失函数和分布距离。损失函数,用来度量预测值和真实值的差异;分布距离,用来表示不同域之间的差距。
- 多核MMD(Multi-kernel MMD,MK-MMD)
- 无法确定使用哪一种核方法更好,故而提出用多个核去构造总的核,利用m个不同的核方法(函数)加权得到,其表征能力较单核更强。
- 计算时,可以利用MK-MMD的无偏估计,降低计算的时间复杂度。
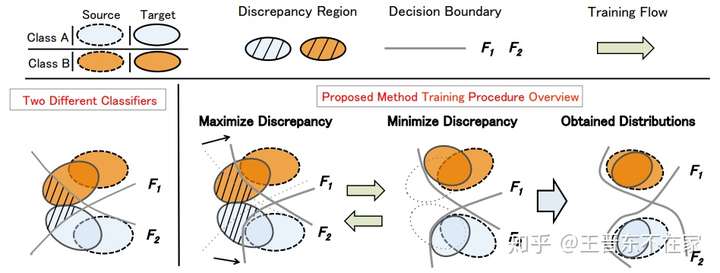
MCD_DA
领域自适应方法在适配过程中,并没有考虑任务特异性的决策边界,忽略了其实每个domain都有各自的特点。
引入了两个独立的分类器 和
,用二者的分歧(结果不一致)表示样本的置信度不高,需要重新训练。
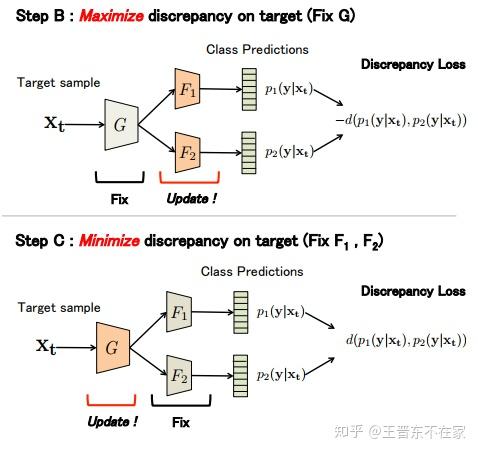
首先根据源域数据训练出两个不同的分类器 和
。之后B阶段,固定特征提取器G,更新两个分类器,使之差异最大化,C阶段固定分类器,优化特征提取器G,使两个分类器的效果尽可能一样。
域自适应
为使得针对源域的训练网络可以用于目标域,需要将源域与目标域的特征对齐等适配工作
GFK
源域数据(source)和目标域数据(target)类别一样,但是特征服从不同的分布。此时需要通过一个特征映射,把source和target变换到一个公共空间上,在这个空间里,它们的距离是最小的(相似度最高)。
把source和target分别看成高维空间(Grassmann流形)中的两个点,对两者最短连线上每一点积分(进行大量的变换),将source变换到target。
- 变换
- 针对给定的两个数据集
,对它们进行PCA,得到
。PCA操作的目的就是把它们变换到相应的子空间。同时,把
和
合并成一个数据集
并计算PCA得到
。【此时有三个数据集了。如果两个domain相似度高的话,那么它们距离
的距离应该都会很小。】计算两个domain和
的空间的夹角,这两个角度如果很小的话,表示两个domain距离很小。在避免距离过大的基础上,采用了一种贪心算法:尽可能地取最大的
,取得更多的子空间个数,保留更多数据集的信息。
- 被SVD的矩阵是两个矩阵的乘积(
)。这时候,我们把对角矩阵的每个元素叫做这两个矩阵之间的principal angle,表示它们的距离。
- 针对给定的两个数据集
- 度量domain之间相似度的Rank of Domain指标
学习迁移
《Learning To Transfer》
如何选择迁移学习算法达到最好的效果
从已有的迁移学习方法和结果中学习迁移的经验,然后再把这些学习到的经验应用到新来的数据。类似于增量学习的迁移学习框架
学习迁移的经验
迁移的经验(transfer learning experience):四元组(Se,Te,ae,le),即在一对源域和目标域(Se,Te)迁移任务(从源域转化到目标域)中,从大量算法中选择了某种算法e后,任务效果有多少提升(le)。
基于共同特征空间以及流形集成法
-
像TCA、JDA这种,把源域和目标域映射到一个共同的空间,然后在这个空间中学习一个变换矩阵的方法,就叫做基于共同特征空间;
-
而像GFK这种,把数据映射到流形空间以后,跟走路一样由源域和目标域中间若干个(无数个)点构成的子空间来综合表示迁移过程的,就叫做流形集成法。
-
两种方法的本质目标:学习特征的变换矩阵W(迁移学习的知识,是唯一的),
学习目标
利用MK-MMD,学习所有迁移对最优的,使得平均误差最小的矩阵W。除此之外,作者在学习目标里又加了另一个正则项:要保持源域中的一些信息。
应用到新领域
W是从旧的经验中学到的,对新数据可能效果不好,新的W应该是能在新的数据上更新(类似于增量学习)表现效果最好的那个W。
负迁移
《A survey on transfer learning》 杨强
负迁移指的是,在源域上学习到的知识,对于目标域上的学习产生负面作用。产生原因:源域和目标域不相似(数据分布等);迁移学习方法不合理。
杨强教授团队2015在KDD上发表了传递迁移学习文章《Transitive transfer learning》;2017年AAAI上《Distant domain transfer learning》,可以用人脸来识别飞机。这表明传统迁移学习只有两个领域足够相似才可以完成,而当两个领域不相似时,传递迁移学习却可以利用处于这两个领域之间的若干领域,将知识传递式的完成迁移。
迁移的两种层次
Eric Tzeng发表在ICCV 2015上的文章《Simultaneous Deep Transfer Across Domains and Tasks》
现有的深度迁移学习方法通常都只是考虑domain transfer,而没有考虑到类别之间的信息。如何把domain和task transfer结合起来,是一个问题。
-
domain transfer:就是适配分布,特别地是指适配marginal distribution。如何做domain transfer:在传统深度网路的loss上,再加另一个confusion loss,判断classifier能否将两个domain较好分开。
-
task transfer:就是利用class之间的相似度,其实特指的是conditional distribution。根据source中的类别分布关系(所有样本得到的类别概率加权平均),来对target做相应的约束。
部分迁移学习
Partial Transfer Learning with Selective Adversarial Networks
CVPR 2018接收的文章:《Importance Weighted Adversarial Nets for Partial Domain Adaptation》
源域与目标域的关系
- 源域、目标域的类别空间分别是
和
- 传统迁移学习设定是
- partial transfer(部分迁移学习)中,变成了
。这更符合显示的场景
- 源域和目标域只共享了某一部分类别:ICCV-17的Open set问题
域对抗网路
-
对抗网络可以很好地学习doman-invariant的特征,从而在迁移学习中能发挥很大作用。
-
对抗网络包含两个网络:一个是判别器
(discriminator),它的作用是领域分类器,最大限度地区分source domain和target domain;一个是生成器
(generator),它的作用是特征提取器,提取domain-invariant features,来迷惑判别器。
-
Selective Adversarial Network:约束是样本级别的,可以控制尽可能让更相似的样本参与迁移。类别级别的约束,可以很好地避免不在target domain中的那些类别不参与迁移。
-
由于源域和目标域的类别不同,因此作者提出对它们分别采用不同的特征提取器F进行。在学习时,固定源域的特征提取器不变,只学习目标域的特征。利用领域分类器D筛选源-目标相似的样本,利用D0进行域适配。对源域部分的重要性权重w进行了归一化,以更加明确样本的从属关系。
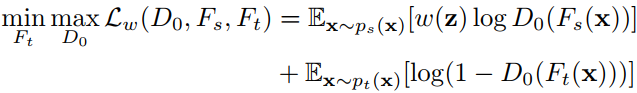
-
《Source-selection-free Transfer Learning》:类似于图嵌入的方法,将源域和目标域的类,用第三方联系,处理成
PxP的 矩阵后降维成m维的向量表示,从而表现类别之间的距离关系。 -
基于条件对抗网络的领域自适应:将特征f和类别g一起做自适应,借鉴数学上的 多线性映射(Multilinear Map) 的概念,用张量乘法
来表征特征和分类器彼此之间的关系。当数据维度太高时,直接从特征里随机采样一些向量做乘法。
在线迁移学习
目标域数据以流式一个一个来时,如何借助已有的源域数据,为目标域构建可依赖的分类器?
任务迁移
CVPR 2018:《Taskonomy: Disentangling Task Transfer Learning》
Domain相同,task不同,也就是
,需要探索这些任务之间的可迁移性。
方法
- 建立计算图,图中的节点表示任务,节点之间的边就表示迁移性,边的权重表示从一个任务迁移到另一个任务的可能表现。此计算图定义任务之间的可迁移性。
- 对不同任务进行建模,然后让它们两两之间进行迁移并获取迁移的表现,形成一个矩阵W。将此矩阵分解后,
到
的迁移表现就是矩阵的第
个特征向量。
异构网络的迁移
ICML-19《Learning What and Where to Transfer》
固定+微调的模式是否是唯一的迁移方法?
如果2个网络结构不同(比如),此时如何做迁移?
-
学习源域网络中哪些层(what)的知识可以迁移多少给目标域的哪些层(where)。
-
学习目标:
,其中
是一个线性变换,
表示目标域网络中第
层的特征表达,
表示预训练好的源域网络中的第
层的特征表达,
是待学习参数集合。
-
从网络较浅的层进行迁移,其结果往往比从较高的层进行迁移具有更小的波动性。