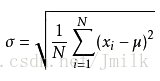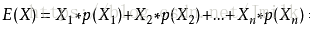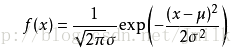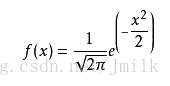前言
首先借机回答一下读者小伙伴的问题,计算原理、组合和排列的现实意义是什么?学习数学对从事 IT 行业而言有什么帮助?
实话说,这些问题应该是普遍存在的,曾经是我的问题,也可能会成为你的问题。欢迎大家在评论区里说说自己的看法。
计数原理:又称基本计数原理,它将实现一个目标的行为抽象成 分步 和 分类 两种,正如计数原理中给出的例子。计数原理通过这两种计数规则为解决现实生活中大多数的计数问题提供了思路和工具。所谓计数,其目的是为了求解出一个「总数」,比如:完成一件事情所拥有的全部做法;达到一个目的所拥有的全部可能。
组合与排列:求解的是 特定集合空间里所拥有的元素之间的组合和排列的可能性,是一个特定条件下的「总数」,所以在组合与排列文中推导公式时就引入了计算原理。组合与排列是概率论中重要的基础,因为其求解的总数,常被作为概率结果中的分母。
至于学习数学对从事 IT 行业有什么实际上的作用?就当下而言,对大数据和人工智能方向的研究很有用,数理基础不扎实容易事倍功半,至于别的研究方向就要各凭兴趣爱好。对未来而言,笔者不相信计算机应用的未来,但相信计算机科学的未来,所以为了以后更好适应行业的发展,需要作出长远准备。
统计与分布
统计和分布的核心在于「描述」,用简明且可操作的方式直观展现大量样本的宏观样态,这是统计与分布所解决的主要问题之一。
使用单一数据定义来概括性描述一些抽象或复杂数据的方式,即为统计学指标。使用指标来描述问题能有效将复杂的问题因素单一化,比如 PM2.5 指标。常见的统计学指标有 加和值、平均值、标准差、中位数、众数 等。
加和值:使用加和值来描述问题最大的好处是直奔主题,忽略个体样本细节。比如超市结账,我们只需要知道总共需要付多少钱,而无须关心每一件商品的价格。
平均值:使用平均值能够对整体样本有一个概括性的描述,同时也能兼具对每个个体样本的描述。比如某个人的成绩是低于还是高于整体平均值。
众数:使用众数能够描述整体样本的偏好特征。比如小明每周要看 5 场电影,其中喜剧看了 3 场,为众数,可以看出小明对喜剧电影的偏好。
中位数:使用中位数能够描述样本的分布特征,在一定程度上可以消除个别极端的个体样本值对整体样本平均值的影响。将样本集中的极端值剔除,然后求得的平均值往往会更加接近中位数。
标准差
使用标准差能够描述个体样本与整体样本平均值之间的差异,差异值越大,表示个体与整体平均线的离散型(正、反差异)越大。
标准差公式:
- 其中 (x - μ)^2 表示个体样本 x 与整体均值的离差,因为离差只能是正数,所以求平方。
可见,标准差是一组数据平均值分散程度的度量。
加权均值
加权平均值是一种特殊的平均值,现实中很多问题的均值结果不仅取决于个体样本标准值的大小,而且还取决于个体样本标准值出现的次数(频数),这些频数同样对最终的结果有着权衡轻重的作用,所以也将频数叫做权重。
例如:一箱什锦糖里混有牛奶糖 1斤 单价 10元、水果糖 2斤 单价 20元、巧克力糖 3斤 单价 30元,那么求解什锦糖应该售卖多少钱一斤?
显然这是一个求均值的问题,但却不能使用普通平均值算法求解,而是应该使用加权平均值算法,因为 3 种糖果在样本集(箱)中的权重是不同的。
- 平均值:
(10+20+30)/6=10元/斤 - 加权平均值:
(10*1+20*2+30*3)/6 约为 23元/斤
加权平均值公式:累加各个体样本标准值与权重的乘积,再除以个体单位数量。
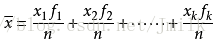
数学期望
数学期望,又称均值,或简称期望,是指在一个随机变量试验中每次可能结果的概率乘以其结果的总和,即累加各个体样本标准值与个体样本概率的乘积。期望描述的是随机变量平均取值的大小。
数学期望公式:
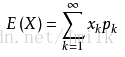
当 Xn(n=1, 2, …, k) 的概率均 1/k 时,数学期望即为平均数。实际上在很多场景中的平均值和期望往往是接近的,但两者又有着区别。
- 平均值:针对的是小量样本集,能够轻易的进行全加和然后再除以单位数。所以得到的结果是准确的,不会有模糊概念。
- 期望:则针对大量样本集,无法轻易实现全加和,只好应用抽样方法。首先得出抽样个体及其出现的概率,然后再加和计算。透过抽样均值,去预测全样本空间的均值,所以称为期望值。
高斯分布
高斯分布,又名正态分布,是一种 概率分布,属概率论学科,对统计学的许多方面都有着非常重要的影响。
概率密度函数:
- f(x) 中的 x 是一个样本特性自变量
- f(x) 则表示拥有样本特性 x 的个体样本数量所占样本总数的比例
- exp 指的是自然常数 e 的幂函数
- σ 表示标准差,σ^2 则为方差
- μ 表示平均值或数学期望
当 μ=0, σ=1 时,为标准正态分布,x 为 0 时得峰值:
正态分布曲线,又称钟型曲线:
正态分布特性:
1. x=μ 时,得到曲线峰值
2. 以 x=μ 为中轴左右对称
3. 属于 [μ-σ, μ+σ] 区间的样本特性的样本数量比例为 68.2%
4. 属于 [μ-2σ, μ+2σ] 区间的样本特性的样本数量比例为 95.4%
5. 属于 [μ-3σ, μ+3σ] 区间的样本特性的样本数量比例为 99.6%
6. μ 越大曲线中轴就越向右移,反之向左
7. σ 越大曲线坡度就越扁平,反之陡峭
应用场景:
假如得知某高校男学生 1000 人,并且以及通过统计计算得出 μ=175,σ=10,那么我们就可以轻易通过高斯密度曲线得出下述结果。
- 身高 165~175 大约 341 人
- 身高 155-165 大约 136 人
- 身高 145-155 大约 21 人
总的来说高斯分布的适用场景有着一个共同特点 —— 一般般的很多,极端的很少。例如,智商很高或很低的人很少,智商一般般的人很多;非常有钱和非常贫穷的人很少,一般般有钱的人很多。可见高斯分布的适用面是极其广泛的,他能够非常简明的将各个区间的概率密度呈现出现。