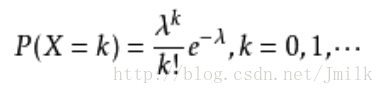目录
前文列表
泊松分布
泊松分布(Poisson)是一种统计与概率学中常见的离散概率分布,适合用于描述单位时间(单位面积)内随机事件发生的次数(个数),例如:一分钟内不断抛硬币并得到正面向上的次数为 30 次,求解得到正面向上次数为 50 次的概率是多少。
概率密度函数:
- λ 表示单位时间(单位面积)内随机事件的平均发生率
- k! 表示 k 的阶乘并且 k 取非负整数
适合于泊松分布的事件需要满足下述 3 个条件:
1. 这个事件是一个小概率事件。
2. 事件的每次发生都是独立的。
3. 事件的概率是稳定的。
例子:公交车站有很多不同线路的公交车,平均每 5 分钟会来两辆公交车,求解 5 分钟内来 5 辆公交车的概率有多大?
解析:在这里问题里,随机事件(公交车来到)拥有固定的平均概率(每 5 钟 2 辆),每次事件随机且独立(不同的线路),所以这个随机事件在单位时间(5 分钟)内出现的次数就近似的服从语泊松分布。
最终代入公式求解得:P(X=k=5) = (2^5 / 5!) * e^(-2) 概率约为 0.0361
除此之外,一放射性源放射出的 alfa 粒子数,某电话交换台收到的电话呼叫数,到某机场降落的飞机数,一个售货员接待的顾客数,一台纺纱机的断头数,都服从泊松分布。
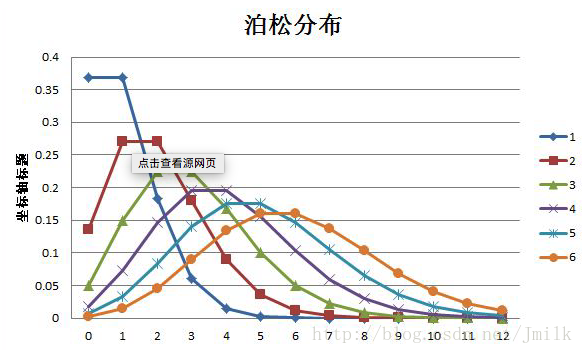
泊松部分函数密度(累积函数)曲线:
分布曲线特点:
- 当 k 小于 λ 时,k 每增加 1 累积概率增速会逐渐加大
- 而当 k 大于 λ 后,累积概率的降速也会逐渐加大。
为什么说现实生活多数服从泊松分布?
假定一个事件在一段时间内随机发生,且符合以下条件:
(1)将该时间段无限分隔成若干个小的时间段,在这个接近于零的小时间段里,该事件发生一次的概率与这个极小时间段的长度成正比。
(2)在每一个极小时间段内,该事件发生两次及以上的概率恒等于零。
(3)该事件在不同的小时间段里,发生与否相互独立。 则该事件称为 Poisson Process。医院的例子,如果把一天分成 24 个小时,或 24*60 分,或 24*3600
秒。时间区间越分越短,该区间内来病人的概率就越小(比如医院在 12 点到 12 点又一毫秒之间来病人的概率是不是很接近于零?),符合条件(1);另外如果我们把时间分的很细很细,是不是同时来两个病人(或者两个以上的病人)就是不可能的事件?符合条件(2);条件(3)的要求则比较苛刻,要求病人们来医院的概率必须是相互独立的,如果不然,则事件不能看作是泊松分布。
所以,简单来说,大多数现实生活中的例子中如果事件是相互独立的,那么它就很可能是符合泊松分布的。摘自知乎:楚小鱼