前一段时间师姐在看大话数据结构这本书,当看到堆排序时她问我,当时我觉得堆排序很简单,无非就是堆顶和堆尾对换,并输出最后一个,剩下的进行堆调整再一次次循环下去。但是她又问道怎么实现堆调整,当时有点路子,但是当我真正想实现的时候,却出现了很多问题,正好最近正在写一些排序算法,所以今天就详细说说堆排序的具体。
堆:
堆是一个完全二叉树,分有最大堆和最小堆;它的每个节点值总比每个孩子值都大(这是最大堆,最小堆反之,下面提到得堆均为最大堆),并且最后一层处于左侧。
下面我们说说初始化堆:利用数组实现
如下图所示,我们先把数组{1,2,3,5,2,3}化为一个完全二叉树(堆),然后在对其进行堆调整,这里我们只谈最大堆,所以我们可以利用每个节点值总比每个孩子值都大这个性质来进行调整。

下面给出初始化堆的代码:
void max_HeapAdjust(int* A, int index, int n) { //最大堆 if (2 * index < n){ //这个条件可以跳出递归 int cur = index; //用cur来记录结点值和孩子值比较大的那个值得下标 if (2 * index + 1 < n && A[2 * index + 1] > A[cur]) //我当时用了index,不好实现,虽然测试过了几个例子,但是还是用来记录比较好 cur = 2 * index + 1; if (2 * index + 2 < n && A[2 * index + 2] > A[cur]) cur = 2 * index + 2; if (cur != index){ swap(A[cur], A[index]); //孩子大的那个与结点互换。 max_HeapAdjust(A, cur, n); } } } //从 n / 2 - 1 往前循环是因为从这个值开始往后面就没有子节点了,我们这里只考虑有孩子的。 int* bulitHeap(int* A, int n) { for (int i = n / 2 - 1 ; i >= 0; i--) max_HeapAdjust(A, i, n);return A; }
我用了上图的中数组进行了测试,显示正确。
接下来我们就进入了堆排序的实现了,我们还是以上面那个{1,2,3,5,2,3}的例子来实现。
首先我们谈谈堆排序的思想:将待排序的序列转化成为一个堆;此时将堆顶的元素与堆尾的元素交换,并且输出对换后堆尾的数据,并将其移除;然后将剩余的n-1序列进行调整之后再首尾对调输出移除,如此反复下去。知道只有一个节点,直接将其输出。
在实现过程中我们把交换之后的元素放在数组的尾部,并且对剩下n-1个元素进行调整在交换,剩下n-2个。。。如此反复下去。
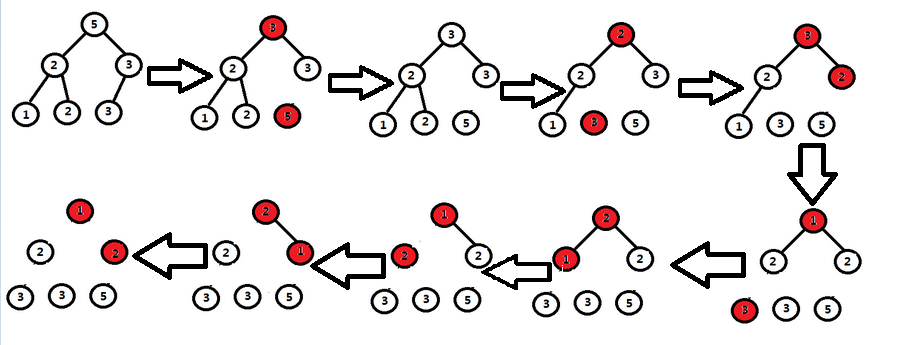
经过上面的变化过程我们可以发现,我们在给一个有序堆进行调整的时候,应该不用在进行一些循环建堆的过程,我们只需要进行上面代码中的一次max_HeapAdjust调整即可,因为堆除了堆顶其他都是有序的,那么我们只有一条线走到底调整即可。
下面给出测试的完整代码:
#include<iostream> using namespace std; void swap(int& a, int& b) { int temp = a; a = b; b = temp; } //堆调整算法实现 void max_HeapAdjust(int* A, int index, int n) { if (2 * index < n){ int cur = index; if (2 * index + 1 < n && A[2 * index + 1] > A[cur]) cur = 2 * index + 1; if (2 * index + 2 < n && A[2 * index + 2] > A[cur]) cur = 2 * index + 2; if (cur != index){ swap(A[cur], A[index]); max_HeapAdjust(A, cur, n); } } } int* heapSort(int* A, int n) { for (int i = n / 2 -1 ; i >= 0; i--) //该循环建堆 max_HeapAdjust(A, i, n); for (int j = n -1 ; j > 0; j--) { swap(A[j], A[0]); max_HeapAdjust(A, 0, j); //堆调整 } return A; } int main() { const int n = 6; int a[n] = { 1, 2, 3, 5, 2, 3 }; for (int i = 0; i != n; ++i) cout << a[i] << " "; cout << endl; heapSort(a, n); for (int i = 0; i != n; ++i) cout << a[i] << " "; cout << endl; return 0; }
堆排序在排序算法中的效果还是很好的,所以还是自己实现出来比较好。
声明:本篇文章参考了<<大话数据结构>>以及牛客网上的一些思路。